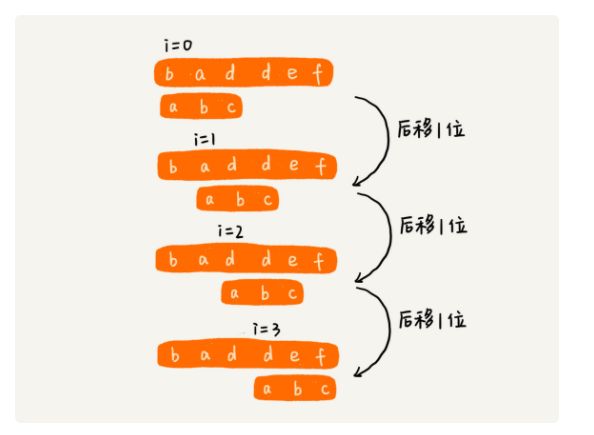
BF算法(Brute Force)
暴力匹配算法,在主串和模式串每次比较都只前进一个位置,进行比较。
code
public class BF {
public static void main(String[] args) {
String a = "aaabbaaaccssdd";
String b = "acc";
System.out.println(bfFind(a, b, 3));
}
public static int bfFind(String S, String T, int pos) {
char[] arr1 = S.toCharArray();
char[] arr2 = T.toCharArray();
int i = pos;
int j = 0;
while(i < arr1.length && j < arr2.length) {
if(arr1[i] == arr2[j]) {
i++;
j++;
}
else {
i = i - j + 1;
j = 0;
}
}
if(j == arr2.length) return i - j;
else return -1;
}
}
时间复杂度
假设源字符串长度为m,目标字符串长度为n,则:
最好情况下是第一轮就成功匹配,则时间复杂度为O(n);
最坏情况下是遍历到最后才成功匹配,或者遍历到最后发现匹配不成功,则时间复杂度为O(n(m-n+1)),一般实际使用时m >> n,所以可以认为趋近于O(mn);
RK 算法
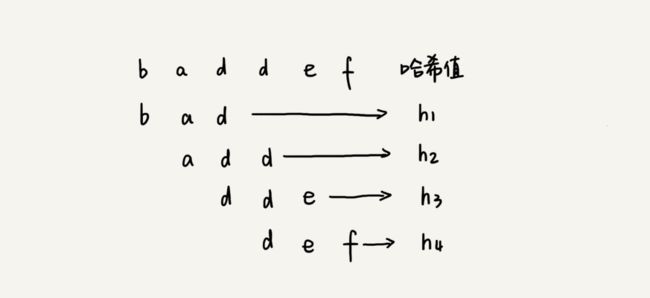
RK 算法的全称叫 Rabin-Karp 算法,通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了(这里先不考虑哈希冲突的问题,后面我们会讲到)。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串比较的效率就提高了。
时间复杂度
O(n)
notice:
但是这种算法,需要每个子串求哈希值,并且需要解决哈希冲突的问题,哈希算法的冲突概率要相对控制得低一些,如果存在大量冲突,就会导致 RK 算法的时间复杂度退化,效率下降。极端情况下,如果存在大量的冲突,每次都要再对比子串和模式串本身,那时间复杂度就会退化成 O(n*m)。但是大多数情况下,冲突不会很多,RK算法效率会高于BF算法的效率。
KMP算法
KMP核心思想
在模式串与主串匹配的过程中,当遇到不可匹配(失配)的字符的时候,找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况。
KMP实现的思路
先构建模式串的next数组,模式串中如果失配元素索引为x,模式串跳过next[x-1]个索引,从而达到减少模式串比较次数的目的。
KMP算法的元素
最长可匹配的前缀子串,最长可匹配的后缀子串
这两个概念是对应的,即模式串中从第一个元素开始算起,和后缀元素从最后一个元素算起,最多前k位索引和后k位索引字符串完全一致。
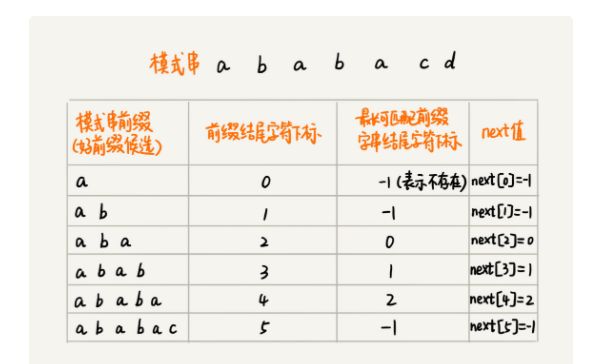
next[x]数组
表示在模式串中从0-x位索引构成的字符串,最大的可匹配子串。
例子
在 S[0] 尝试匹配,失配于 S[3] <=> P[3] 之后,我们直接把模式串往右移了两位,让 S[3] 对准 P[1]. 接着继续匹配,失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位,把 S[8] 对准 P[3]. 此后继续匹配直到成功。
code
// a, b分别是主串和模式串;n, m分别是主串和模式串的长度。
public static int kmp(char[] a, int n, char[] b, int m) {
int[] next = getNexts(b, m);
//模式串的索引
int j = 0;
for (int i = 0; i < n; ++i) {
//发现失配项,在模式串中找到可以继续匹配的最大模式子串
while (j > 0 && a[i] != b[j]) { // 一直找到a[i]和b[j]
//寻找此时模式串的最大匹配子串,让j指向最大匹配子串的下一个索引
j = next[j - 1] + 1;
}
//遇到匹配的元素,k++,模式串向前移动
if (a[i] == b[j]) {
++j;
}
//找到主串中,匹配模式串的其实索引
if (j == m) {
return i - m + 1;
}
}
return -1;
}
失效函数计算方式
快速构建next数组,其核心就是:“模式串自己和自己做匹配”。
每次寻找next[x],将模式串分为两段,一段为模式串,一段为主串,套用KMP思想构建数组。
notice:
前缀子串一定是包含第一个元素的字符串
后缀子串一定是包含最后一个元素的字符串
k=next[x]表示
在P[0]~P[x] 这一段字符串中,使得k-前缀恰等于k-后缀的最大的k。
即在p[0]到p[x]这一段字符串中,最大的可匹配子串是k(前k个元素和后k个元素相等)。
求k的两种情况
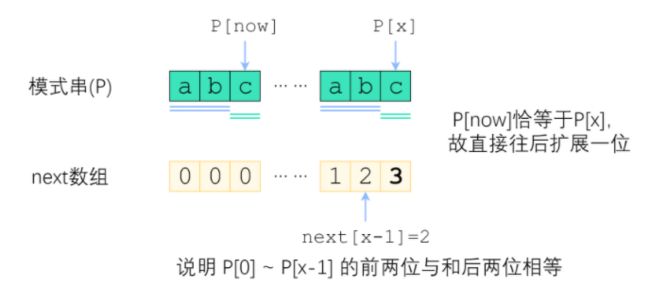
1.p[now]=p[x]
k表示p[0]-p[x-1]中,最大的匹配长度,如果此时p[now]==p[x],正好说明前k+1和后k+1相等(k+1前缀和k+1后缀相等)则next[x]=k+1。
2.p[now]!=p[x]
当p[now]!=p[x]的时候
说明此时next[x]!=k+1(k表示其前一个索引位的最长匹配长度),此时不匹配项是p[now]和p[x],那么此时如果存在最长匹配子串,那其一定是在子串A中寻找,而子串A中的最长匹配子串是next[now-1],所以此时now=next[now-1],用此时的最长匹配子串的下一位和p[x]比较,即p[next[now-1]+1] == p[x],如果相等,则找到此时的最长匹配子串,即k=next[now-1]+1,如果没找到则继续缩小now的范围,在其中寻找最小匹配子串,直到k=-1(k=-1表示没有匹配项)。
code
getNexts
// b表示模式串,m表示模式串的长度
private static int[] getNexts(char[] b, int m) {
int[] next = new int[m];
next[0] = -1;
int k = -1;
for (int i = 1; i < m; ++i) {
//情况2 p[now]!=p[x] 寻找此时的最长可匹配子串
while (k != -1 && b[k + 1] != b[i]) {
k = next[k];
}
if (b[k + 1] == b[i]) {
++k;
}
next[i] = k;
}
return next;
}
时间复杂度
O(m+n)
分析过程
KMP算法实现主要分为两部分
1.分析next数组的时间复杂度
getNexts中循环次数最多的两个代码块是for循环和while循环,第一层for循环i 从 1 开始一直增加到 m,而 k 并不是每次 for 循环都会增加,而 while 循环里 k=next[k],实际上是在减小 k 的值,k 累积都没有增加超过 m,所以 while 循环里面 k=next[k]总的执行次数也不可能超过 m。因此,next 数组计算的时间复杂度是 O(m)。
2.分析kmp时间复杂度
i 从 0 循环增长到 n-1,j 的增长量不可能超过 i,所以肯定小于 n。而 while 循环中的那条语句 j=next[j-1]+1,不会让 j 增长的,那有没有可能让 j 不变呢?也没有可能。因为 next[j-1]的值肯定小于 j-1,所以 while 循环中的这条语句实际上也是在让 j 的值减少。而 j 总共增长的量都不会超过 n,那减少的量也不可能超过 n,所以 while 循环中的这条语句总的执行次数也不会超过 n,所以这部分的时间复杂度是 O(n)
综上
KMP 算法的时间复杂度就是 O(m+n)。