OmicStudio又双叒叕上新啦,这次上线的是 【相关性热图】。熟悉云平台的用户知道,我们已经有了 【相关性系数图】 云工具了,为什么还要再上线一个相关性的云工具呢:
1.这个云工具与联川微生物组学结果中的相关性分析结果一致,做了微生物组的用户可以直接用您的数据重现分析结果;
2.原相关性系数图只能计算单张表格的相关性,即表中数据间的相关性,此云工具不仅可以计算表内的,还可以计算表间数据的相关性;
3.这款云工具提供了更多细致的功能,如更换数据处理和筛选方式、调整配色方案、增加图例注释和聚类等高级功能,另外基础调图参数也更丰富了(如下图);
4.原相关性系数图中显示的是相关性数值,此工具默认显示的是p值的显著性符号,即一张图中既体现了R值(相关性值,用颜色表示),又体现了P值(R值结果的显著性,用符号表示),信息呈现的维度更为丰富了;
5.完善了说明资料:点击页面中的紫色问号(如下图)即可查看先关模块的说明,本文以下内容均来自此处。
云工具除了微生物组,其他组学可用么?
可用。相关性分析的原理都是一致的,只要您的数据符合计算相关性的应用场景即可使用。
这个云工具的应用场景是什么?
此云工具可以计算两张表数据间的相关性,也可以计算一张表内数据的相关性。依据您想观察的对象(X与X的相关,X与Y的相关)来决定如何输入数据。
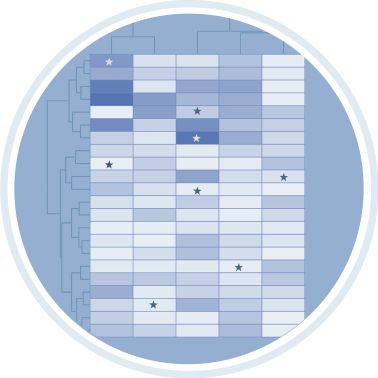
如示例数据,观察的是菌群丰度(1) 和环境因子间(2) 的相关性,图片的行列分别与两张数据表对应。
如下图,是分析单张表 的结果示例,数据用的是上述的菌群丰度(1),可以看到这张图的结果与原相关性系数云工具的分析结果接近,行列名是相同,观察的是表内数据的相关性。
图片如何解读?
图中颜色越深代表相关关系越强,相关关系有两种:强相关和负相关,一般用暖色系代表正相关,冷色系代表负相关。星号标记代表相关性值的显著性,依据显著性不同再细分符号,一般星号越多显著性越大。如果一个方法颜色较深(相关性强),显著性也强(相关性值的计算结果在统计学意义上更可靠),那么我们认为这个格子对应的横纵坐标对象之间有强烈的相关关系。对于单表来说,图片是斜对角对称的,且对角线数字恒为1(自己和自己的相关性为100%)。
通过这个分析我可以得到什么?
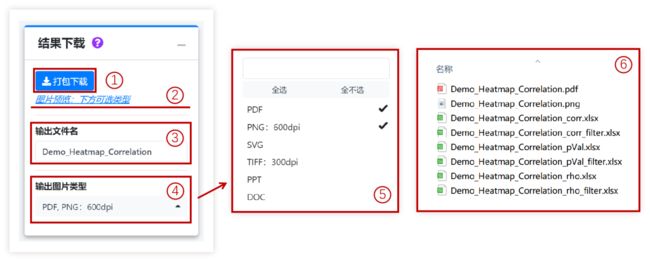
如上右图(6)为相关性分析结果表格和图片,共6张表格(也可能是3张,见下文输出表格说明)和至少1张图片(图片张数由您选择的图片格式类型决定(4))。
如何进行数据处理和筛选?
(1)相关性计算方法:本工具提供两种相关性计算方法:spearman(斯皮尔曼)和pearson(皮尔逊)【1】【2】。
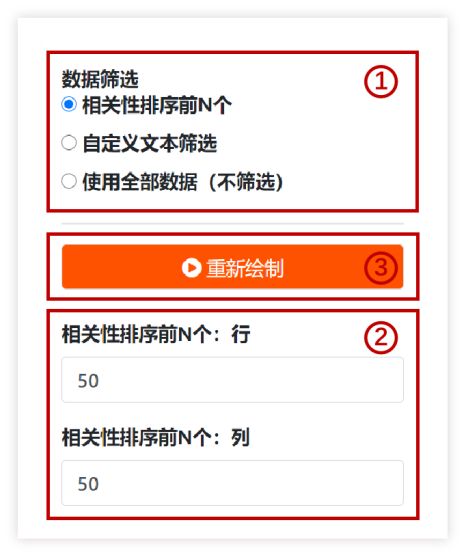
(2)数据筛选:本工具提供两种数据筛选方式:相关性排序前N个;自定义文本筛选。若选择这两种筛选方式任意一种,分析结果中会出现带filter后缀的表格文件,您可在这些表格中查看您筛选后的数据。若数据较多,建议进行筛选后再绘图以清晰地在图中呈现p值显著性或相关性数值。
相关性排序前N个:选择这个选项后,出现新的选项(2),参数修改完成后需点击【重新绘图】按钮(3)。相关性排序前N个的定义是:对行(或列)的相关性绝对值总和进行排序,取前N个。这是一种快速的选择方式,如果您关注的对象不在其中,可以选择“自定义文本筛选”,见下文。
自定义文本筛选:这种方式更适合剔除数据,若想大量指定需要呈现的数据,建议在上传文件前就整理好需要呈现的对象。
(1)选择这个选项后,图片区域悬浮框出现新的选项(2);
(2)此处可以分别调整行和列的呈现对象,若您的数据名称较长,界面可能不够宽敞,点击(3)可放大此界面,如右图;
(4)点击(2)中控件出现此界面:搜索框可以直接查找您关注的对象,点击“全选”或“全不选”按钮可以实现快速选择,“√”意味着被选择,点击即可选择或取消;
(5)修改完参数后,需点击此按钮。
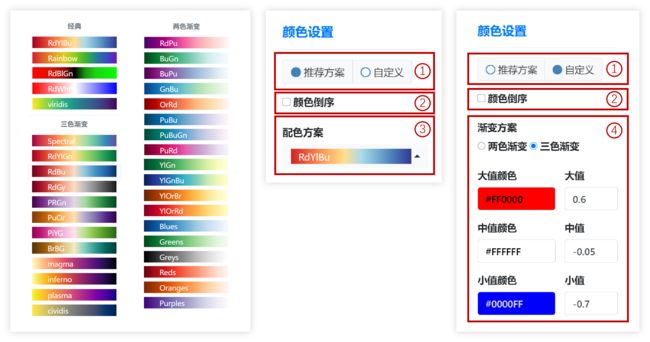
如何调整配色方案?
(1)云平台精炼了一些配色方案供您挑选,当然,若有特殊数据需求,您也可以自定义配色方案;
(2)将您选择的设置的颜色顺序翻转;
(3)云平台的配色方案已罗列在左测,主要分为三个部分:“经典”是常用的配色方案,推荐使用;“三色渐变”适合表达相关性系数,绝对值越大颜色越深;“两色渐变”一般适用单向变化的数据;
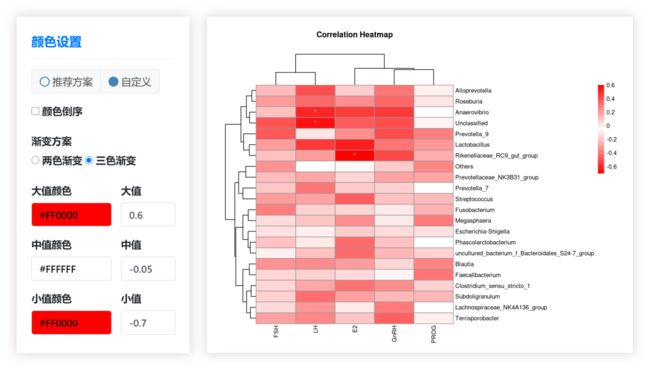
(4)您可以自定义设置配色方案,除了定义颜色外,还可以调整颜色的分布:一般来说,三个颜色分别对应您数据的最大值、中值和最小值,您也可以调整此值以设置非均匀的配色方案。另:颜色设置方式除了点选,也可以填值,所填值可以是十六进制,也可以是rgb形式。若您填写的最大值小于您数据的最大值,则超过此值的数据均使用设定的最大值所对应的颜色;“小值”以此类推。
如何只以相关性强度来配色(不分正负)?
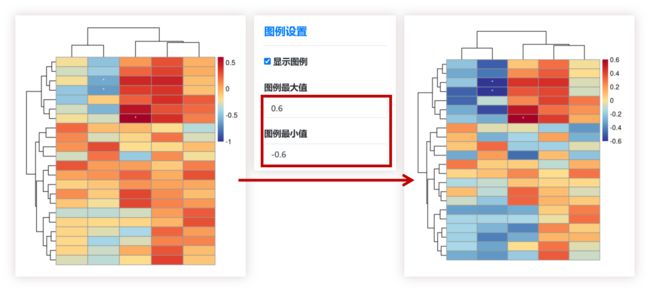
图例范围不对称,如何调整?
如何进行分组注释(增加彩条)?
分组注释功能可用于绘制如上图的效果,用彩条代表样本(或物种、环境因素等)分类。
参考文献:
【1】D. J. Best & D. E. Roberts (1975). Algorithm AS 89: The Upper Tail Probabilities of Spearman's rho. Applied Statistics, 24, 377–379. doi: 10.2307/2347111.
【2】Myles Hollander & Douglas A. Wolfe (1973), Nonparametric Statistical Methods. New York: John Wiley & Sons. Pages 185–194 (Kendall and Spearman tests).