遗传算法(Genetic Algorithm)从了解到实例运用（上）（python）

 

---

前言

本文主要介绍了数学建模常用模型遗传算法，从原理出发到编程实现再到实例运用。笔者参与过大大小小五次数学建模，个人觉得该优化算法值得一学。

---

提示：以下是本篇文章正文内容

一、遗传算法由来

遗传算法的起源可追溯到20世纪60年代初期。1967年,美国密歇根大学J. Holland教授的学生 Bagley在他的博士论文中首次提出了遗传算法这一术语,并讨论了遗传算法在博弈中的应用,但早期研究缺乏带有指导性的理论和计算工具的开拓。1975年, J. Holland等提出了对遗传算法理论研究极为重要的模式理论,出版了专著《自然系统和人工系统的适配》,在书中系统阐述了遗传算法的基本理论和方法,推动了遗传算法的发展。20世纪80年代后,遗传算法进入兴盛发展时期，被广泛应用于自动控制、生产计划、图像处理、机器人等研究领域。

二、遗传算法定义

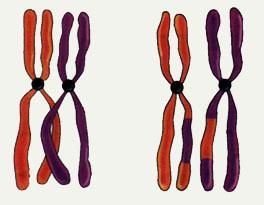
遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。

其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。

遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。

 

三、算法理解

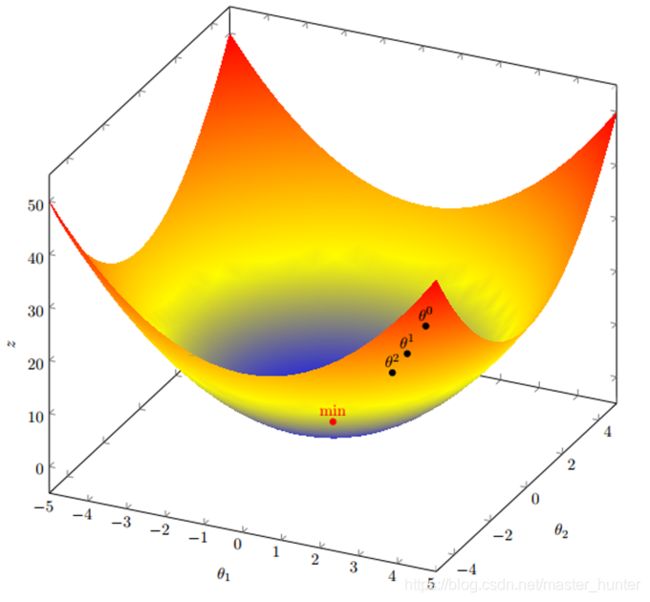
该算法本质上是让我们得到在种群中获得基因最好的个体。这有点类似我之前的博文介绍梯度上升和梯度下降算法中获得最优参数。总的来说就像我们高中时做的求该函数的极大值点，我们往往是运用求导的方式来得到该函数的导函数为0的时候所得到的值，从而代入原方程求出极大值。而这些优化算法只不过是把函数、求导方式方法用其他东西替换了而已，本质上还是差不多的。

图为梯度下降：

既然我们把函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一登山者，我们希望这些登山者能够爬上高峰。所以求最大值的过程就转化成一个“爬山”的过程。

1. 梯度上升算法：

      我们总是往向着山顶的方向攀爬，当爬到一定角度以后也会驻足停留下观察自身角度是否是朝着山顶的角度上攀爬（从搜索空间中随机产生邻近的点，从中选择对应解最优的个体，替换原来的个体，不断重复上述过程。）。并且我们需要总是指向攀爬速度最快的方向爬。但是这座山不一定是最高峰，只能达到局部最优解而不是全局。

2. 模拟退火：

     我们爬山坡的时候突然发现登山指明方向的工具失灵了，不清楚我们需要爬的最高山峰是哪座。导致我们不得不在这这篇山谷不停探索，这是我们可能走向平地或者继续爬山峰，然后我们试图爬上山峰后，继续向全体更高的山峰探索，最后我们逐渐向目标最高的山峰爬去。（这个方法来自金属热加工过程的启发。在金属热加工过程中，当金属的温度超过它的熔点（Melting Point）时，原子就会激烈地随机运动。与所有的其它的物理系统相类似，原子的这种运动趋向于寻找其能量的极小状态。在这个能量的变迁过程中，开始时，温度非常高， 使得原子具有很高的能量。随着温度不断降低，金属逐渐冷却，金属中的原子的能量就越来越小，最后达到所有可能的最低点。利用模拟退火的时候，让算法从较大的跳跃开始，使到它有足够的“能量”逃离可能“路过”的局部最优解而不至于限制在其中，当它停在全局最优解附近的时候，逐渐的减小跳跃量，以便使其“落脚 ”到全局最优解上。）

3. 遗传算法：

    这次登山比赛中邀请了很多登山者，我们随机降落到了这片山脉各处。但是我们并没有收到具体要爬向哪座山峰只能随机攀爬。但是每过一段时间举办方就将一些还没有准备爬的和爬的还不够高的登山者给淘汰掉。随着比赛的进行将会有越来越多的登山者被淘汰掉，而越是接近山峰的登山者就越有可能获胜。于是经历了多天的比赛，剩下的登山者都基本聚集在一个山峰附近，他们交换自己的情报和装备，一起朝着胜利的方向进行。（  模拟物竞天择的生物进化过程，通过维护一个潜在解的群体执行了多方向的搜索，并支持这些方向上的信息构成和交换。是以面为单位的搜索，比以点为单位的搜索，更能发现全局最优解。）

四、遗传算法的特点和应用

遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法，与传统的优化算法相比，具有以下特点：

1. 以决策变量的编码作为运算对象。

遗传算法是使用决策变量的某种形式的编码作为运算对象。这种对决策变量的编码处理方式，使得我们在优化计算中可借鉴生物学中染色体和基因等概念，可以模仿自然界中生物的遗传和进化激励，也可以很方便地应用遗传操作算子。

2. 直接以适应度作为搜索信息。

遗传算法仅使用由目标函数值变换来的适应度函数值就可确定进一步的搜索范围，无需目标函数的导数值等其他辅助信息。直接利用目标函数值或个体适应度值也可以将搜索范围集中到适应度较高部分的搜索空间中，从而提高搜索效率。

3. 使用多个点的搜索信息，具有隐含并行性。

遗传算法从由很多个体组成的初始种群开始最优解的搜索过程，而不是从单个个体开始搜索。对初始群体进行的、选择、交叉、变异等运算，产生出新一代群体，其中包括了许多群体信息。这些信息可以避免搜索一些不必要的点，从而避免陷入局部最优，逐步逼近全局最优解。

综上，由于遗传算法的整体搜索策略和优化搜索方式在计算时不依赖于梯度信息或其他辅助知识，只需要求解影响搜索方向的目标函数和相应的适应度函数，所以遗传算法提供了一种求解复杂系统问题的通用框架。它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于各种领域，包括：

• 函数优化
• 组合优化生产调度问题
• 自动控制
• 机器人学
• 图像处理
• 人工生命
• 遗传编程
• 机器学习
   

五、算法实现过程

我们可以从该算法具体实现步骤结合你想要达到的目的来了解该算法需要做些什么。

就以爬山比赛为例，如果我们作为爬山比赛的举办方，该如何设定合理的：

1.建立表现型和基因型的映射关系

我们需要识别每个登山比赛者的定位，就必须给他们设定相对应的编码。

2.随机初始化种群，个体为该种群的数字化编码

比赛开始，开始随机投放一批参赛选手降落到山脉地区。

3.解码获得个体对应的数值信息

比赛进行到一段时间开始统计每个参赛选手的进度状态。

4.用适应性函数对每一个基因个体作一次适应度评估

通过举办方邀请的专家进行评分，爬的最高的登山者得分最高。

5.选择阶段的理念就是选出最适合的个体，让它们将基因传递给下一代。

每隔一段时间，淘汰一批得分不理想的选手。

6.交叉运算时遗传算法中最重要的阶段。对于每一对即将结合的父体，算法在基因中随机选择一个交叉点交换它们的某些基因，产生新的基因组合，期望将有益基因组合在一起。

其余的登山选手互相交换信息和装备。

7.在形成的新后代中，它们的一些基因会以较低的随机概率出现变异，也就是说字符串中的一些比特会发生变动。

可能信息和装备产生了某些变化导致爬山的方向发生改变。

8.如果种群出现了收敛（不再生成和之前几代有巨大差异的后代），遗传算法就会终止。

比赛接近尾声，余下的登山者几乎都在目标山顶的附近。

以上就是整个遗传算法的流程。

通常认为遗传算法有5个阶段：

• 初始种群
• 适应度函数
• 选择运算
• 交叉运算
• 变异运算

遗传算法的伪代码可以写为：

1. 起始
2. 形成初始种群
3. 计算适应度
4. 重复
5. 选择运算
6. 交叉运算
7. 变异运算
8. 计算适应度
9. 直到种群出现收敛
10. 终止

六、具体实现方法

基本遗传算法（SGA）由编码、适应度函数、遗传算子（选择、交叉、变异）及运行参数组成。

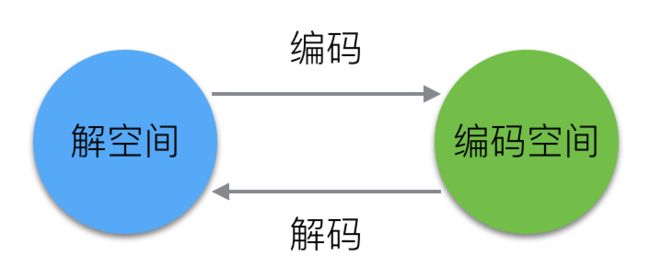
1.编码与解码

实现遗传算法的第一步就是明确对求解问题的编码和解码方式。

对于函数优化问题，一般有两种编码方式，各具优缺点

• 实数编码：直接用实数表示基因，容易理解且不需要解码过程，但容易过早收敛，从而陷入局部最优。例如坐标（1,2），（2,3）。
• 二进制编码：稳定性高，种群多样性大，但需要的存储空间大，需要解码且难以理解。如：1110001010111

• 浮点编码法：适用于在遗传算法中表示范围较大的数，适用于精度要求较高的遗传算法，改善了遗传算法的计算复杂性，提高了运算交率。但存储空间大，解码且难以理解。如：1.2-3.2-5.3-7.2-1.4-9.7

• 符号编码法：符合有意义积术块编码原则，便于在遗传算法中利用所求解问题的专门知识，便于遗传算法与相关近似算法之间的混合使用。

在上面介绍了一系列编码方式以后，那么，如何利用上面的编码来为我们的袋鼠染色体编码呢？首先我们要明确一点：编码无非就是建立从基因型到表现型的映射关系。这里的表现型可以理解为个体特征（比如身高、体重、装备等等）。

那么，在此问题下，我们关心的个体特征就是：登山者的位置坐标（因为我们要把高低低的登山者给淘汰掉）。我们关心的始终是登山者在哪里，并且只要知道了登山者的位置坐标（位置坐标就是相应的染色体编码，可以通过解码得出），我们就可以：

1. 在地图上找到相应的位置坐标，算出高度。（相当于通过自变量求得适应函数的值）然后判读该不该淘汰该登山者。
2. 可以知道交换情报和装备（染色体交叉和变异）后登山者新的位置坐标。

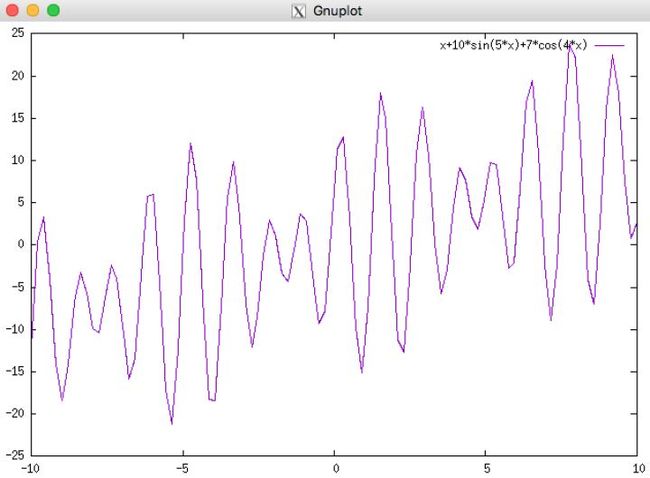
以我们的目标函数 f(x) = x + 10sin(5x) + 7cos(4x), x∈[0,9] 为例。（该例子转载为知乎）

假如设定求解的精度为小数点后4位，可以将x的解空间划分为 (9-0)×(1e+4)=90000个等分。

2^16<90000<2^17，需要17位二进制数来表示这些解。换句话说，一个解的编码就是一个17位的二进制串。

一开始，这些二进制串是随机生成的。一个这样的二进制串代表一条染色体串，这里染色体串的长度为17。

对于任何一条这样的染色体chromosome，如何将它复原(解码)到[0,9]这个区间中的数值呢？

对于本问题，我们可以采用以下公式来解码：

 

x = 0 + decimal(chromosome)×(9-0)/(2^17-1)

 

decimal( ): 将二进制数转化为十进制数

一般化解码公式：

f(x), x∈[lower_bound, upper_bound]
x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)

lower_bound: 函数定义域的下限
upper_bound: 函数定义域的上限
chromosome_size: 染色体的长度

通过上述公式，我们就可以成功地将二进制染色体串解码成[0,9]区间中的十进制实数解。

2.适应度与选择

1.适应度函数（fitness function）

遗传算法中，一个个体(解)的好坏用适应度函数值来评价，在上个问题中，f(x)就是适应度函数。

适应度函数也称评价函数，是根据目标函数确定的用于区分群体中个体好坏的标准。适应度函数总是非负的，而目标函数可能有正有负，故需要在目标函数与适应度函数之间进行变换。

评价个体适应度的一般过程为：

1. 对个体编码串进行解码处理后，可得到个体的表现型。

2. 由个体的表现型可计算出对应个体的目标函数值。

3. 根据最优化问题的类型，由目标函数值按一定的转换规则求出个体的适应度。

适应度函数是遗传算法进化的驱动力，也是进行自然选择的唯一标准，它的设计应结合求解问题本身的要求而定。

2.选择函数（selection）

我们希望有这样一个种群，它所包含的个体所对应的函数值都很接近于f(x)在[0,9]上的最大值，但是这个种群一开始可能不那么优秀，因为个体的染色体串是随机生成的。

如何让种群变得优秀呢？不断的进化。

每一次进化都尽可能保留种群中的优秀个体，淘汰掉不理想的个体，并且在优秀个体之间进行染色体交叉，有些个体还可能出现变异。种群的每一次进化，都会产生一个最优个体。种群所有世代的最优个体，可能就是函数f(x)最大值对应的定义域中的点。如果种群无休止地进化，那总能找到最好的解。但实际上，我们的时间有限，通常在得到一个看上去不错的解时，便终止了进化。

对于给定的种群，如何赋予它进化的能力呢？

• 首先是选择(selection)
  • 选择操作是从前代种群中选择***多对***较优个体，一对较优个体称之为一对父母，让父母们将它们的基因传递到下一代，直到下一代个体数量达到种群数量上限
  • 在选择操作前，将种群中个体按照适应度从小到大进行排列
  • 采用轮盘赌选择方法（当然还有很多别的选择方法），各个个体被选中的概率与其适应度函数值大小成正比
  • 轮盘赌选择方法具有随机性，在选择的过程中可能会丢掉较好的个体，所以可以使用精英机制，将前代最优个体直接选择

下面介绍几种常用的选择算子：（选择算子）

1. 轮盘赌选择（Roulette Wheel Selection）：是一种回放式随机采样方法。每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例。选择误差较大。

2. 随机竞争选择（Stochastic Tournament）：每次按轮盘赌选择一对个体，然后让这两个个体进行竞争，适应度高的被选中，如此反复，直到选满为止。

3. 最佳保留选择：首先按轮盘赌选择方法执行遗传算法的选择操作，然后将当前群体中适应度最高的个体结构完整地复制到下一代群体中。

4. 无回放随机选择（也叫期望值选择Excepted Value Selection）：根据每个个体在下一代群体中的生存期望来进行随机选择运算。方法如下:

   （1） 计算群体中每个个体在下一代群体中的生存期望数目N。

   （2） 若某一个体被选中参与交叉运算，则它在下一代中的生存期望数目减去0.5，若某一个体未 被选中参与交叉运算，则它在下一代中的生存期望数目减去1.0。

   （3） 随着选择过程的进行，若某一个体的生存期望数目小于0时，则该个体就不再有机会被选中。

5. 确定式选择：按照一种确定的方式来进行选择操作。具体操作过程如下：

   （1） 计算群体中各个个体在下一代群体中的期望生存数目N。

   （2） 用N的整数部分确定各个对应个体在下一代群体中的生存数目。

   （3） 用N的小数部分对个体进行降序排列，顺序取前M个个体加入到下一代群体中。至此可完全确定出下一代群体中Ｍ个个体。

6. 无回放余数随机选择：可确保适应度比平均适应度大的一些个体能够被遗传到下一代群体中，因而选择误差比较小。

7. 均匀排序：对群体中的所有个体按期适应度大小进行排序，基于这个排序来分配各个个体被选中的概率。

8. 最佳保存策略：当前群体中适应度最高的个体不参与交叉运算和变异运算，而是用它来代替掉本代群体中经过交叉、变异等操作后所产生的适应度最低的个体。

9. 随机联赛选择：每次选取几个个体中适应度最高的一个个体遗传到下一代群体中。

10. 排挤选择：新生成的子代将代替或排挤相似的旧父代个体，提高群体的多样性。

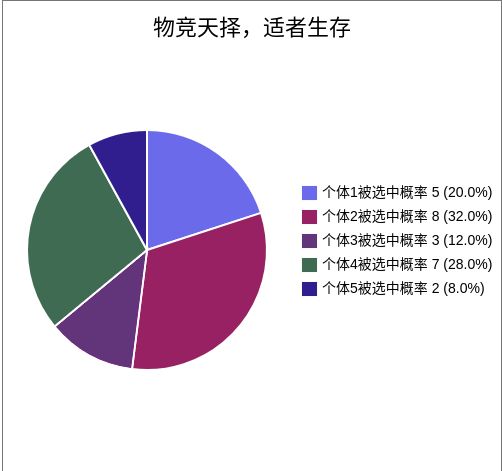
下面以轮盘赌选择为例给大家讲解一下：

假如有５条染色体，他们的适应度分别为５、８、３、７、２。

那么总的适应度为：F = 5 + 8 + 3 + 7 + 2 = 25。

那么各个个体的被选中的概率为：

α1 = ( 5 / 25 ) * 100% = 20%

α2 = ( 8 / 25 ) * 100% = 32%

α3 = ( 3 / 25 ) * 100% = 12%

α4 = ( 7 / 25 ) * 100% = 28%

α5 = ( 2 / 25 ) * 100% = 8%

 

可以看出，适应性越高的个体被选中的概率就越大。

• 其次是交叉(crossover)
  • 两个待交叉的不同的染色体(父母)根据交叉概率(cross_rate)按某种方式交换其部分基因
  • 采用单点交叉法，也可以使用其他交叉方法

适用于二进制编码个体或浮点数编码个体的交叉算子：

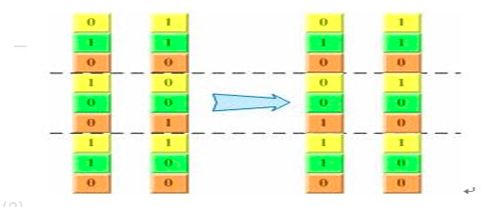
1. 单点交叉（One-point Crossover）：指在个体编码串中只随机设置一个交叉点，然后再该点相互交换两个配对个体的部分染色体。

2. 两点交叉与多点交叉：

   (1) 两点交叉（Two-point Crossover）：在个体编码串中随机设置了两个交叉点，然后再进行部分基因交换。

   (2) 多点交叉（Multi-point Crossover）

3. 均匀交叉（也称一致交叉，Uniform Crossover）：两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换，从而形成两个新个体。

4. 算术交叉（Arithmetic Crossover）：由两个个体的线性组合而产生出两个新的个体。该操作对象一般是由浮点数编码表示的个体。

对应的二进制交叉：

• 最后是变异(mutation)
  • 染色体按照变异概率(mutate_rate)进行染色体的变异
  • 采用单点变异法，也可以使用其他变异方法

例如下面这串二进制编码：

101101001011001

经过基因突变后，可能变成以下这串新的编码：

001101011011001

以下变异算子适用于二进制编码和浮点数编码的个体：

• 基本位变异（Simple Mutation）：对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。

• 均匀变异（Uniform Mutation）：分别用符合某一范围内均匀分布的随机数，以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。（特别适用于在算法的初级运行阶段）

• 边界变异（Boundary Mutation）：随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。

• 非均匀变异：对原有的基因值做一随机扰动，以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后，相当于整个解向量在解空间中作了一次轻微的变动。

• 高斯近似变异：进行变异操作时用符号均值为Ｐ的平均值，方差为P**2的正态分布的一个随机数来替换原有的基因值。

 

 

---

这篇重点介绍原理，下篇将介绍运用Python完成实例操作。

参阅：

百度百科：遗传算法

【算法】超详细的遗传算法(Genetic Algorithm)解析

遗传算法详解（GA）

详解遗传算法

知乎

https://www.zhihu.com/question/23293449/answer/120220974