“华为杯”大连理工大学第15届大学生程序设计大赛（验题人题解）

M：A+B

临时加的签签到到题

L：数学

代进去求一下，签到题

#include
using namespace std;
typedef long long ll;
typedef pair P;
int v;
int main(){
	puts("217341");
	return 0;
} 

H：书

签到题，

注意到如果是全相同的字母的串，比如aaaaa，只能全删

否则出现了两种字母，如abba，abcba，ddz

如果不是回文串，显然不用删；

否则，把最后一个字母删掉即可

#include
using namespace std;
typedef long long ll;
typedef pair P;
int T;
char s[205];
int cal(){
	bool sm=1;
	int n=strlen(s);
	for(int i=1;i

A： Lucky Number その１

签到题，对区间内每个数暴力统计即可

#include
using namespace std;
typedef long long ll;
typedef pair P;
const int N=5e5+10;
int t,n,k,x,y;
int cal(int x){
	int c=0;
	for(;x;x/=10){
		if(x%10==4)c++;
		else{
			if(c==1 || c==2)return 0;
			c=0;
		}
	}
	if(c==1 || c==2)return 0;
	return 1; 
}
int main(){
	while(~scanf("%d%d",&x,&y)){
		if(x==-1 && y==-1)break;
		t++;
		assert(0<=x && x<=y && y<=100000);
		int ans=0;
		for(int i=x;i<=y;++i){
			ans+=cal(i);
		}
		printf("%d\n",ans);
	}
	assert(t<=6);
	return 0;
} 

E： 完美数组

分类讨论，贪心，遵循两条原则，

1.前面尽量正负交替，开头的值用多的那个

2.在前面能不用零尽量不用零，零可以放在任意位置，还能block两个同符号的值

#include
using namespace std;
const int N=1e3+10;
int t,n,v,zero,ans[N];
vectorz,f;
bool solve(){
	int c=0;
	for(int i=1;i<=n;++i){
		if(c>=1){
			if(ans[c]>0){
				if(f.size()){
					int v=f.back();f.pop_back();
					ans[++c]=v;
				}
				else if(zero){
					zero--;
					ans[++c]=0;
				}
				else{
					return 0;
				}
			}
			else if(ans[c]<0){
				if(z.size()){
					int v=z.back();z.pop_back();
					ans[++c]=v;
				}
				else if(zero){
					zero--;
					ans[++c]=0;
				}
				else{
					return 0;
				}
			}
			else{
				if(!z.size() && !f.size()){
					zero--;
					ans[++c]=0;
				}
				else if(z.size()>f.size()){
					int v=z.back();z.pop_back();
					ans[++c]=v; 
				}
				else{
					int v=f.back();f.pop_back();
					ans[++c]=v;
				}
			}
		}
		else{
			if(!z.size() && !f.size()){
				zero--;
				ans[++c]=0;
			}
			else if(z.size()>f.size()){
				int v=z.back();z.pop_back();
				ans[++c]=v; 
			}
			else{
				int v=f.back();f.pop_back();
				ans[++c]=v;
			}
		}
	}
	return 1;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		zero=0;z.clear();f.clear();
		for(int i=1;i<=n;++i){
			scanf("%d",&v);
			if(v==0)zero++;
			else if(v<0)f.push_back(v);
			else z.push_back(v);
		}
		if(!solve())puts("NO");
		else{
			puts("YES");
			for(int i=1;i<=n;++i){
				printf("%d ",ans[i]);
			}
			puts("");
		}
	}
	return 0;
} 

G：积木

我：第一签到题

夏老师：真的吗真的吗真的吗

预期的签到题，但好像不太符合预期

可能是因为大家不一定打过icpc昆明/徐州

 

注意到一个事实，如果[1,i]的和大于等于i+1，则它们也能凑出[1,i+1]的和

所以，k<=2的时候答案为k，否则能不断吞并，为sum-k+1

#include
using namespace std;
typedef long long ll;
typedef pair P;
int T,n,k;
int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%d%d",&n,&k);
		if(k<=2)printf("%d\n",k);
		else printf("%lld\n",1ll*n*(n+1)/2-k+1);
	}
	return 0;
} 

C: 高空走钢索

在只有一个人或两个人的时候，一趟即可，

考虑四个人的情形，在有1 2 3 4四个人（认为1时间最短4时间最长）的时候，

要么是12先过去，1回，34再过去，2回，然后只剩12，

要么是14先过去，1回，13再过去，1回，然后只剩12

i个人规模递归到i-2个人规模，所以做个dp即可

#include
using namespace std;
typedef long long ll;
const int N=1e3+10;
int t,n,a[N];
ll dp[N];
int main(){
	scanf("%d",&t);
	assert(t<=100);
	while(t--){
		scanf("%d",&n);
		assert(n<=1000);
		for(int i=1;i<=n;++i){
			scanf("%d",&a[i]);
			assert(a[i]<=100000);
		}
		sort(a+1,a+n+1);
		dp[1]=a[1];dp[2]=a[2];
		for(int i=3;i<=n;++i){
			dp[i]=min(dp[i-1]+a[i]+a[1],dp[i-2]+a[2]+a[1]+a[i]+a[2]);
		}
		printf("%lld\n",dp[n]);
		//assert(dp[n]<=1ll<<32);
	}
	return 0;
} 

B: Lucky Number その２

注意到范围1e18，所以只能数位dp

可能大家的做法都不太一样，验题人的做法是，

直接做不太好做，所以考虑用总的减掉不合法的方案数，

所以，需要统计出现了长度为1的4或长度为2的4的方案，

dp[i][j][0/1]表示当前在第i位连续遇到了j个4是否已经出现了一段长度为1的4或者一段长度为2的4的方案数

然后数位dp套套模板，枚举下这位填几，会不会给连续的4产生影响，有没有出现一段长为1的4或者长为2的4

真的猛士，敢于先写B后写A

#include
using namespace std;
typedef long long ll;
typedef pair P;
const int N=5e5+10;
ll x,y,a[20],dp[20][20][2];
ll dfs(int x,int four,bool has,bool up){
	//printf("x:%d four:%d has:%1d up:%1d\n",x,four,has,up);
	if(x==0){
		return has==1 || four==1 || four==2;
	}
	if(!up && ~dp[x][four][has]){
		return dp[x][four][has];
	}
	ll ans=0;
	int lim=up?a[x]:9;
	for(int i=0;i<=lim;++i){
		if(four==1 || four==2){
			if(i==4){
				ans+=dfs(x-1,four+1,has,up && i==lim);
			}
			else{
				ans+=dfs(x-1,0,1,up && i==lim);
			}
		}
		else{
			if(i==4){
				ans+=dfs(x-1,four+1,has,up && i==lim);
			}
			else{
				ans+=dfs(x-1,0,has,up && i==lim);
			}
		}
	}
	if(!up)dp[x][four][has]=ans;
	//printf("x:%lld four:%lld has:%lld dp:%lld\n",x,four,has,dp[x][four][has]);
	return ans;
}
ll cal(ll x){
	if(x<=0)return 0;
	int c=0;
	for(;x;x/=10){
		a[++c]=x%10;
	}
	memset(dp,-1,sizeof dp);
	return dfs(c,0,0,1);
}
int main(){
	while(~scanf("%lld%lld",&x,&y)){
		if(x==-1 && y==-1)break;
		ll n=y-x+1,ill=cal(y)-cal(x-1);
		//printf("n:%lld ill:%lld",n,ill);
		printf("%lld\n",n-ill);
	}
	return 0;
} 

J：猫

出题人：你看看这个题

我：你这不是原题，hdu6187

出题人：不是啊，是日本icpc2010的题

于是出题人没有改悔，可能下次还会再犯

 

考虑拆掉的最小，于是保留的最大，

保留的部分是没有环的，所以是求个最大生成树

#include
using namespace std;
typedef long long ll;
typedef pair P;
const int N=1e4+10,M=3e4+10;
int n,m;
int par[N];
P a[N];
double sum,ans;
int find(int x){
	return par[x]==x?x:par[x]=find(par[x]);
}
struct node{
	int u,v;
	double w;
}e[M];
bool operator<(node a,node b){
	return a.w>b.w; 
};
double sq(double x){
	return x*x; 
}
double cal(P a,P b){
	return sqrt(sq(a.first-b.first)+sq(a.second-b.second));
}
int main(){
	scanf("%d%d",&n,&m);
	//if(n==10000)while(1); 
	assert(1<=n && n<=10000);
	assert(1<=m && m<=30000);
	for(int i=1;i<=n;++i){
		par[i]=i;
		scanf("%d%d",&a[i].first,&a[i].second);
		assert(-10000<=a[i].first && a[i].first<=10000);
		assert(-10000<=a[i].second && a[i].second<=10000);
	}	
	for(int i=1;i<=m;++i){
		scanf("%d%d",&e[i].u,&e[i].v);
		assert(1<=e[i].u && e[i].u<=n);
		assert(1<=e[i].v && e[i].v<=n);
		assert(e[i].u!=e[i].v);
		e[i].w=cal(a[e[i].u],a[e[i].v]);
	}
	sort(e+1,e+m+1);
	for(int i=1;i<=m;++i){
		int u=find(e[i].u),v=find(e[i].v);
		sum+=e[i].w;
		if(u==v)continue;
		par[v]=u;ans+=e[i].w;
	}
	printf("%.10lf\n",sum-ans);
	return 0;
} 

K：画

先假设所有都自己完成，然后考虑哪些能翻转，

考虑第i天抄了第j次，则(i-1)-(j-1)次自己完成，最后获得(2*(j-1)-(i-1)+P)*Q的收益，

相比自己完成，额外收益是(2*(j-1)-(i-1)+P)*Q-c[i]=2*(j-1)*Q+P*Q-(i-1)*Q-c[i]

注意到i、j分离之后，可以分别统计贡献，

考虑枚举一共抄了j次，则2*(j-1)*Q的和固定，

只需求前j大的-(i-1)*Q-c[i]，这个排序一下即可

 

被出题人教育了，才得出来的做法，

我一开始的做法是先都抄，然后倒着dp[i]维护后缀抄了i天的最大收益

抄作业不快乐么

#include
using namespace std;
typedef long long ll;
typedef pair P;
const int N=5e5+10;
int n,p,q,c[N],id[N];
ll ans,tmp;
bool cmp(int x,int y){	
	return 1ll*(x-1)*p+c[x]<1ll*(y-1)*p+c[y];
}
int main(){
	scanf("%d%d%d",&n,&p,&q);
	assert(1<=n && n<=500000);
	assert(0<=p && p<=500000);
	assert(abs(q)<=500000);
	for(int i=1;i<=n;++i){
		scanf("%d",&c[i]);
		assert(abs(c[i])<=500000);
		tmp+=c[i];
		id[i]=i;
	}
	sort(id+1,id+n+1,cmp);
	ans=tmp;
	for(int j=1;j<=n;++j){
		tmp-=1ll*(id[j]-1)*p+c[id[j]];
		tmp+=2ll*(j-1)*p+1ll*p*q;
		ans=max(ans,tmp);
	}
	printf("%lld\n",ans);
	return 0;
} 

F: 完美数对

据说是微信的面试题，巧妙构造，

但是我不会，充分体现了没有脑子，

赛后：好耶，大家也没有脑子

 

首先注意到k>C(n,2)一定没解，否则一定有解，

如果，我们能找到2*i是完全平方数，2*j是完全平方数，i+j是完全平方数

则总共放了x个i、j，x个点内部是一个团（两两有边），贡献是x*(x-1)/2

这里采取打表的方式，找到了一组(i,j)=(2,98)，

 

找到满足x*(x-1)/2<=k的最大x，然后还剩k-x*(x-1)/2条边

如果k-x*(x-1)/2=0，就随便放不会影响答案的值即可，

否则，钦定一个和2能连边的值，由此确定了2的个数

此时，如果还有多余的，随便放不会影响答案的值即可

#include
using namespace std;
typedef long long ll;
typedef pair P;
const int N=5e5+10;
int t,n,k,x,y;
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&k);
		if(k>n*(n-1)/2){
			puts("No");
			continue;
		} 
		puts("Yes");
		for(x=0;x*(x-1)/2<=k;++x);x--;
		y=k-x*(x-1)/2;
		if(!y){
			for(int i=1;i<=x;++i){
				printf("%d ",2);
			}	
			for(int i=1;i<=n-x;++i){
				printf("%d ",3);
			}
		}
		else{
			for(int i=1;i<=y;++i)printf("%d ",2);
			for(int i=1;i<=x-y;++i)printf("%d ",98);
			printf("%d ",223);
			for(int i=1;i<=n-x-1;++i)printf("%d ",1);
		}
		puts("");
	}
	return 0;
} 

D: 正方形数数

验题人是O(n^2logn)乱搞过的，我永远喜欢数据结构.jpg

官方题解有O(n^2)的做法，我不听我不听我不听

 

样例给了启发，

首先l、r、u、d分别维护左右上下相同的能扩展的长度，

然后考虑怎么统计答案，这里是枚举对角线从左上到右下，

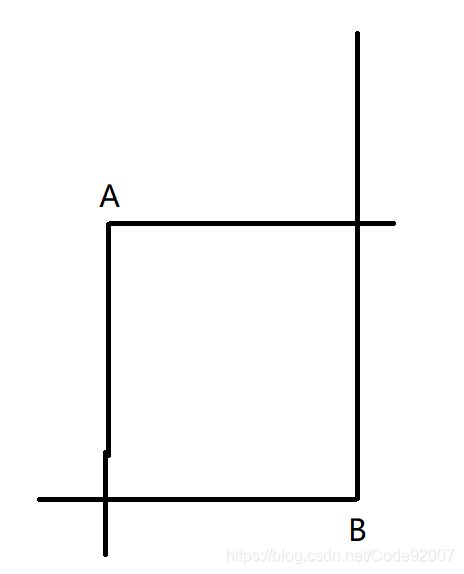
考虑B点维护一个向左向上的壳，A点插入一个向右向下的壳，

如果A能覆盖到B且B能覆盖到A，且AB值相同就是一个合法的正方形，

所以考虑每条对角线的平行线，开一个树状数组

同一条线上的所有排序，第一关键字是值，第二关键字是位置，

 

对所有相同的值尺取，先插入再统计答案，然后撤销掉

记A的位置是同一条线上的pos，向右下cover的范围是[pos,pos+v-1]（线段1）

其中，v是向右向下二者的短边的长度，

则B的位置是pos2，向左上cover的范围是[pos2-w+1,pos2]（线段2）

其中，w是向左向上二者的短边的长度，

A、B构成一个合法的正方形当且仅当线段1覆盖住pos2且线段2覆盖住pos1

 

这是一个经典问题，这里的做法是，

先把A在pos点插入，在pos+v点撤销（这里用了一个优先队列）

然后B经过的时候，统计区间内值的方案数即可

#include
using namespace std;
typedef pair P;
const int N=1e3+10,M=2e3+5,off=1e3;
int tr[M][N],l[N][N],r[N][N],u[N][N],d[N][N];
int n,m,a[N][N],ans;
priority_queue,greater
 >q;
void add(int id,int x,int v){
	for(int i=x;i0;i-=i&-i){
		ans+=tr[id][i];
	}
	return ans;
}
struct node{
	int id,x,y,v;
}e[N];
bool cmp(node a,node b){
	return a.v=1;--i){
		for(int j=m;j>=1;--j){
			r[i][j]=(a[i][j]==a[i][j+1]?r[i][j+1]+1:1);
			d[i][j]=(a[i][j]==a[i+1][j]?d[i+1][j]+1:1);
		}
	}
	for(int dig=1-n;dig<=m-1;++dig){
		int i,j,c=0,id=dig+off;
		if(dig<=0)j=1,i=j-dig;
		else i=1,j=i+dig;
		for(;i<=n&&j<=m;++i,++j){
			++c;
			e[c]={c,i,j,a[i][j]};
		}
		sort(e+1,e+c+1,cmp);
		for(int x=1;x<=c;){
			int y=x;
			while(y+1<=c && e[y+1].v==e[x].v){
				y++;
			}
			for(int z=x;z<=y;++z){
				i=e[z].x,j=e[z].y;
				int pos=min(i,j);
				int w=min(l[i][j],u[i][j]);
				int v=min(r[i][j],d[i][j]);
				while(!q.empty() && q.top().first<=pos){
					int r=q.top().second;q.pop();
					add(id,r,-1);
				}
				add(id,pos,1);
				//printf("a:%d b:%d\n",sum(id,pos),sum(id,pos-w));
				q.push(P(pos+v,pos));
				int more=sum(id,pos)-sum(id,pos-w); 
				//printf("w:%d\n",w);
				ans+=more;
				//printf("i:%d j:%d more:%d\n",i,j,more);
			}
			while(!q.empty()){
				int r=q.top().second;q.pop();
				add(id,r,-1);
			}
			x=y+1;
		}
	}
	printf("%d\n",ans);
	return 0;
}

I: 棋

验题人不会，给的定位是防AK题，可以参考官方题解

大概思路是，先把曼哈顿距离转成切比雪夫距离

然后考虑维护一个四维dp，

dp[i][j][k][l]控制xmin,xmax,ymin,ymax，

每次加入一行或一列统计贡献

 

验题人的贡献及吐槽

修复了完美数组spj的bug，

修复了完美数组的样例数，书的字符长度的bug

乱搞了若干暴力做法、假做法没有艹过去，

构造造了个越界的也没有艹过去，

好家伙，全都防住了啊，那就是没锅了

 

个人认为，出题人出了一套好题，没有模板题，好评好评~

 

主校区与软院负责参与策划、布置、监考、出题、验题的同学们都辛苦了~

参赛的同学们也辛苦了~