2020年第十一届蓝桥杯第二场省赛B组C++题解

题单

第一题

小蓝要为一条街的住户制作门牌号。
这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。
小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、0、1、7，即需要 1 个字符 0，2 个字符 1，1 个字符 7。
请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？
答案：624
代码描述：

#include
using namespace std;
int ans; 
int isok(int n)
{
     
	int sum=0;
	while(n){
     
		int t=n%10;
		if(t==2) sum++;
		n/=10;
	}
	return sum;
}
int main()
{
     
	for(int i=1;i<=2020;i++){
     
		ans+=(isok(i));
	}
	cout<<ans;
	return 0;
}

第二题

如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。
例如，3/4 , 5/2 , 1/8 , 7/1 都是既约分数。
请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？

答案：2481215
代码描述

#include
using namespace std;
int ans;

int gcd(int a,int b)
{
     
	return b==0?a:gcd(b,a%b);	
}

int main()
{
     
	for(int i=1;i<=2020;i++){
     
		for(int j=1;j<=2020;j++){
     
			if(gcd(i,j)==1) ans++;
		}
	}
	cout<<ans;
	return 0;
}

第三题

下图所示，小明用从 1 开始的正整数“蛇形”填充无限大的矩阵。
1 2 6 7 15 …
3 5 8 14 …
4 9 13 …
10 12 …
11 …
…
容易看出矩阵第二行第二列中的数是 5。请你计算矩阵中第 20 行第 20 列的数是多少？
答案：761
代码描述

#include
using namespace std;
int next[4][2]={
     {
     0,1},{
     1,-1},{
     1,0},{
     -1,1}};
int a[55][55];
int main()
{
     
	int x=1,y=1,ans=1,t=0,k=-1;
	while(x!=40||y!=40){
         //第二十行二十列可能需要到40行40列左右相加 
		a[x][y]=ans++;
		x+=next[t][0];
		y+=next[t][1];
		if(t==0||t==2)  k++;
		if(x<1||x>40||y<1||y>40||a[x][y]!=0||k==1){
     
			if(k==1) k=0;
			x-=next[t][0];
			y-=next[t][1];
			t=(t+1)%4;
			x+=next[t][0];
			y+=next[t][1];
		}
	}
	/*
	for(int i=1;i<=40;i++){
		for(int j=1;j<=40;j++){
			cout<
	cout<<a[20][20];
	return 0;
}

第四题

小蓝每天都锻炼身体。
正常情况下，小蓝每天跑 1 千米。如果某天是周一或者月初（1 日），为了激励自己，小蓝要跑 2 千米。如果同时是周一或月初，小蓝也是跑 2 千米。
小蓝跑步已经坚持了很长时间，从 2000 年 1 月 1 日周六（含）到 2020 年10 月 1 日周四（含）。请问这段时间小蓝总共跑步多少千米？
答案：8879
题解思路：Excel大法好啊！！！
首先算出两者相隔的天数是7579天，因题目说第一天就开始跑了，所有加上1，总共跑的天数就是7580天，每天1公里，也就是7580公里了。

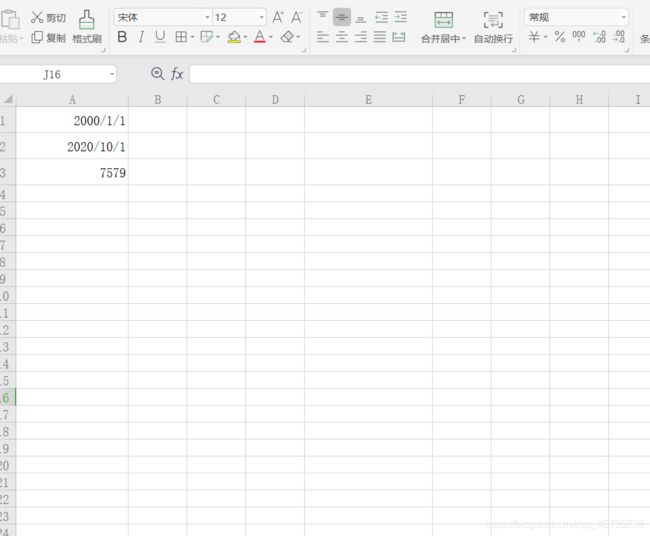
接着算上这7580天里共有几个周一，通过代码我们知道共有1083个周一，所以每周一再多跑1公里，总共就跑了7580+1083=8663公里。

#include
using namespace std;
int main()
{
     
	int ans=0;
	for(int i=3;i<=7580;i+=7){
       //当i=1时，此时为周六，咱们从i=3，
	                           //即下周一开始算起
		ans++;
	}
	cout<<ans;
	return 0;
}

然后在算上从2000/1/1到2020/10/1共有多少个月初。从数据上看我们知道一共有20年+10个月，所以总月份数位20*12+10=250个月（我塔喵算成20*24+10，绝望），也就是这250个月初里还要多跑250公里。所以总公里数为：8663+250=8913。
最后，如果月初和周一重合咱们也是只跑两公里的，通过日历（别问，问就是一个个数的）我们知道共有34个重合数，所以总公里数为：8913-34==8879

第五题

最后没时间了随便填了个28。。。考虑到DFS+连通块，但是不会建图。

第六题

小蓝给学生们组织了一场考试，卷面总分为100分，每个学生的得分都是一个0到100的整数。
如果得分至少是60分，则称为及格。如果得分至少为85分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整
数。

round(double x) 该函数用于将double型变量x四舍五入，返回类型也是double ，注意只能对小数点后一位进行 四舍五入

#include
using namespace std;
int yx , jg;
int main()
{
     
	//round(double x) 该函数用于将double型变量x四舍五入，返回类型也是double ，注意
	//只能对小数点后一位进行 四舍五入
	
	int n , x;
	cin >> n;
	for(int i = 1 ; i <= n ; i ++){
     
		cin >> x;
		if(x >=85) yx ++;
		if(x >=60) jg ++;
	}
	printf("%d%\n%d%\n" , (int)round(jg * 100.0 / n) , (int)round(yx * 100.0 / n));
	
//	printf("%f %d %f %d" , round(3.5) , (int)round(3.45) , round(3.45 * 10) / 10 , (int)round(3.445 * 100));
	return 0;
}

第七题

2020 年春节期间，有一个特殊的日期引起了大家的注意：2020 年 2 月 2日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202，恰好是一个回文数。我们称这样的日期是回文日期。有人表示 20200202 是 “千年一遇” 的特殊日子。
对此小明很不认同，因为不到 2 年之后就是下一个回文日期：20211202 即 2021 年 12 月 2 日。也有人表示 20200202 并不仅仅是一个回文日期，还是一个 ABABBABA型的回文日期。对此小明也不认同，因为大约 100 年后就能遇到下一个ABABBABA 型的回文日期：21211212 即 2121 年 12 月 12 日。算不上 “千年一遇”，顶多算 “千年两遇”。
给定一个 8 位数的日期，请你计算该日期之后下一个回文日期和下一个ABABBABA 型的回文日期各是哪一天。

答：没有判断日期合法性，我、又没了。。
赛后很快就写出了正确答案：

#include
using namespace std;
typedef long long ll;
int y , m , d , f1 , f2 , ans1 , ans2;
int Month[13][2] = {
     {
     0,0},{
     31,31},{
     30,30},{
     31,31},{
     30,30},{
     31,31},{
     30,30},{
     31,31},{
     31,31},{
     30,30},{
     31,31},{
     30,30},{
     31,31}};
int isrun(int year)
{
     
	return year % 400 == 0 || year % 4 == 0 && year % 100 != 0;
}

int judge1(int sum)
{
     
	int a[20] , k = sum , cnt = 1;
	do{
     
		a[cnt ++] = sum % 10;
		sum /= 10;
	}while(sum);
	for(int i = 1 , j = cnt - 1 ; i < j ; i ++ , j --){
     
		if(a[i] != a[j]) return 0;
	}
	return 1;
}

int judge2(int sum)
{
     
	int a[20] , k = sum , cnt = 1;
	do{
     
		a[cnt ++] = sum % 10;
		sum /= 10;
	}while(sum);
	if(a[1] != a[3] || a[1] != a[6] || a[1] != a[8] || a[3] != a[6] || a[3] != a[8] || a[6] != a[8] ||
		a[2] != a[4] || a[2] != a[5] || a[2] != a[7] || a[4] != a[5] || a[4] != a[7] || a[5] != a[7] ||
		a[1] == a[2] || a[1] == a[4] || a[1] == a[5] || a[1] == a[7])
		return 0;
		return 1;
}
int main()
{
     
	int n ;
	cin >> n;
	y = n / 10000;
	m = n % 10000 / 100;
	d = n % 100;
	while(1){
     
		d ++;
		if(d > Month[m][isrun(y)]){
     
			d = 1;
			m ++;
			continue;
		}
		if(m > 13){
     
			m = 1;
			y ++;
			continue;
		}
		int ans = y * 10000 + m * 100 + d;
		if( f1 == 0 && judge1(ans) ){
     
			ans1 = ans;
			f1 = 1;	
		}
		if(f2 == 0 && judge2(ans)){
     
			ans2 = ans;
			f2 = 1;
		}
		if(f1 && f2) break;
	}
	printf("%04d%02d%02d\n" , ans1 / 10000 , ans1 % 10000 / 100 , ans1 % 100);
	printf("%04d%02d%02d" , ans2 / 10000 , ans2 % 10000 / 100 , ans2 % 100);
}

第八题

于一个字符串 S，我们定义 S 的分值 f (S ) 为 S 中出现的不同的字符个数。例如 f (”aba”) = 2， f (”abc”) = 3, f (”aaa”) = 1。
现在给定一个字符串 S [0::n ? 1]（长度为 n），请你计算对于所有 S 的非空子串 S [i:: j](0 ≤ i ≤ j < n)， f (S [i:: j]) 的和是多少
答：只会暴力
代码描述

#include
using namespace std;
string s;
int book[100] , sum;
int main()
{
     
	cin >> s;
	int len = s.size();
	for(int i = 0 ; i < len ; i ++){
     
		int cnt = 0;
		for(int j = i ; j < len ; j ++){
     
			int word = s[j] - 'a';
			if(book[word] == 0){
     
				book[word] = 1;
				cnt ++;
			}
			sum += cnt;
		}
		fill(book , book + 100 , 0);
	}
	cout << sum;
	return 0;
}