Github项目地址
https://github.com/JackManTvO/sudoku
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 12 |
| Estimate | 估计这个任务需要多少时间 | 20 | 12 |
| Development | 开发 | 520 | 890 |
| Analysis | 需求分析(包括学习新技术) | 120 | 170 |
| Design Spec | 生成设计文档 | 30 | 55 |
| Design Review | 设计复审(和同时审核设计文档) | 20 | 15 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 20 | 10 |
| Design | 具体设计 | 60 | 80 |
| Coding | 具体编码 | 180 | 400 |
| Code Review | 代码复审 | 30 | 40 |
| Test | 测试(自我测试,修改代码,提交修改) | 60 | 120 |
| Reporting | 报告 | 100 | 63 |
| Test Report | 测试报告 | 60 | 40 |
| Size Measurement | 计算工作量 | 10 | 10 |
| Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 30 | 13 |
| 合计 | 640 | 965 |
解题思路
生成数独终局
数独的要求是在9×9的格子内,每一行和每一列和每一宫内都包含不重复的九个元素,但数独终局的个数共有6,670,903,752,021,072,936,960(6.67×10²¹)种组合,尽管终局要求左上角第一个数字为固定值,其终局的种数也是巨大的。而程序设计对终局数量的需求仅在1,000,000个以内,因此,没有必要穷举找到前1,000,000种终局,而没有合适的生成策略随机生成则可能造成终局的重复。因此需制定合适的生成终局策略,而我的生成终局策略为对固定的终局模板进行数字交换以及行交换。这种策略共可以生成8!(除首数字外8个数字两两交换)×2(23行交换)×6(4~6行两两交换)×6(7~9行两两交换)=2,903,040种终局,大于要求的终局数。根据要求生成的终局个数对变换方式进行深度优先搜索,第一层为数字交换,第二层为23行交换,第三层为4~6行交换,第四层为7~9行交换,以快速地遍历第四层的叶子,以生成多个不重复的终局。
具体步骤如下:
- 生成一固定的有效终局作为模板。
- 对模板进行数字交换。
- 对进行数字交换后的终局进行行交换(2~3行交换、4~6行交换、7~9行交换)保证宫内不重复。
- 若生成终局数满足程序要求个数即返回,若不满足,重复进行步骤2、步骤3。
求解数独谜题
对于给定的数独谜题,按要求补充数独的空缺,以完成数独。因为填入的数需要满足数独的要求,所以每个固定位置的数值是有限制的,在剩余的可行值中选择一个填入空白,接着填入下一个空白。若发现无可行解,则父节点选择错误,采用回溯法,返回上一节点,填入另一可行解。直到生成树的层数等于空缺数,则生成一可行的数独终局,求解数独谜题成功。
具体步骤如下:
- 扫描题目,将空白值坐标取出存入数组A。
- 在数组A中选择下一个坐标。
- 查询其所在行、列、宫的数值,填入可行解数组,在可行解数组中选取下一可行解填入。
- 若填入成功,则返回步骤2,若无可行解,则在数组A中返回上一坐标,返回步骤3填入另一可行解。若A中无剩余,则返回,求解数独成功。
设计实现过程
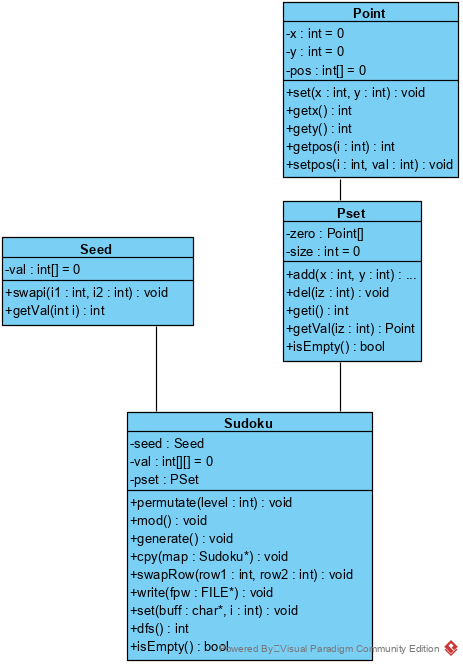
类
我设计了三个类,分别为向量类、点类和数独类(改进前)
Seed类(改进前)
| 变量名称 | 类型 | 说明 |
|---|---|---|
| val | int[9] | 生成向量值 |
| 接口名称 | 参数类型 | 返回类型 | 功能 |
|---|---|---|---|
| Seed | null | null | 根据宏定义的首数字生成生成向量 |
| swapi | int(脚标1),int(脚标2) | null | 根据脚标交换向量中两数的位置 |
| getVal | int(脚标) | int(结果) | 根据脚标查询向量中数值 |
Point类(改进前)
| 变量名称 | 类型 | 说明 |
|---|---|---|
| x | int | 横坐标 |
| y | int | 纵坐标 |
| pos | int[10] | 点的可行解标识 |
| 接口名称 | 参数类型 | 返回类型 | 功能 |
|---|---|---|---|
| Point | null | null | 初始化类 |
| Point | Point*(实例) | null | 初始化类使其值与实例相同 |
Sudoku类(改进前)
| 变量名称 | 类型 | 功能 |
|---|---|---|
| seed | Seed | 生成向量 |
| val | int[9][9] | 数独 |
| zero | Point[60] | 空缺点集合 |
| 接口名称 | 参数类型 | 返回类型 | 功能 |
|---|---|---|---|
| permuate | int(层数) | null | 根据层数dfs全排列 |
| mod | null | null | 根据生成向量生成模板 |
| generate | null | null | 全排列交换行生成终局 |
| cpy | const Sudoku*(模板) | null | 根据模板复制数独 |
| swapRow | int(行数1),int(行数2) | null | 交换两行数值 |
| write | FILE*(文件) | null | 将数独写入文件 |
| set | char*(字符串),int(行数) | null | 将文件读出,按行给数独赋值 |
| dfs | null | int(记号) | 深度优先搜索,成功返回1,失败返回0 |
类图(改进后)
关键函数
元素交换函数
行交换函数
解数独函数
单元测试设计
使用了代码走读,并对三个关键函数使用路径测试法进行了单元测试:
元素交换函数
| 路径 | 输入数据 | 输出数据 |
|---|---|---|
| path1 | level=7 | 多个模板和终局 |
| path2 | level=10 | 无预期输出 |
| path3 | level=6,nsudoku=0 | 无预期输出 |
| path4 | level=6,nsudoku=1 | 1个终局 |
行交换函数
| 路径 | 输入数据 | 输出数据 |
|---|---|---|
| path1 | nsudoku=72 | 72个模板和终局 |
解数独函数
| 路径 | 输入数据 | 输出数据 |
|---|---|---|
| path1 | 空点集 | 无预期输出 |
| path2 | 包含3个点的点集 | 3个点值确定 |
改进
终局生成
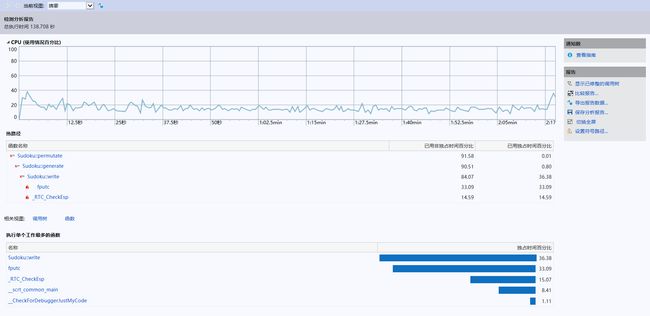
设置参数需要的棋盘数量为1,000,000,对该改进前代码进行了10次性能分析,平均时间为138.251秒,最接近平均时间的一次为138.708秒。
由性能分析可见,消耗最大的函数是Sudoku类的写文件函数中的fputc函数,为了方便添加空格,我采用的是fputc函数逐个添加字符,且运行write函数后就关闭文件。这样在1,000,000个终局生成中,会发生反复调用fputc函数和打开、关闭文件函数。因此我改动为在开始生成终局时打开文件,在写入完成后关闭文件,将字符连接为字符串后,将一整个数独终局以字符串写入文件。且Point类的封装性不强,我加强了Point类的封装性(见类图)。改进前在行交换时,回溯时需要置为交换前,浪费大量时间,我在行变换前,将数独终局作为新变量保存以作为模板,方便进行二次行交换。
改进后10次性能分析的平均时间为5.137秒,最接近平均时间的一次为5.368秒。
由性能分析可见,改进后代码平均时间减少为改进前的3.716%,大大缩短了生成时间。
数独求解
为了方便进行数独求解,我添加了Pset类已保存空白点(见类图),且封装性良好。为了优化性能,我采用了随机的策略选取下一空白点的解,并记录空白点处理的顺序以方便回溯。这个算法的时间复杂度明显优于全图遍历。且为了减少数据的冗余,在读入数独时完成空白点集的添加。
代码说明
元素交换函数
void Sudoku::permutate (int level) {
if (level == side - 2) { //全排列结束
mod (); //生成模板
generate (); //行交换
return;
}
for (int i = level; i < side; i++) {
if (i != level)
seed.swapi (level, i); //交换元素
permutate (level + 1); //递归
if (nsudoku == 0)
return;
if (i != level)
seed.swapi (level, i);
}
return;
}
行交换函数
void Sudoku::generate () { //生成终局
/*行变换*/
Sudoku ans;
for (int i = 0; i < 2 && nsudoku>0; i++) //第一阶段
for (int j = 0; j < 6 && nsudoku>0; j++) //第二阶段
for (int k = 0; k < 6 && nsudoku>0; k++) { //第三阶段
ans.cpy(this);
switch (i) {
case 0:
break;
case 1:
ans.swapRow (1, 2); break;
}
switch (j) {
case 0:
break;
case 1:
ans.swapRow (4, 5); break;
case 2:
ans.swapRow (3, 4); break;
case 3:
ans.swapRow (3, 5); ans.swapRow (3, 4); break;
case 4:
ans.swapRow (3, 4); ans.swapRow (3, 5); break;
case 5:
ans.swapRow (3, 5); break;
}
switch (k) {
case 0:
break;
case 1:
ans.swapRow (7, 8); break;
case 2:
ans.swapRow (6, 7); break;
case 3:
ans.swapRow (6, 8); ans.swapRow (6, 7); break;
case 4:
ans.swapRow (6, 7); ans.swapRow (6, 8); break;
case 5:
ans.swapRow (6, 8); break;
}
ans.write (fpw);
nsudoku--; //生成数+1
if (nsudoku == 0) {
if (fpw != NULL)
fclose (fpw);
return;
}
if (fpw != NULL)
fprintf (fpw, "\n\n");
}
return;
}
解数独函数
int Sudoku::dfs () {
int iz = pset.geti();
Point p (this->pset.getVal(iz));
/*初始化占有标识数组*/
for (int i = 0; i < 9; i++) {
if (val[p.getx ()][i] != 0 && p.getpos (val[p.getx ()][i]) == 0)
p.setpos (val[p.getx ()][i], 1);
if (val[i][p.gety ()] != 0 && p.getpos (val[p.getx ()][i]) == 0)
p.setpos (val[i][p.gety ()], 1);
}
for (int i = (p.getx () / 3) * 3; i < (p.getx () / 3) * 3 + 3; i++)
for (int j = (p.gety () / 3) * 3; j < (p.gety () / 3) * 3 + 3; j++)
if (val[i][j] != 0 && p.getpos (val[p.getx ()][i]) == 0)
p.setpos (val[i][j], 1);
/*寻找可行解*/
int found = 0;
for (int i = 1; i < 10; i++)
if (p.getpos(i) == 0) { //找到一可行解
found = 1;
val[p.getx ()][p.gety ()] = i;
p.setpos (i, 1);
pset.del (iz);
if (pset.isEmpty()) {
write (fpw);
return 1;
}
if (dfs ()) //找下一个空位的可行解
return 1;
p.setpos (i, 0);
}
return 0;
}
附加题
附加题的解题关键有三,一是交互界面的设计,二是数独题目的生成,三是解题结果的判定。
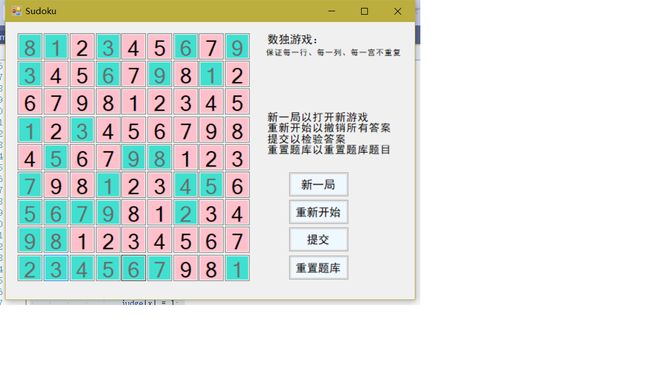
交互界面的设计
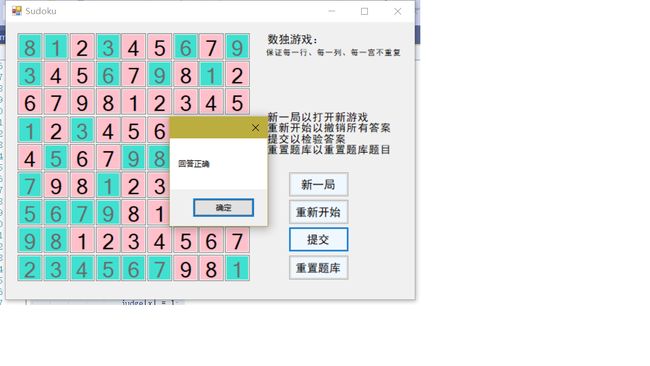
我使用了C#开发Windows窗体应用(.Net Framework),窗体中包含9×9个TextBox以显示数独,以及四个Button分别用以开始新局、重新开始、提交答案以及重置题库。数独TextBox分别用两种显示风格以区分题目和解答(题目与解答不同风格的设计来源于网络),在重置题库题目完成后会有MessageBox提示以及判定题目时会以MessageBox告知答案的正确与否。交互界面美观大方,简约大气。
值得一提的是,设计TextBox的属性使得数独的交互方式可以是鼠标选择或是Tab键选择。
数独题目的生成
对于数独题目的生成,共有两种出题方法,分别为挖洞法和填数法。鉴于已经完成的数独生成器,我采用的是挖空法生成数独题目。而我的第一方案是将数独生成器为GUI提供接口Sudoku类及其成员函数,但由于C++与C#语法的不同,需要对其代码进行大量修改,我放弃了这个方案。我采用的第二个方案是在GUI中创建Sudoku类及其终局生成函数和挖洞函数,并调用以创建数独题目。终局生成函数与数度生成器中相同,而挖洞函数代码如下:
public void puzzle() //生成谜题
{
int max = 60;
int min = 30;
int[] rand = new int[9];
Random rd = new Random();
for (int i = 0; i < 9; i++) //逐宫
{
int imax = max - (8 - i) * 2;
int imin = min - (8 - i) * 9;
if (imin < 2)
imin = 2;
if (imax > 9)
imax = 9;
rand[i] = rd.Next(imin, imax); //该宫内的数量
max -= rand[i];
min -= rand[i];
int[] arrNum = new int[rand[i]];
for (int ir = 0; ir < rand[i]; ir++)
{
Re:
int x = rd.Next(1, 9);
for (int ix = 0; ix < ir; ix++)
{
if (arrNum[ix] == x)
goto Re;
}
arrNum[ir] = x;
val[(i / 3) * 3 + (x - 1) / 3, (i % 3) * 3 + (x - 1) % 3] = 0;
}
}
}
在这个函数中,我设计了随机挖洞的算法。题目要求,挖洞数量要不少于30个,不大于60个,每个宫内的挖洞数量不小于2个。因此,每个宫内的随机的挖洞数量为2~9个,但由于要使剩余的宫内洞数满足要求,定义了imin和imax变量来保存当前宫可挖洞数的最小值和最大值。由此,可以得到当前宫挖洞数量的取值范围,获得rand[i]。接着随机生成rand[i]个1~9之间不重复的随机数,用以表示宫内位置。获得了当前宫和宫内位置,即可生成满足要求的数独题目。
改进
在黑盒测试过程中发现1,000,000个数独题目用时时间长且没有必要,我将题目数量改为100个,用时约为1秒,较为合适。且随机挖洞函数勇士时间较长,我将挖洞函数的时机调整为一部分行交换之间,而不是每一个终局生成后,提高了题目生成的效率,但是却增大了题目的相似性(题目之间行交换)。
解题结果的判定
对于解题结果的判定,我的第一方案是使用数度生成器中检验数度正确性的函数。但是这是没有必要的,因为其一随机挖洞的题目,其解并非唯一,不能与解答后的终局进行对比,其二挖洞数较多,深度优先搜索树层数较大,回溯的步骤也增多,其三与题目生成原因相同,更改dll需要大量时间。我选择的方案是直接判断TextBox的值而不转换为Sudoku类直接进行正确性判断,至于要判断每一行、每一列、每一宫元素填满且无元素重复即可,因此,只需要9×9×9次循环即可。
private void button_submit_Click(object sender, EventArgs e)
{
if (begin == false)
{
MessageBox.Show("未开始游戏");
return;
}
int[,] map = new int[9, 9];
/*检查是否完成*/
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
TextBox text_element = Game_table[i * 9 + j] as TextBox;
if (text_element.Text == "")
{
MessageBox.Show("未完成所有空白");
return;
}
else
map[i, j] = (text_element.Text.ToCharArray())[0] - '0';
}
}
/*没有空白*/
int[] judge = new int[10];
for (int i = 0; i < 9; i++) //逐行
{
for (int j = 1; j <= 9; j++)
judge[i] = 0;
for (int j = 0; j < 9; j++)
{
int x = map[i, j];
judge[x] = 1;
}
for (int k = 1; k <= 9; k++)
{
if (judge[k] != 1)
{
MessageBox.Show("答案错误");
return;
}
}
}
for (int i = 0; i < 9; i++) //逐列
{
for (int j = 1; j <= 9; j++)
judge[i] = 0;
for (int j = 0; j < 9; j++)
{
int x = map[j, i];
judge[x] = 1;
}
for (int k = 1; k <= 9; k++)
{
if (judge[k] != 1)
{
MessageBox.Show("答案错误");
return;
}
}
}
for (int i = 0; i < 9; i += 3) //逐宫
for (int j = 0; j < 9; j += 3)
{
for (int k = 1; k <= 9; k++)
judge[k] = 0;
for (int a = 0; a < 3; a++)
for (int b = 0; b < 3; b++)
{
int x = map[i + a, j + b];
judge[x] = 1;
}
for (int k = 1; k <= 9; k++)
{
if (judge[k] != 1)
{
MessageBox.Show("答案错误");
return;
}
}
}
MessageBox.Show("回答正确");
}
且为了保证其字符的有效性,我再设置TextBox的属性时,使其KeyPress满足CheckKey函数,代码如下:
private void CheckKey(object sender, KeyPressEventArgs e)
{
if (begin == false)
return;
if (e.KeyChar != '\b' && (e.KeyChar < '1' || e.KeyChar > '9'))
e.Handled = true;
}