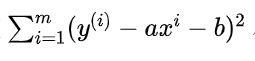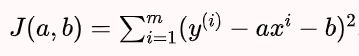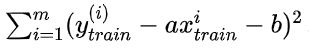0x00 评价模型的好坏
1.数据拆分:训练数据集&测试数据集
2.评价分类结果:精准度、混淆矩阵、精准率、召回率、F1 Score、ROC曲线等
3.评价回归结果:MSE、RMSE、MAE、R Squared
0x01 数据拆分(上篇0x03判断模型好坏 )
0x02 评价分类结果
2.1分类准确度不够
对于极度偏斜(Skewed Data)的数据,只使用分类准确度是不能衡量。需要引入混淆矩阵(Confusion Matrix)做进一步分析。
2.2混淆矩阵(confusion_matrix)
对于二分类问题来说,所有的问题被分为0和1两类,混淆矩阵是2*2的矩阵:
TN:真实值是0,预测值也是0,即我们预测是negative,预测正确了。
FP:真实值是0,预测值是1,即我们预测是positive,但是预测错误了。
FN:真实值是1,预测值是0,即我们预测是negative,但预测错误了。
TP:真实值是1,预测值是1,即我们预测是positive,预测正确了。
因为混淆矩阵表达的信息比简单的分类准确度更全面,因此可以通过混淆矩阵得到一些有效的指标。
2.3 精准率和召回率
精准率(P):precision=TP/(TP+FP) 。精准率分母为所有预测为1的个数,分子是其中预测对了的个数,即预测值为1,且预测对的比例。预测的事件,预测得有多准。
召回率(R):recall=TP/(TP+FN) 。召回率是:所有真实值为1的数据中,预测对的比例 。也就是事件真实发生的情况下,成功预测的比例。
2.4 F1 Score
F1 Score 是精准率和召回率的调和平均值。
数据有偏的情况下,F1 Score是更好的指标。
0x03 ROC曲线
3.1 分类阈值threshold
分类阈值,即设置判断样本为正例的阈值threshold,精准率和召回率这两个指标有内在联系,且相互冲突。precision随着threshold的增加而增加,recall随着threshold的增加而减小。
(在sklearn中有一个方法叫:decision_function,即返回分类阈值)
3.2 TPR
TPR:预测为1,且预测对的数量,占真实值为1的百分比。
TPR=recall=TP/(TP+FN)很好理解,就是召回率。
3.3 FPR
FPR:预测为1,但预测错的数量,占真实值为0的数据百分比。
FPR=FP/(TN+FP)
TPR和FPR之间是成正比的,TPR高,FPR也高。ROC曲线就是刻画这两个指标之间的关系。
3.4 ROC曲线
ROC曲线(Receiver Operation Characteristic Cureve),描述TPR和FPR之间的关系。x轴是FPR,y轴是TPR。
分类阈值threshold取不同值,TPR和FPR的计算结果也不同,最理想情况下,希望所有正例 & 负例 都被成功预测( TPR=1,FPR=0),即 所有的正例预测值 > 所有的负例预测值,此时阈值取 最小正例预测值 与 最大负例预测值 之间的值即可。
TPR越大越好,FPR越小越好,但这两个指标通常是矛盾的。TPR增大,预测更多的样本为正例,同时也增加了更多负例被误判为正例的情况。
两个分类器的ROC曲线交叉,无法判断分类器性能时,可计算曲线下面积AUC,作为性能度量。
3.5 AUC
在ROC曲线中,曲线下面的面积, 称为AUC(Area Under Curve)。AUC的横轴范围(0,1 ),纵轴范围(0,1)所以总面积小于1。
ROC曲线下方由梯形组成,矩形可以看成特征的梯形。因此,AUC的面积可以这样算:(上底+下底)* 高 / 2,曲线下的面积可以由多个梯形面积叠加得到。AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样,模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
0x04 简单线性回归
4.1 简单线性回归
所谓简单,是指只有一个样本特征,即只有一个自变量;所谓线性,是指方程是线性的;所谓回归,是指用方程来模拟变量之间是如何关联的。
4.2 求解思路
找到了最佳拟合的直线方程:y = ax + b,最大程度的拟合样本特征和样本数据标记之间的关系。
4.3 推导思路
所谓的建模过程,其实就是找到一个模型,最大程度的拟合我们的数据。
要想最大的拟合数据,本质上就是找到没有拟合的部分,也就是损失的部分尽量小,就是损失函数(loss function)(也有算法是衡量拟合的程度,称函数为效用函数(utility function)):
思路为:
1.通过分析确定损失函数或者效用函数;
2.通过最优化损失函数或者效用函数,获得机器学习的模型。
近乎所有参数学习算法都是这样的套路,区别是模型不同,建立的目标函数不同,优化的方式也不同。
根据简单线性回归的损失函数,通过最小二乘法(最小化误差的平方)可以求出a、b的表达式:
0x05 最小二乘法
5.1 损失函数的“风险”
5.1.1 损失函数
在机器学习中,所有的算法模型其实都依赖于最小化或最大化某一个函数,称之为“目标函数”。
损失函数描述了单个样本预测值和真实值之间误差的程度。用来度量模型一次预测的好坏。
损失函数是衡量预测模型预测期望结果表现的指标。损失函数越小,模型的鲁棒性越好。
常用损失函数有:
0-1损失函数:用来表述分类问题,当预测分类错误时,损失函数值为1,正确为0
平方损失函数:用来描述回归问题,用来表示连续性变量,为预测值与真实值差值的平方。(误差值越大、惩罚力度越强,也就是对差值敏感)
绝对损失函数:用在回归模型,用距离的绝对值来衡量
对数损失函数:是预测值Y和条件概率之间的衡量。事实上,该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是:在当前模型的基础上,对于样本X,其预测值为Y,也就是预测正确的概率。由于概率之间的同时满足需要使用乘法,为了将其转化为加法,我们将其取对数。最后由于是损失函数,所以预测正确的概率越高,其损失值应该是越小,因此再加个负号取个反。
以上损失函数是针对于单个样本的,但是一个训练数据集中存在N个样本,N个样本给出N个损失,如何进行选择就引出了风险函数。
5.1.2 期望风险
期望风险是损失函数的期望,用来表达理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。又叫期望损失/风险函数。
5.1.3 经验风险
模型f(X)关于训练数据集的平均损失,称为经验风险或经验损失。
其公式含义为:模型关于训练集的平均损失(每个样本的损失加起来,然后平均一下)
5.1.4 经验风险最小化和结构风险最小化
期望风险是模型关于联合分布的期望损失,经验风险是模型关于训练样本数据集的平均损失。根据大数定律,当样本容量N趋于无穷时,经验风险趋于期望风险。
因此很自然地想到用经验风险去估计期望风险。但是由于训练样本个数有限,可能会出现过度拟合的问题,即决策函数对于训练集几乎全部拟合,但是对于测试集拟合效果过差。因此需要对其进行矫正:
结构风险最小化:当样本容量不大的时候,经验风险最小化容易产生“过拟合”的问题,为了“减缓”过拟合问题,提出了结构风险最小理论。结构风险最小化为经验风险与复杂度同时较小。
通过公式可以看出,结构风险:在经验风险上加上一个正则化项(regularizer),或者叫做罚项(penalty) 。正则化项是J(f)是函数的复杂度再乘一个权重系数(用以权衡经验风险和复杂度)
5.1.5 小结
1、损失函数:单个样本预测值和真实值之间误差的程度。
2、期望风险:是损失函数的期望,理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。
3、经验风险:模型关于训练集的平均损失(每个样本的损失加起来,然后平均一下)。
4、结构风险:在经验风险上加上一个正则化项,防止过拟合的策略。
5.2 最小二乘法
5.2.1 最小二乘法
对于测量值来说,让总的误差的平方最小的就是真实值。(这基于,如果误差是随机的,应该围绕真值上下波动。)
正好是算数平均数(算数平均数是最小二乘法的特例)。
这就是最小二乘法,所谓“二乘”就是平方的意思。
(高斯证明过:如果误差的分布是正态分布,那么最小二乘法得到的就是最有可能的值。)
5.2.2 线性回归中使用最小二乘法
找到a和b,使得损失函数尽可能的小。
最终我们通过最小二乘法得到a、b的表达式:
0x06 线性回归算法的衡量标准
简单线性回归的目标是:
对于训练数据集合来说,
尽可能小。
得到a和b之后,将测试集代入a、b中,可以使用
作为衡量回归算法好坏的标准。
(但是这里有一个问题,这个衡量标准是和m相关的。在具体衡量时,测试数据集不同将会导致误差的累积量不同。)
6.1均方误差MSE
测试集中的数据量m不同,因为有累加操作,所以随着数据的增加 ,误差会逐渐积累;因此衡量标准和 m 相关。为了抵消掉数据量的形象,可以除去数据量,抵消误差。通过这种处理方式得到的结果叫做 均方误差MSE(Mean Squared Error):
6.2 均方根误差RMSE
但是使用均方误差MSE收到量纲的影响。例如在衡量房产时,y的单位是(万元),那么衡量标准得到的结果是(万元平方)。为了解决量纲的问题,可以将其开方(为了解决方差的量纲问题,将其开方得到平方差)得到均方根误差RMSE(Root Mean Squarde Error):
6.3 平均绝对误差MAE
对于线性回归算法还有另外一种非常朴素评测标准。要求真实值与 预测结果之间的距离最小,可以直接相减做绝对值,加m次再除以m,即可求出平均距离,被称作平均绝对误差MAE(Mean Absolute Error):
在之前确定损失函数时,我们提过,绝对值函数不是处处可导的,因此没有使用绝对值。但是在评价模型时不影响。因此模型的评价方法可以和损失函数不同。
0x07 更好用的R Square
RMSE和MAE得到的是误差,没有分类准确率(0-1之间取值)的性质,有这样的局限性,引入新的指标R Squared解决。
R Squared:
分子:预测值和真实值之差的平方和,即使用我们的模型预测产生的错误。
分母:是均值和真实值之差的平方和,即认为“预测值=样本均值”这个模型(Baseline Model)所产生的错误。
使用Baseline模型产生的错误较多,使用自己的模型错误较少。因此用1减去较少的错误除以较多的错误,实际上是衡量了我们的模型拟合住数据的地方,即没有产生错误的相应指标。
结论:
R^2 < 0,说明学习模型不如基准模型。此时,数据很有可能不存在任何线性关系;
R^2 = 0,预测模型等于基准模型;
R^2越大也好,越大说明减数的分子小,错误率低;
R^2 = 1,预测模型不犯任何错误;
R^2 <= 1。
0x08 《机器学习》补充
8.1 分类
8.1.1P-R图
P-R图显示模型在样本总体上的查全率(R),查准率(P),在比较时若一个模型的P-R曲线被另一个模型的曲线完全“包住”,则可断言后者性能优于前者。
P-R曲线发生交叉时,比较曲线下面积或“平衡点”BEP(Break-Even Point)“查准率=查全率”时的取值。
8.1.2 多个二分类混淆矩阵
在个混淆矩阵分别计算P,R值,在计算平均,得“宏查准率”(macro-P),“宏查全率”(macro-R),“宏F1”(macro-F1),基于对应元素平均,得“微查准率”(micro-P),“微查全率”(micro-R),“微F1”(micro-F1)。
8.1.3 非均等代价(unequal cost)
权衡不同类型错误造成的不同损失。“代价矩阵”(cost matrix)cost01>cost10,表示真0预1损失程度大于真1预0。
非均等代价下,ROC曲线不能直接反映模型期望总体代价,而“代价曲线”可以。
8.1.4 偏差、方差、噪声
偏差度量了算法的期望与真实值的偏离程度,刻画算法本身的拟合能力;方差度量同样大小的训练集的变动导致学习性能的变化,刻画数据扰动造成的影响;噪声表达当前任务上任何学习算法所能达到的期望泛化误差下界,刻画任务本身的难度。偏差-方差分解说明,泛化性能是由算法的能力、数据充分性、任务本身难度所共同决定的。
0xFF 总结
线性回归的评价指标与分类的评价指标有很大的不同:
评价分类结果:
准确度(简单常用情况)、
混淆矩阵(处理极度偏斜的数据)、
精准率(关注预测中,正确的比例)、
召回率(关注事件发生的情况下,成功预测的比例)、
F1 Score(精准率和召回率的调和平均值)、
ROC曲线(分类阈值、召回率TPR、负例中误判比例FPR、曲线下面积AUC)等
评价回归结果:
均方误差MSE(预测值与真实值之差的平方和,再除以样本量)、
均方根误差RMSE(为了消除量纲,将MSE开方)、
平均绝对误差MAE(预测值与真实值之差的绝对值,再除以样本量)、
以及R方(用1减去较少的错误除以较多的错误,实际上是衡量了我们的模型拟合住数据的地方,即没有产生错误的相应指标)。
参考阅读:
1.《机器学习的敲门砖:kNN算法(中)》(上周已阅)
2.《评价分类结果(上):混淆矩阵、精准率、召回率》
3.《评价分类结果(下):F1 Score、ROC、AUC》
4.《模型之母:简单线性回归&最小二乘法》
5.《模型之母:简单线性回归的代码实现》
6.《模型之母:线性回归的评价指标》
7.《机器学习》周志华著,第2章 模型评估与选择(P23)
代码另附。