求n个数中第k大的数_leetcode从入门到放弃1:第 188 场周赛(20200510)C++、python
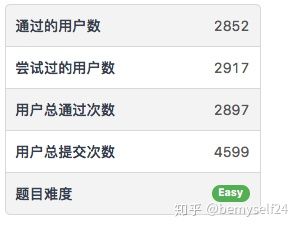
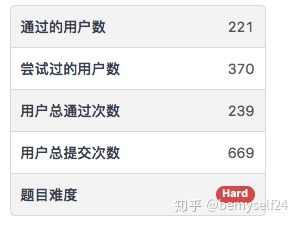
第一次参加leetcode周赛,记录一下吧。后面还贴出了通过的人数,大家也好看看自己处于哪个水准(有点虐心。。。)
1441.用栈操作构建数组
给你一个目标数组 target 和一个整数 n。每次迭代,需要从 list = {1,2,3..., n} 中依序读取一个数字。请使用下述操作来构建目标数组 target :
Push:从 list 中读取一个新元素, 并将其推入数组中。
Pop:删除数组中的最后一个元素。
如果目标数组构建完成,就停止读取更多元素。题目数据保证目标数组严格递增,并且只包含 1 到 n 之间的数字。请返回构建目标数组所用的操作序列。题目数据保证答案是唯一的。
class Solution {
public:
vector buildArray(vector& a, int n) {
int m = a.size();
int cur = 0;
vector ret;
vector tmp;
set H(a.begin(), a.end());
for (int i = 1; i <= n; ++ i)
{
ret.push_back("Push");
tmp.push_back(i);
if (!H.count(i))
{
ret.push_back("Pop");
tmp.pop_back();
}
if (tmp.size() == a.size()) break;
}
return ret;
}
};
题解:从1到n循环,每次判断target中是否存在i,若存在,则直接push(添加“Push”);若不存在,则先push后pop(添加“Push”,“Pop”)
1442.形成两个异或相等数组的三元组数目
给你一个整数数组 arr 。
现需要从数组中取三个下标 i、j 和 k ,其中 (0 <= i < j <= k < arr.length) 。
a 和 b 定义如下:
a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]
注意:^ 表示 按位异或 操作。
请返回能够令 a == b 成立的三元组 (i, j , k) 的数目
class Solution {
public:
int countTriplets(vector& a) {
int n = a.size();
vector s(n+1);
for (int i = 1; i <= n; ++ i)
s[i] = s[i-1]^a[i-1]; //求前i个数的异或结果
int ret = 0;
for (int i = 1; i <= n; ++ i)
for (int j = i+1; j <= n; ++ j)
for (int k = j; k <= n; ++ k)
{
if ((s[j-1]^s[i-1]) == (s[k]^s[j-1])) ret ++; // s[j-1]^s[i-1] 等于第[i, j-1]个数的异或结果
}
return ret;
}
};
题解:这一题考的是异或的性质,相等的两个数异或之后等于0,可以认为是相消。s[j-1]^s[i-1],前a[0]到a[i-1]个数异或之后抵消了。
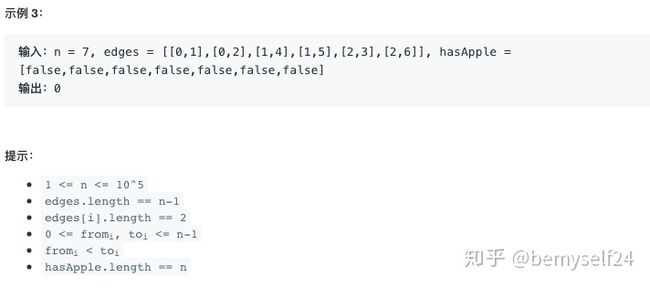
1443.收集树上所有苹果的最少时间
给你一棵有 n 个节点的无向树,节点编号为 0 到 n-1 ,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从 节点 0 出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。无向树的边由 edges 给出,其中 edges[i] = [fromi, toi] ,表示有一条边连接 from 和 toi 。除此以外,还有一个布尔数组 hasApple ,其中 hasApple[i] = true 代表节点 i 有一个苹果,否则,节点 i 没有苹果。
题解:
(1)要收集到所有苹果, 充要条件是每个有苹果的节点都要走一遍;
(2)对于那些本身没有苹果, 且子树没有苹果的节点, 完全不需要走到它们;
(3)所以如果能够统计出所有自身或者子树有苹果的节点, 然后把这些节点都走一遍, 就是最优方案:假设节点数为 n, 由于题目是个树, 所以这些节点构成的路径数目是 n-1, 最优情况就是每个路径走 2 次, 一来一回, 结果就是 2*(n-1);
(4)如何求自身或者子树有苹果的节点呢? 可以想到使用递归, 结果返回当前节点及子树是否有苹果, 然后逐层上去即可。
python解法:
class Solution:
def minTime(self, n: int, edges: List[List[int]],
hasApple: List[bool]) -> int:
# 初始化路径
maps = collections.defaultdict(list)
for e in edges:
maps[e[0]].append(e[1])
def dfs(i):
selfOrChildHasApple = hasApple[i]
for nex in maps[i]:
selfOrChildHasApple |= dfs(nex)
if not selfOrChildHasApple:
# 从字典中移除自身或子树都没有苹果的节点
del maps[i]
return selfOrChildHasApple
dfs(0)
# 字典个数即为最终有效节点的个数
# 但是有可能有效节点为0, 所以需要max一下
return max(0, 2 * (len(maps) - 1))C++解法:
class Solution {
public:
int minTime(int n, vector>& edges, vector& hasApple) {
for (auto& entry : edges) {
maps[entry[0]].push_back(entry[1]);
}
hasAppleHelper(0, hasApple);
return maps.empty() ? 0 : 2 * (maps.size() - 1);
}
private:
bool hasAppleHelper(int idx, vector& hasApple) {
bool selfOrChildHasApple = hasApple[idx];
for (auto i : maps[idx]) {
selfOrChildHasApple = hasAppleHelper(i, hasApple) || selfOrChildHasApple;
}
if (!selfOrChildHasApple) {
maps.erase(idx);
}
return selfOrChildHasApple;
}
private:
unordered_map> maps;
};
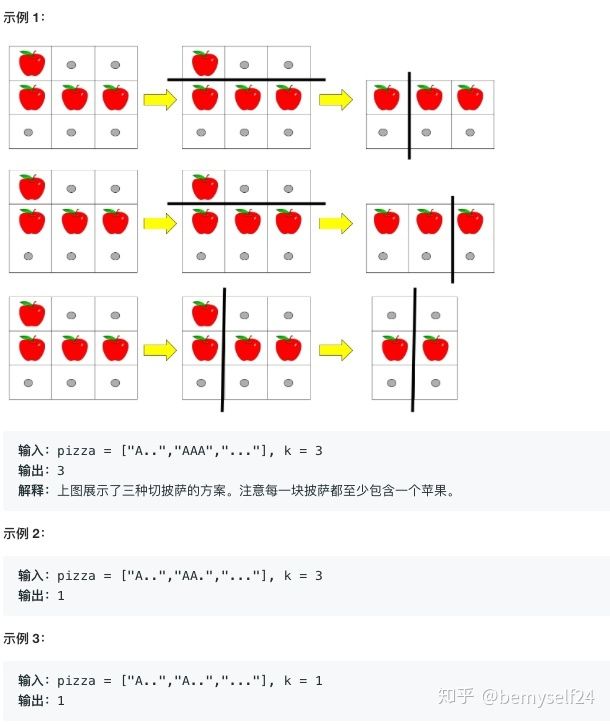
1444.切披萨的方案数
给你一个 rows x cols 大小的矩形披萨和一个整数 k ,矩形包含两种字符: 'A' (表示苹果)和 '.' (表示空白格子)。你需要切披萨 k-1 次,得到 k 块披萨并送给别人。切披萨的每一刀,先要选择是向垂直还是水平方向切,再在矩形的边界上选一个切的位置,将披萨一分为二。如果垂直地切披萨,那么需要把左边的部分送给一个人,如果水平地切,那么需要把上面的部分送给一个人。在切完最后一刀后,需要把剩下来的一块送给最后一个人。请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字,请你返回它对 10^9 + 7 取余的结果。
题目思考
(1)注意到这道题的数据规模很小, 是不是可以利用多个状态记忆化搜索或动态规划?
(2)状态的选择: 每次分出去的都是上面或者左边的, 是否可以利用这一点?
(3)可否通过一些预处理来加速运算呢?
思路
(1)记忆化搜索/动态规划
(2)memo[r,c,p]表示矩形[(r,c), (rows-1, cols-1)](左上,右下坐标,表示前一次切完之后剩下的披萨)分给 p 个人的方案数;
那么 memo[r,c,p] = sum(memo[nexr, c, p-1]) + sum(memo[r, nexc, p-1]):(分别表示下一刀的切法)
r+1<=nexr c+1<=nexc 且[r, nexr)以及[c, nexc]之间的部分必须要有苹果分给当前的人, 否则当前的人就拿不到苹果了 (3)至于怎么求[r, nexr)以及[c, nexc]之间的苹果数, 如果每次递归的时候都重新计算, 那太慢了大概率会超时吧..这部分完全可以通过事先预处理求得 (4)所以额外定义几个字典, rightcnt/downcnt/cnt 分别表示当前坐标右边一行, 下边一列, 以及右下矩形的苹果数目, 右下矩形的苹果数目可以用于剪枝, 当数目<所需人数时直接返回 0 即可 复杂度 (1)时间复杂度 O(rows*cols*k*(rows+cols))): 需要搜索 rows*cols*k 个状态, 而且搜索时要对接下来的 r 或者 c 求和, 根据本题数据量, 就是 50*50*10*100, 还算可以接受 (2)空间复杂度 O(rows*cols*k): memo 的元素个数 python解法: C++解法: 参考资料: (1)力扣class Solution:
def ways(self, pizza: List[str], k: int) -> int:
mod = 10**9 + 7
memo = {}
rightdowncnt = collections.defaultdict(int)
downcnt = collections.defaultdict(int)
rightcnt = collections.defaultdict(int)
rows, cols = len(pizza), len(pizza[0])
# 预处理, 求三种cnt字典,
#分别表示当前坐标右边一行,下面一行,右边或下边矩形的苹果数
for c in range(cols):
for r in range(rows)[::-1]:
downcnt[r, c] = 1 if pizza[r][c] == 'A' else 0
downcnt[r, c] += downcnt[r + 1, c]
#从下往上开始循环,计算下面矩形(水平切法)的苹果数
#这里写的是左下开始循环,但右下循环开始也可
for r in range(rows):
for c in range(cols)[::-1]:
rightcnt[r, c] = 1 if pizza[r][c] == 'A' else 0
rightcnt[r, c] += rightcnt[r, c + 1]
#从右向左开始循环,计算右边矩形(垂直切法)的苹果数
for r in range(rows)[::-1]:
for c in range(cols)[::-1]:
rightdowncnt[r, c] = 1 if pizza[r][c] == 'A' else 0
rightdowncnt[r,c] += rightdowncnt[r + 1, c] + rightcnt[r, c + 1]
#从右下开始循环,
#
def dfs(r, c, p):
# 递归出口
if r == rows or c == cols:
return 0
if (r, c, p) not in memo:
if rightdowncnt[r, c] < p:
# 剪枝
memo[r, c, p] = 0
elif p == 1:
# 只有1人时方案数只能为1
memo[r, c, p] = 1
else:
sm = 0
cnt = 0
# 状态转移, 求接下来所有可能的方案数之和
# 注意取模
for nexr in range(r+1, rows):
cnt += rightcnt[nexr-1, c]
if cnt > 0:
sm = (sm + dfs(nexr, c, p - 1)) % mod
cnt = 0
for nexc in range(c+1, cols):
cnt += downcnt[r, nexc-1]
if cnt > 0:
sm = (sm + dfs(r, nexc, p - 1)) % mod
memo[r, c, p] = sm
return memo[r, c, p]
res = dfs(0, 0, k)
return res
class Solution {
public:
int ways(vector