机器学习系列手记(八):采样之高斯分布采样
采样
高斯分布采样
首先,假设随机变量 z z z 服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),令
x = σ ⋅ z + μ x=\sigma \cdot z + \mu x=σ⋅z+μ
则 x x x 服从均值为 μ \mu μ、方差为 σ 2 \sigma^{2} σ2的高斯分布 N ( μ , σ 2 ) N(\mu, \sigma^{2}) N(μ,σ2)。因此,任意高斯分布都可以由标准正态分布通过拉伸和平移得到,所以这里只考虑标准正态分布的采样。常见的采样方法有逆变换法、拒绝采样、重要性采样、马尔科夫蒙特卡罗采样法等。具体到高斯分布,采样步骤如下。
如果直接使用逆变换法,基本操作步骤为:
(1)产生[0,1]上的均匀分布随机数 μ \mu μ。
(2)令 z = 2 e r f − 1 ( 2 μ − 1 ) z=\sqrt{2}erf^{-1}(2\mu-1) z=2erf−1(2μ−1),则 z z z 服从标准正态分布。其中 e r f ( ⋅ ) erf(\cdot) erf(⋅) 是高分布斯误差函数,它是标准正态分布的累积函数经过简单平移和拉伸变换后的形式,定义如下
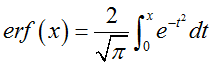
上述逆变换法需要求解 e r f ( x ) erf(x) erf(x) 的逆函数,这并不是一个初等函数,没有显示解,计算起来比较麻烦。所以为了避免这种非初等函数的求逆操作,Box-Muller算法提出了如下解决方案:既然单个高斯分布的累积分布函数不好求逆,那么两个独立的高斯分布的联合分布呢?假设 x , y x,y x,y 是两个服从标准正态分布的独立随机变量,它们的联合概率密度为
p ( x , y ) = 1 2 π e − x 2 + y 2 2 p(x,y)=\frac{1}{2π}e^{-\frac{x^2+y^2}{2}} p(x,y)=2π1e−2x2+y2
考虑 ( x , y ) (x,y) (x,y) 在圆盘 { ( x , y ) ∣ x 2 + y 2 ≤ R … … 2 (x,y)|x^2+y^2≤R……2 (x,y)∣x2+y2≤R……2} 上的概率
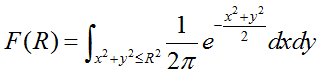
通过极坐标变换将 ( x , y ) (x,y) (x,y) 转化为 ( r , θ ) (r,\theta) (r,θ),可以很容易求得二重积分,上式变为
F ( R ) = 1 − e − R 2 2 F(R)=1-e^{-\frac{R^2}{2}} F(R)=1−e−2R2
这里 F ( R ) F(R) F(R) 可以看成极坐标中 r r r 的累积分布函数。由于 F ( R ) F(R) F(R) 的计算公式比较简单,逆函数也很容易求得,所以可以利用逆变换法来对 r r r 进行采样;对于 θ \theta θ,在 [ 0 , 2 π ] [0,2π] [0,2π]上进行均匀采样即可。这样就得到了 ( r , θ ) (r,\theta) (r,θ),经过坐标变换即可得到符合标准正太分布的 ( x , y ) (x,y) (x,y)。具体采样过程如下:
(1)产生[0,1]上的两个独立的均匀分布随机数 u 1 , u 2 u_1,u_2 u1,u2。
(2)令 x = − 2 l n ( u 1 ) c o s 2 π u 2 , y = − 2 l n ( u 1 ) s i n 2 π u 2 x=\sqrt{-2ln(u_1)}cos2πu_2, y=\sqrt{-2ln(u_1)}sin2πu_2 x=−2ln(u1)cos2πu2,y=−2ln(u1)sin2πu2,则 x , y x,y x,y 服从标准正态分布,并且是相互独立的。
Box-Muller算法由于需要计算三角函数,相对来说还是比较耗时,而Marsaglia polar method则避开了三角函数的计算,因而更快,其具体采样操作如下:
(1)在单位圆盘 { ( x , y ) ∣ x 2 + y 2 ≤ 1 (x,y)|x^2+y^2≤1 (x,y)∣x2+y2≤1} 上产生均匀分布随机数对 ( x , y ) (x,y) (x,y)(在矩形 { ( x , y ) ∣ − 1 ≤ x , y ≤ 1 (x,y)|-1≤x,y≤1 (x,y)∣−1≤x,y≤1} 上利用拒绝采样法即可得到)。
(2)令 s = x 2 + y 2 s=x^2+y^2 s=x2+y2,则 x − 2 l n s s , y − 2 l n s s x\sqrt{\frac{-2lns}{s}}, y\sqrt{\frac{-2lns}{s}} xs−2lns,ys−2lns 是两个服从标准正态分布的样本,其中 x s , y s \frac{x}{\sqrt{s}}, \frac{y}{\sqrt{s}} sx,sy 用来代替Box-Muller算法中的cosine和sine操作。
除了逆变换法,我们还可以利用拒绝采样法,选择一个比较好计算累积分布逆函数的参考分布来覆盖当前正态分布(可以乘以一个常数倍),进而转化为对参考分布的采样以及对样本点的拒绝/接收操作。考虑到高斯分布的特性,这里可以用指数分布来作为参考分布。指数分布的累积分布及其逆函数都比较容易求解。由于指数分布的样本空间为 x ≥ 0 x≥0 x≥0,而标准正态分布的样本空间为 ( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞),因此还需要利用正态分布的对称性来在半坐标轴和全坐标轴之间转化。具体来说,取 λ = 1 \lambda=1 λ=1 的指数分布作为参考分布,其密度函数为
q ( x ) = e − x q(x)=e^{-x} q(x)=e−x
对应的累积分布函数及其逆函数分别为
F ( x ) = 1 − e − x F(x)=1-e^{-x} F(x)=1−e−x
F − 1 ( u ) = − l o g ( 1 − u ) F^{-1}(u)=-log(1-u) F−1(u)=−log(1−u)
利用逆变换法很容易得到指数分布的样本,然后再根据拒绝采样法来决定是否接受该样本,接受的概率为
A ( X ) = p ( x ) M ⋅ q ( x ) A(X)=\frac{p(x)}{M\cdot q(x)} A(X)=M⋅q(x)p(x)
其中 p ( x ) = 2 2 π e − x 2 2 ( x ≥ 0 ) p(x)=\frac{2}{\sqrt{2π}}e^{-\frac{x^2}{2}}(x≥0) p(x)=2π2e−2x2(x≥0) 是标准正态分布压缩到正半轴后的概率密度函数,常数因子M需要满足如下条件:
![]()
实际应用中,M需要尽可能小,这样每次的接受概率大,采样效率更高。因此,可以取

计算后得到接受概率
A ( x ) = e − ( x − 1 ) 2 2 A(x)=e^{-\frac{(x-1)^2}{2}} A(x)=e−2(x−1)2
因此,具体的采样过程如下:
(1)产生[0,1]上的均匀分布随机数 u 0 u_0 u0,计算 x = F − 1 ( u 0 ) x=F^{-1}(u_0) x=F−1(u0) 得到指数分布的样本 x x x。
(2)再产生[0,1]上的均匀分布随机数 u 1 u_1 u1,若 u 1 < A ( x ) u_1
(3)最后再产生[0,1]上的均匀分布随机数 u 2 u_2 u2,若 u 2 < 0.5 u_2<0.5 u2<0.5,则将 x x x 转化为 − x -x −x,否则保持不变;由此最终得到标准正态分布的一个样本。
拒绝采样法的效率取决于接受概率的大小:残奥分布与目标分布越接近,则采样效率越高。还有一种更高效率的拒绝采样算法,叫Ziggurat算法,该算法的本质也是拒绝采样,但采用多个阶梯矩形来逼近目标分布。