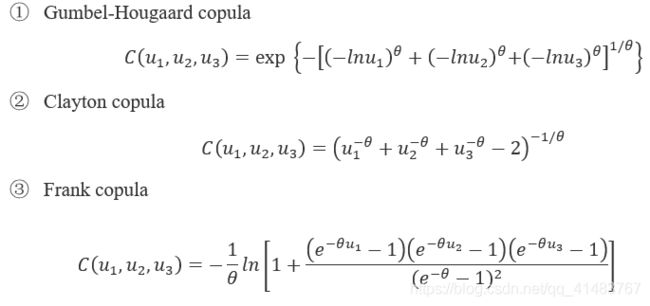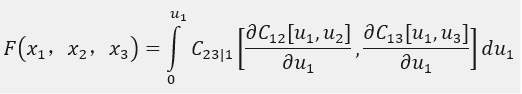【自学笔记】三维copula的构建与分布函数的求解
1.导入所要求解的数据
一般来说不加载额外的包情况下只能导入csv文件,若要导入excel文件可以加载包readxl。我一般是直接用csv文件的。
#加载所需要的包#
library("copula")
library("copBasic")
library("CDVine")
library("VineCopula")
#导入数据#
shuju<-read.csv("D:/QQ文件/z1z2z3.csv")
2.数据处理:转成伪观测值,可以简单地理解为单变量经验分布函数
#得到伪观测值#
emp<-pobs(shuju)
#先大概看下他们之间的相关系数(这里用kendall)
round(cor(U3, method="kendall"), 3)#基本都是强正相关关系
3.三维copula选取、参数估计及分布函数计算
(1)三维copula函数
一般三维copula都构造方法有很多,常见的有对称Archimedeam Copula,非对称Archimedeam Copula。其中非对称构造又包括嵌套Archimedeam copula,pair-copula几种方法。前面两个可以写出显式计算公式。对称Archimedeam Copula要求解高维密度函数需要计算高维偏导数,pair-copula的构造一般没有办法写出显式公式,计算联合分布的时候需要用数值积分求解。
(2)对称Archimedeam Copula(单参数三维copula)
相应的参数估计、拟合优度检验以及分布函数的计算代码:
#单参数copula(以normalcopula为例)---三维对称
fit1<-fitCopula(normalCopula(dim=3), emp, method="mpl")
fit2<-fitCopula(gumbelCopula(dim=3), emp, method="mpl")
fit3<-fitCopula(claytonCopula(dim=3), emp, method="mpl")
fit4<-fitCopula(tCopula(dim=3), emp, method="mpl")
#显示参数估计值、标准误差以及极大似然值
summary(fit1);summary(fit2);summary(fit3);summary(fit4)
#拟合优度检验
gofCopula(normalCopula(dim=3),emp,N=1000,simulation="mult")#p值大于0.05即可
#计算C(U1,U2,U3),举个例子
cop<-normalCopula(dim=3,param =0.96)
#求解分布函数
pCopula(c(0.4,0.4,0.5),copula=cop)
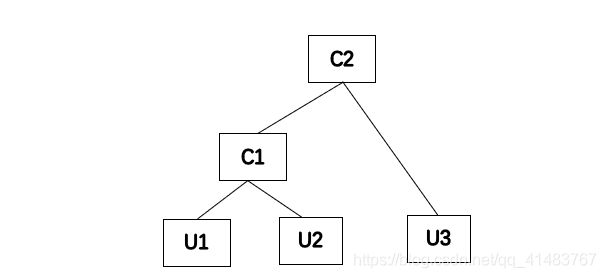
(3)计算嵌套copula(包括完全嵌套和部分嵌套)
不过对于三维来说,完全嵌套和部分嵌套是一样的,基本原理就是先算二维的C1,然后将C1作为新的单变量与第3个向量再联结得到C2,大概是这样的,可以去看看宋松柏的书。
这个的话,代码就和二维是一样的,就是用二维的情况去估计参数择优什么的,得到C1,C2,计算分布概率的时候就是直接一步步算。
#完全嵌套copula函数
BiCopEstList(emp[,1],emp[,2])#选gumbel并得到相应参数
BiCopGofTest(emp[,1],emp[,2],family = 4)#拟合优度检验
V1<-BiCopCDF(emp[,1],emp[,2],family = 4,par=4.92)#得到C1的值
BiCopEstList(V1,emp[,3])#选gaussian
V2<-BiCopCDF(V1,emp[,3],family = 1,par=0.95)#得到C2的值
(4)Pair-copula(这个会比较复杂,一般是树结构)
这个我目前了解的是C-Vine和D-Vine,最早的也有R-Vine,对于三维情况的话,C-Vine和D-Vine是一样的,他们的参数估计有逐步估计(sequential estimates)的也有一步估计的,一般来说,逐步估计就已经阔以满足要求的(参考文献:Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine)
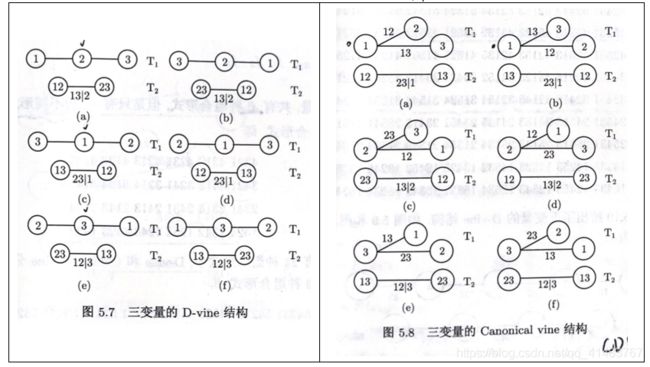
他们的构造情况是这样的:
对于第一层(也就是所谓的Tree 1)就是常见的二维copula,以三维为例,组合形式阔以是321,312,231三种,因为123和321是一样的,都是构造12,23,然后再计算条件分布。这块可能不容易理解,阔以看看参考文献。
接着到第二层(Tree 2):构建的copula是基于条件概率C1|2和C3|2构建的。即表征的是这两种条件概率的联结关系,记作C1,3|2。
#考虑pair-copula
#对于特定的copula函数
d<-3
fam <- rep(4,d*(d-1)/2)#假设三个都是gumbel
# sequential estimation
fit5<-CDVineSeqEst(emp,fam,type=1,method="mle")
CDVineSeqEst(emp,fam,type=1,method="mle")$par
#或者根据AIC准则直接选取最优
CDVineCopSelect(emp,familyset =c(1,2,3,4,5) ,type=1,selectioncrit = "AIC")
#画树图可以看到构造情况
CDVineTreePlot(emp,family = c(4,4,4),tree=1,type = 1)
#看AIC\BIC
par1<-CDVineSeqEst(emp,fam,type=1,method="mle")$par
CDVineAIC(emp,c(4,4,4),par1,type=1)#
CDVineBIC(emp,c(4,4,4),par1,type=1)
#因为CDVine里面没有gof检验,所以转换成RVine,然后用VinCopula里面的包检验
RVM <- C2RVine(c(1,2,3), c(4,4,4), par1, c(0,0,0))
RVineGofTest(emp,RVM,method="ECP")
▶ 接下来是计算分布函数(这个比较复杂)
通过一系列计算简化大概可以化成这个式子:
这样的话就要计算二维的偏导数,然后再对其进行积分。
①求偏导
首先,求偏导的话,目前,会Gumbel copula 和Clayton Copula,以及Frank copula的计算:
#先写一个gumbel copula函数的偏导数function:
"GHcop.derCOP" <- function(u, v, para=NULL, ...)
{
x <- -log(u); y <- -log(v)
A <- exp(-(x^para + y^para)^(1/para)) * (1 +(y/x)^para)^(1/para - 1)
return(A/u)
}
#求解偏导数直接用上面的函数套进去就好了,假设两个偏导均是gumbel
for(i in 1:n)
{
V1[i]<-GHcop.derCOP(u=emp[i,1],v=emp[i,2],para = 4.920055 )
V2[i]<-GHcop.derCOP(u=emp[i,1],v=emp[i,3],para=4.633899)
}
#套个循环,计算出了两个偏导数
②积分
对于积分,我一般用integrate一维函数积分
#自己定义一下积分函数
F1<-function(u1)
{
u2=0.4
u3=0.4
V<-GHcop.derCOP(GHcop.derCOP(u2,u1,para = 4.92),
GHcop.derCOP(u3,u1,para = 4.63),para=1.546397)
}
integrate(F1,0,0.4)#输出的就是C(0.4,0.4,0.4)的值,大概是0.08
#目前的话,只能一个个输出,因为integrate不能对向量进行操作,或者可以再套个循环?我之后再研究下。