- 双调排序介绍 - 炒饭的小站
- 双调排序解答 - CSDN
有一定了解的可以直接看最后一部分的代码。
双调排序是一种并行排序算法。
- 如果以串行的方式运行,其复杂度:O(nlog(n))
- 如果有 n(其实是 n/2) 个可同时运行的线程,则复杂度:O(log(n))。
上面的复杂度是基于输入序列为双调序列。
双调序列
双调序列(Bitonic Sequence) 是指由一个 非严格增序列X 和 非严格减序列Y 构成的序列,任意两个数,都是双调序列。
(非严格指的是可以出现重复元素,或者NaN不参与排序)
定义:一个序列 a1,a2, …,an 是双调序列(Bitonic Sequence),如果:
(1)存在一个 ak(1 ≤ k ≤ n),使得 a1 ≥ … ≥ ak ≤ … ≤ an 成立;或者
(2)序列能够循环移位满足条件(1)
条件(2)非常重要,因为好多序列表面不是,其实是双调的。
双调排序
基本的双调排序只能处理 2^n 个数的序列。
首先定义操作 sortSeq,输出是一个双调序列。
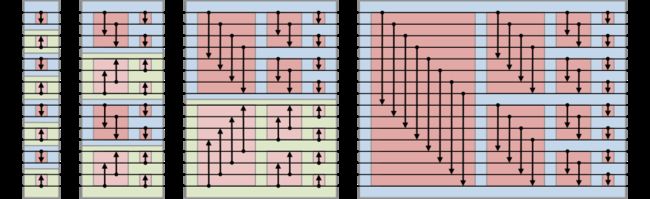
下图中 s 为双调序列,s1 为升序(红),s2 为降序(蓝)。
交换之后,s1 中的序列就是两两比较的较小值,s2 的序列就是两两比较的较大值。本来 s1是升序,s2 是降序的,经过如此操作之后,s1,s2 都是双调的,参考红蓝多边形。在构建 s1 和 s2 时,可以用 n/2 个线程对两两元素进行比较交换,从而实现并行运算。
再对 s1,s2 分别进行 sortSeq 操作,就这样递归操作,直到传入 sortSeq 的序列长度为2,最终 s 就是升序排列的。
下面举个例子说明双调排序过程:
初始值:(10 11 13 14 15 16 17 18, 19 15 13 12 12 11 9 8)
(10 11 13 14 15 16 17 18) (19 15 13 12 12 11 9 8)
网络1排序: (10 11 13 12 12 11 9 8) (19 15 13 14 15 16 17 18)
(10 11 13 12) (12 11 9 8) (19 15 13 14) (15 16 17 18)
网络2排序→ (10 11 9 8) (12 11 13 12) (15 15 13 14) (19 16 17 18)
(10 11) (9 8) (12 11) (13 12) (15 15) (13 14) (19 16) (17 18)
网络3排序→ (9 8) (10 11) (12 11) (13 12) (13 14) (15 15) (17 16) (19 18)
最终结果:(8 9 10 11 11 12 12 13 13 14 15 15 16 17 18 19)
网络2排序的结果中 (12 11 13 12) 经过循环位移之后也是双调序列。
那么如何构建最初的双调序列?
双调排序的初始序列是双调序列,所以对于普通的无序数列要先转换。
算法采用 自底向上 的方法逐步构建双调序列,因为任意两个数都可以视为双调序列。
(1)将无序的输入序列转换成双调序列
对于无序数组 A,相邻的两个数肯定是双调序列,比如 (a0,a1), (a2,a3) 等等
首先步长为 2:(a0,a1) 传入 sortSeq,变成升序序列,
(a2,a3) 传入 sortSeq,变成降序序列,……
然后步长为 4:(a0,a1,a2,a3) 是双调序列,传入 sortSeq 变成升序序列,
(a4,a5,a6,a7) 也是双调的,传入 sortSeq 变成降序序列,……
步长依次为 2^n:
……
最后变为前 n/2 元素是升序,后 n/2 是降序的完整双调序列。
上图中,16个数据,8个比较器,无序数列需要 log(8) = 3 部分完成全局双调序列,步长分别为:20,21,22。理解为 1 增序、2 增序、4 增序。
- 设比较的步长为 s,则比较的层数为 log(s)+1,理解为自顶向下比较的层数
- 每一层都比较 8 次。(8个比较器)
所以比较的总次数为:(1+2+3) * 8 = 48
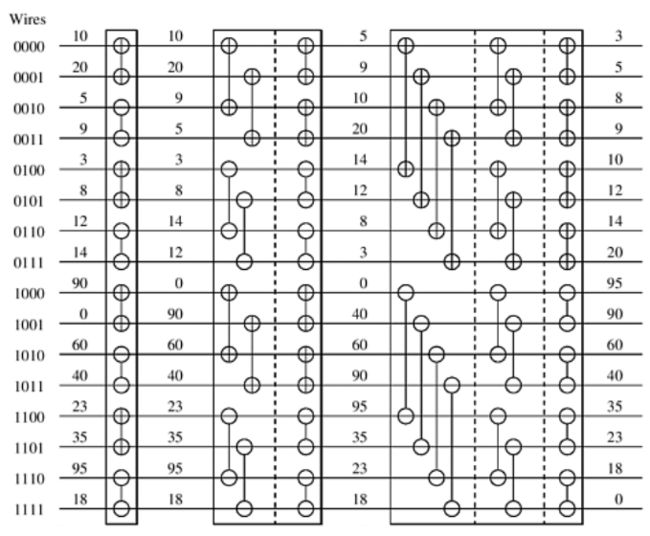
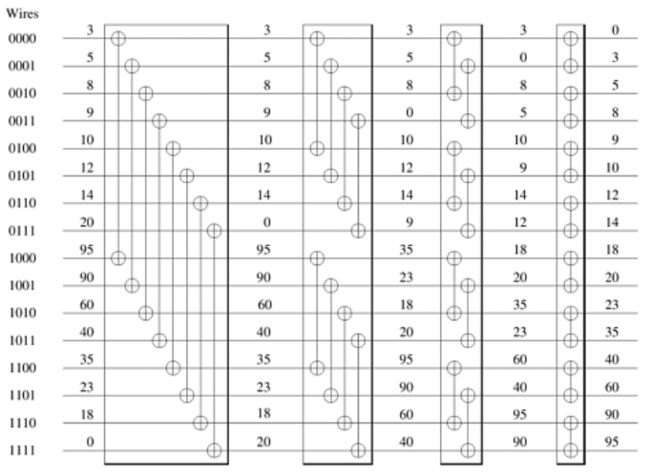
(2)双调序列合并成为有序序列
完整的双调序列传入 sortSeq 变成完整的升序序列。
这一部分,步长为 8,比较层数为 4。
构建双调序列:自底向上
排序双调序列:自顶向下
综上,双调排序比较的总次数为:(1+2+3+4) * 8 = 80
下面的代码分为:
- 基本双调排序(非递归)(2^n)
- 显示排序过程的双调排序(非递归)(2^n)
- 基本双调排序(递归)(2^n)
- 任意双调排序(递归)(任意正数)(真正普适的双调排序)
1. 基本双调排序(非递归)(2^n)
#include
#include
using namespace std;
void printArr(int *arr, int len) {
for (int i = 0; i < len; ++i) {
cout << setw(3) << arr[i];
}
cout << endl << endl;
}
// 双调排序
void bitonicSort(int *arr, int len, bool asd) { // asd 升序
int step = len / 2; // len = 2^k
for (; step > 0; step /= 2) {
for (int i = 0; i < len; i += 2 * step) { // 2 * step 一组序列
for (int j = i; j < i + step; ++j) { // 遍历序列内部,i是序列起点
if (asd) {
if (arr[j] > arr[j + step]) swap(arr[j], arr[j + step]);
} else {
if (arr[j] < arr[j + step]) swap(arr[j], arr[j + step]);
}
}
}
}
}
int main() {
int len = 16;
auto *arr = new int[len]; // 自动识别类型
bool asd = true;
// 1.随机生成无序序列
srand((unsigned int) time(nullptr));
for (int i = 0; i < len; ++i) {
arr[i] = (int) random() % 100;
}
cout << "无序序列: ";
printArr(arr, len);
// 2.将无序的输入序列转换成双调序列
for (int step = 2; step < len; step *= 2) {
for (int i = 0; i < len; i += 2 * step) {
bitonicSort(arr + i, step, asd);
bitonicSort(arr + step + i, step, !asd);
}
}
cout << "双调序列: ";
printArr(arr, len); // 双调序列
// 3.双调序列合并成为有序序列
bitonicSort(arr, len, asd);
cout << "有序序列: ";
printArr(arr, len); // 有序序列
}
无序序列: 26 25 38 50 29 19 91 80 7 46 15 78 19 32 86 66
双调序列: 19 25 26 29 38 50 80 91 86 78 66 46 32 19 15 7
有序序列: 7 15 19 19 25 26 29 32 38 46 50 66 78 80 86 91
2. 显示排序过程的双调排序(非递归)(2^n)
#include
#include
using namespace std;
void printArr(int *arr, int len) {
for (int i = 0; i < len; ++i) {
cout << setw(3) << arr[i];
}
cout << endl << endl;
}
// 双调排序
void sortSeq(int *arr, int len, bool asd) {
int step = len / 2;
for (; step > 0; step /= 2) {
for (int i = 0; i < len; i += 2 * step) {
for (int j = 0; j < step; ++j) {
if (asd) {
if (arr[i + j] > arr[i + step + j]) swap(arr[i + j], arr[i + step + j]);
} else {
if (arr[i + j] < arr[i + step + j]) swap(arr[i + j], arr[i + step + j]);
}
}
}
cout << "步长为: " << step << ", ";
cout << "序列长: " << len << ", ";
printArr(arr, len);
}
}
int main() {
int len = 16;
int *arr = new int[len];
srand((unsigned) time(NULL));
for (int i = 0; i < len; ++i) {
arr[i] = rand() % 100;
}
cout << "初始数据" << endl;
printArr(arr, len);
bool asd = true;
for (int step = 2; step < len; step *= 2) {
for (int i = 0; i < len; i += 2 * step) {
sortSeq(arr + i, step, asd); // 前半升序
sortSeq(arr + i + step, step, !asd); // 后半降序
}
}
cout << "双调序列" << endl;
printArr(arr, len);
sortSeq(arr, len, asd);
cout << "双调排序" << endl;
printArr(arr, len);
}
初始数据
36 15 27 57 4 32 69 46 76 99 21 31 92 31 90 13
# 自底向上的构建过程中也包含了自顶向下的排序过程
步长为: 1, 序列长: 2, 15 36
步长为: 1, 序列长: 2, 57 27
步长为: 1, 序列长: 2, 4 32
步长为: 1, 序列长: 2, 69 46
步长为: 1, 序列长: 2, 76 99
步长为: 1, 序列长: 2, 31 21
步长为: 1, 序列长: 2, 31 92
步长为: 1, 序列长: 2, 90 13
步长为: 2, 序列长: 4, 15 27 57 36
步长为: 1, 序列长: 4, 15 27 36 57
步长为: 2, 序列长: 4, 69 46 4 32
步长为: 1, 序列长: 4, 69 46 32 4
步长为: 2, 序列长: 4, 31 21 76 99
步长为: 1, 序列长: 4, 21 31 76 99
步长为: 2, 序列长: 4, 90 92 31 13
步长为: 1, 序列长: 4, 92 90 31 13
步长为: 4, 序列长: 8, 15 27 32 4 69 46 36 57
步长为: 2, 序列长: 8, 15 4 32 27 36 46 69 57
步长为: 1, 序列长: 8, 4 15 27 32 36 46 57 69
步长为: 4, 序列长: 8, 92 90 76 99 21 31 31 13
步长为: 2, 序列长: 8, 92 99 76 90 31 31 21 13
步长为: 1, 序列长: 8, 99 92 90 76 31 31 21 13
双调序列
4 15 27 32 36 46 57 69 99 92 90 76 31 31 21 13
# 自顶向下完成双调序列的排序
步长为: 8, 序列长: 16, 4 15 27 32 31 31 21 13 99 92 90 76 36 46 57 69
步长为: 4, 序列长: 16, 4 15 21 13 31 31 27 32 36 46 57 69 99 92 90 76
步长为: 2, 序列长: 16, 4 13 21 15 27 31 31 32 36 46 57 69 90 76 99 92
步长为: 1, 序列长: 16, 4 13 15 21 27 31 31 32 36 46 57 69 76 90 92 99
双调排序
4 13 15 21 27 31 31 32 36 46 57 69 76 90 92 99
3. 基本双调排序(递归)(2^n)
根据 01 原则,递归时分治的两段必须 前半降序,后半升序。
#include
#include
using namespace std;
void printArr(int *arr, int len) {
for (int i = 0; i < len; ++i) {
cout << setw(3) << arr[i];
}
cout << endl << endl;
}
// 由bitonicSort中的顺序可知,这里传入的arr已是双调序列
void bitonicMerge(int *arr, int len, bool asd) {
if (len > 1) {
int m = len / 2;
for (int i = 0; i < m; ++i) {
if (arr[i] > arr[i + m] == asd)
swap(arr[i], arr[i + m]); // 根据asd判断是否交换
}
// for循环结束后又生成了2个双调序列,分别merge直到序列长度为1
bitonicMerge(arr, m, asd); // 都是按照asd进行merge
bitonicMerge(arr + m, m, asd);
}
}
void bitonicSort(int *arr, int len, bool asd) { // asd 升序
if (len > 1) {
int m = len / 2;
bitonicSort(arr, m, !asd); // 前半降序
bitonicSort(arr + m, len - m, asd); // 后半升序
// 前2个sort之后形成了1个双调序列,然后传入merge合并成asd规定的序列
bitonicMerge(arr, len, asd); // 合并
}
}
int main() {
int len = 16;
auto *arr = new int[len]; // 自动识别类型
bool asd = true;
// 1.随机生成无序序列
srand((unsigned int) time(nullptr));
for (int i = 0; i < len; ++i) {
arr[i] = (int) random() % 100;
}
cout << "无序序列: ";
printArr(arr, len);
// 2.双调排序
bitonicSort(arr, len, asd);
cout << "双调排序: ";
printArr(arr, len);
}
无序序列: 83 86 77 15 93 35 86 92 49 21 62 27 90 59 63 26
双调排序: 15 21 26 27 35 49 59 62 63 77 83 86 86 90 92 93
4. 任意双调排序(递归)(任意正数)
说说双调排序 - ddppqq - CSDN
递归实现的任意双调排序与基本双调排序区别在于归并部分
// 基本双调排序归并
void bitonicMerge(int *arr, int len, bool asd) {
if (len > 1) {
int m = len / 2;
for (int i = 0; i < m; ++i) {
if (arr[i] > arr[i + m] == asd)
swap(arr[i], arr[i + m]); // 根据asd判断是否交换
}
// for循环结束后又生成了2个双调序列,分别merge直到序列长度为1
bitonicMerge(arr, m, asd);
bitonicMerge(arr + m, m, asd);
}
}
// 任意双调排序归并
void bitonicMergeAnyN(int *arr, int len, bool asd) {
if (len > 1) {
int m = getGreatest2nLessThan(len);
for (int i = 0; i < len - m; ++i) {
if (arr[i] > arr[i + m] == asd)
swap(arr[i], arr[i + m]); // 根据asd判断是否交换
}
bitonicMergeAnyN(arr, m, asd); // 一般情况下,m > len-m
bitonicMergeAnyN(arr + m, len - m, asd);
}
}
对于任意双调排序,因为 len 不一定等于 2^n,所以 m 取 Greatest2nLessThan(len),即在满足 2^n < len 的情况下,n 取最大值时,m = 2^n,对于基本双调排序,len = 2^n,m = len/2 也即为Greatest2nLessThan(len)。
任意双调排序主要思想:
- 首先不断的二分,直到每组只剩下一个元素,然后开始归并。
- 双调排序归并时以不大于 n 的最大 2 的幂次方 2k 为界限,把 2k..n 的元素分别与 0..(n-2k) 的元素比较,然后再分别在0..2k 和 2k..n 这两段上分别应用比较网络。
- 双调排序难以理解的地方就在于这个归并的过程,假设我们要把长度为 n 的序列 arr 升序排列,由于二分时是把前 n/2 的序列降序排列后 n/2 的序列升序排列的,而 n-2k < n/2,所以前 n-2k 和后 n-2k 个元素都大于中间的元素,当前 n-2k 个元素和后 n-2k 个元素比较时,会把序列中最大的 n-2k 个元素放到最后 n-2k 个位置上,也就是说比较后,2k..n 的元素都比 0..2k 的元素大(这一点是确定的,因为前半段递减,后半段递增,比较的时候相当于“极大值”与“极小值”的比较,有点田忌赛马的味道),这样在分别对这两段用同样的方法归并,最终得到完整的升序序列。
双调排序分治的核心理论:任意的正整数都能表示成 2 的幂指数和的形式,其实就是所有的正整数都能用二进制表示。因为序列在不断地拆分成 2 的幂指数的长度。
n = 6, 4+2
n = 7, 4+3 = 4+2+1
n = 8, 4+4
举个例子:
以6个元素的序列为例,前3个元素已经降序排好,后3个元素已经升序排好(递归到底时是从1个元素开始返回的,所以对6个元素归并时前后3个元素已经排好序),这个以4(不大于6的最大2的幂次方)为界限,分别让第1个和第5个、第2个和第6个元素比较,使得这6个元素中最大的两个处于第5、6个位置上,然后再分别对前4个和后2个元素按此方法归并,最终递归完成排序。
然后在 bitonicSort 函数中,只需将 bitonicMerge 改为 bitonicMergeAnyN,另外,bitonicSort 分治的两段长度不一定相等,即 m >= len-m,只有当 len = 2^n 时,m = len-m = len/2,此时任意双调排序实际为基本双调排序。
void bitonicSort(int *arr, int len, bool asd) { // asd 升序
if (len > 1) {
int m = len / 2;
bitonicSort(arr, m, !asd); // 前半降序
bitonicSort(arr + m, len - m, asd); // 后半升序
// 前2个sort之后形成了双调序列,然后传入merge合并成asd规定的序列
// bitonicMerge(arr, len, asd); // 注释掉基本双调排序
bitonicMergeAnyN(arr, len, asd);
}
}
完整代码
#include
#include
using namespace std;
void printArr(int *arr, int len) {
for (int i = 0; i < len; ++i) {
cout << setw(3) << arr[i];
}
cout << endl << endl;
}
int getGreatest2nLessThan(int len) {
int k = 1;
while (k < len) k = k << 1; // 注意一定要加k=
return k >> 1;
}
// 基本双调排序归并
void bitonicMerge(int *arr, int len, bool asd) {
if (len > 1) {
int m = len / 2;
for (int i = 0; i < m; ++i) {
if (arr[i] > arr[i + m] == asd)
swap(arr[i], arr[i + m]); // 根据asd判断是否交换
}
// for循环结束后又生成了2个双调序列,分别merge直到序列长度为1
bitonicMerge(arr, m, asd);
bitonicMerge(arr + m, m, asd);
}
}
// 任意双调排序归并
void bitonicMergeAnyN(int *arr, int len, bool asd) {
if (len > 1) {
int m = getGreatest2nLessThan(len);
for (int i = 0; i < len - m; ++i) {
if (arr[i] > arr[i + m] == asd)
swap(arr[i], arr[i + m]); // 根据asd判断是否交换
}
bitonicMergeAnyN(arr, m, asd); // 一般情况下,m > len-m
bitonicMergeAnyN(arr + m, len - m, asd);
}
}
// 双调排序(基本 + 任意)
void bitonicSort(int *arr, int len, bool asd) { // asd 升序
if (len > 1) {
int m = len / 2;
bitonicSort(arr, m, !asd); // 前半降序
bitonicSort(arr + m, len - m, asd); // 后半升序
// 前2个sort之后形成了双调序列,然后传入merge合并成asd规定的序列
// bitonicMerge(arr, len, asd); // 注释掉基本双调排序
bitonicMergeAnyN(arr, len, asd);
}
}
int main() {
int len = 16;
auto *arr = new int[len]; // 自动识别类型
bool asd = true;
// 1.随机生成无序序列
srand((unsigned int) time(nullptr));
for (int i = 0; i < len; ++i) {
arr[i] = (int) random() % 100;
}
cout << "无序序列: ";
printArr(arr, len);
// 2.双调排序
bitonicSort(arr, len, asd);
cout << "双调排序: ";
printArr(arr, len);
}
无序序列: 83 86 77 15 93 35 86 92 49 21 62
双调排序: 15 21 35 49 62 77 83 86 86 92 93