6.8.5.2经济批量与单件流
内容提要:转移批量可以不等于生产批量,转移批量越小,生产时间越少。单件流的生产总时间最少(不考虑换模时间)。工序总用时=总数×瓶颈用时+批量×非瓶颈用时
高德拉特在《站在巨人的肩膀上》写到:“
我们从福特和大野耐一身上学到的是,不要接受所谓的固定批量。因为经济批量实际上不经济,相反我们应该尽力追求单件流,我们已经深深认识到当我们正在加工一个批量的一件产品时(混合或烘干过程除外),其它的部件都在等待。”我们追求的目标是:改善生产的流动性(等同于前置时间),即追求总工序时间最短。
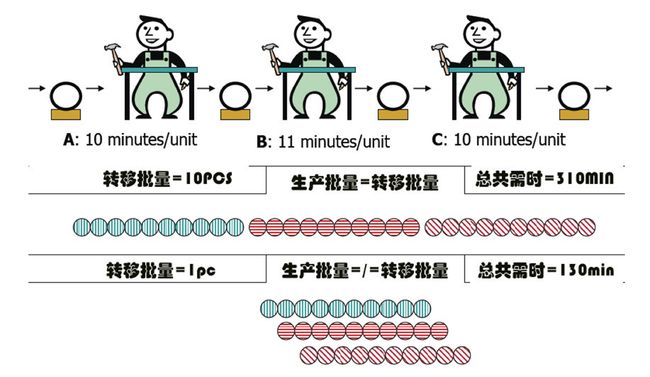
一个生产流程有A、B和C三道工序,速度分别为10分钟/件、11分钟/件和10分钟/件。如果转移批量是10件,批次是1批,那么生产完10件产品需要310分钟。如果转移批量是1件,批次是10批,那么总工序用时是130分钟(如图6-138所示)。
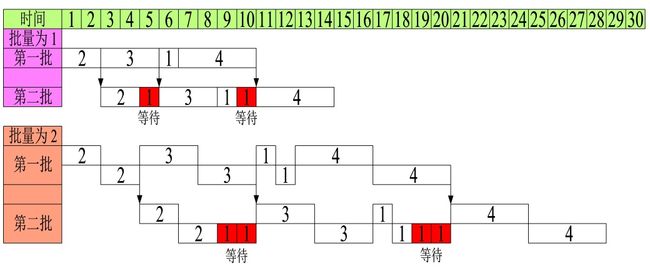
下边我们来推导工序总用时的公式。一个生产流程有4道生产工序,每道工序的速度分别是2分钟/件、3分钟/件、1分钟/件和4分钟/件,工序4是瓶颈(如图6-139所示)。
当批量为1件,批次为2批时,工序1耗时2分钟,工序2耗时3分钟,工序3耗时1分钟,工序4耗时4分钟,第一批耗时10分钟。当工序1生产耗时2分钟完成本道工序工作后,可以接着完成第二批的工序1的工作,耗费2分钟后,工序2正在生产第一批的产品,还需要1分钟才能完成,所以第二批需要等待1分钟。接着第6分钟时,工序2开始生产第二批的产品,花费3分钟,此时工序3已经完成第一批的生产,所以不需要等待,第二批可以直接进行工序3的加工。当工序3加工完第二批时,工序4正在加工第一批产品,还需要1分钟才能完成,所以第二批需要等待1分钟才能进入工序4的生产。生产完2批产品共耗时14分钟,其中等待2分钟(如图6-140所示)。
当转移批量为2件,批次为2批时,第一批耗时20分钟。当工序1生产耗时2分钟完成本道工序工作后,工序1接着生产第一批的第2件产品,第一批在工序1耗时4分钟,然后2件同时转移到工序2进行加工。工序2耗时6分钟完成2件产品的加工,然后顺次将2件产品转移到工序3和工序4,第一批共耗时20分钟完成生产。在工序1完成第一批的2件产品后,接着开始生产第二批的2件产品。当工序1完成第二批的2件产品后,工序2正在加工第一批产品,所以需要等待2分钟才能生产第二批。在对应10分钟的时刻时,工序2开始生产第二批产品,在对应时刻16分钟时完成加工,此时工序3已经完成第一批的生产,第二批可以直接进入工序3进行加工。在对应时刻18分钟时,工序3完成第二批的生产,此时工序4正在加工第一批的产品,所以第二批需要等待2分钟才能进行工序4进行加工。两批产品加工一共耗时28分钟。
当批量是1件,批次是2批时,第2批工序等待差是2分钟,分别在时刻第4分钟和第9分钟时进行了等待(如表6-13所示)。
1、只有2批,每批1件的情况
工序总用时=第一件总用时+第2件累计时间=单件总用时+(第一道工序用时+工序累计等待时差)
2、有多批,每批不只1件的情况
工序总用时=第一批总用时+剩余批次累计等待用时=单件总用时×批量+(第一道工序用时×批量+累计等待时差×批量)×(总批次数-1)
=批量×[单件总用时+(第一道工序用时+工序累计等待时差)×(总批次数-1)]
因为第一道工序用时+工序累计等待时差等于瓶颈用时,所以
工序总用时=批量×[单件总用时+瓶颈工序用时×(总批次数-1)]
=批量×单件总用时+批量×瓶颈工序用时×总批次数-批量×瓶颈工序用时
=批量×单件总用时+总数×瓶颈工序用时-批量×瓶颈工序用时
=批量×(非瓶颈用时+瓶颈工序用时)+总数×瓶颈工序用时-批量×瓶颈工序用时
=总数×瓶颈用时+批量×非瓶颈用时
结论:工序总用时与总数,瓶颈用时,批量和非瓶颈用时有关。在这个式子中,总数,瓶颈工序用时和非瓶颈用时都是常数不变的,只有批量是可以改变的,即工序总用时大小只与批量大小有关。批量越大,工序总用时越多。
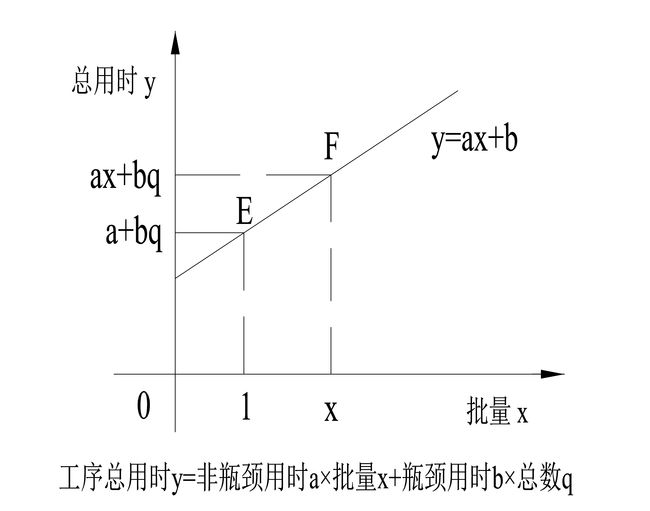
设非瓶颈用时为a,批量为x,瓶颈用时为b,总数为q,瓶颈用时×总数等于bq,为常数不可改。则工序总用时y=ax+bq(如图6-141所示)。(上图中,B工序为瓶颈,A和C为非瓶颈,非瓶颈总用时为20分钟)
工序总用时是一条单调上升的曲线,因为最小的生产批量为1,所以在批量为1时,工序总用时取得最小值为a+bq,当批量为x时,工序总用时随着x的增加而增加,工序总用时等于ax+bq。
如果批量由于某些原因不是最小量1时,随着批量的增加,批量×非瓶颈工序用时也在快速增加,此时工序总用时也在快速增加,如果能减少非瓶颈(生产单件产品的此工序时间)的用时,总工序时间也会相应的减少很多。当然,由于瓶颈用时×总数,每减少瓶颈用时1分钟,相当于减少总数分钟的总用时,瓶颈的变化对总用时影响最大。
结论:瓶颈每减少1单位时间,工序总时间减少总数单位个时间;非瓶颈每减少1单位时间,工序总用时减少批量个单位时间。
当批量变成1时,就和丰田生产方式的一件流“One Piece Flow”是一样的了。TOC与丰田生产方式都是追求缩短生产时间。当一台机器需要生产多种产品且是瓶颈时,则需要经常切换工序,而每次切换是需要花时间的,如果采用一件流时,即批量为1时,总工序用时可能不是最小的,因为切换次数过多。下边我们会推到考虑切换工序时的情况。
在TOC理论中有几条黄金法则,
TOC黄金法则一:瓶颈损失一小时等于整个系统损失一小时。
TOC黄金法则二:非瓶颈节省一小时对整体产出没有任何贡献。
对于这两条法则,如果其中的时间不是指瓶颈和非瓶颈的速度,即如瓶颈工序A速度10分钟/件,非瓶颈工序B速度8分钟/件,而只是指总瓶颈和非瓶颈的工作时间,那么这两条是对的。当瓶颈工作时间由7小时变为8小时,则系统损失1小时;当非瓶颈工作时间由8小时变为7小时,对系统没有影响。
但如果其中的时间是指速度的话,那么第二条法则就错了。作者没找到高德拉特对此的解释,但网上的TOC资料和其中所举的例子都是指生产速度。错误的原因是他们只将总生产用时推导到:
工序总用时=批量×[单件总用时+(第一道工序用时+工序累计等待时差)×(总批次数-1)]
=批量×[单件总用时+瓶颈工序用时×(总批次数-1)]
所以得出错误的结论是:工序总用时与批量,瓶颈工序用时,单件总用时三个变量相关;对总用时的影响为从大到小排列。
如果进一步推到得到:工序总用时=总数×瓶颈用时+批量×非瓶颈用时
所以工序总用时与总数,瓶颈用时,批量及非瓶颈用时有关。当非瓶颈的生产速度提高1分钟时,总工序用时则提高批量个分钟。