《算法导论》读书笔记之红黑树

什么是红黑树？

红黑树是一棵二叉搜索树，它的结点上新增了一个存储位来表示结点的颜色，颜色可以是红或者黑。通过颜色进行约束，确保没有一条路径会比其他路径长出两倍，因此是近似平衡的。

红黑树满足如下五条性质:

1. 每个结点要么是红色，要么是黑色。
2. 根结点是黑色的。
3. 每个叶结点是黑色的。
4. 如果一个结点是红色的，那么它的两个子结点必然是黑色的。
5. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。

** 请注意红黑树的这五点性质非常重要，因为红黑树所有操作都必须满足这五点性质，否则就不能称为红黑树。 **

另外为了简洁和节省空间，我们定义一个叶结点NIL，它的颜色属性为黑，left、right、parent都指向自身且key值没有意义，所有指向叶结点的结点都指向这一个结点，根结点的父亲也指向这个叶结点NIL。下图便是一个简单的红黑树：

image

下面是结点的定义：

public enum Color {RED, BLACK};

    class Node {
        public Node left;
        public Node right;
        public Node parent;
        public int key;
        public Color color;
    }

旋转

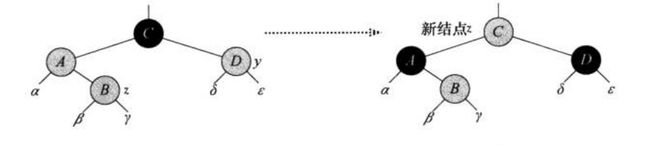
红黑树的插入和删除操作都要借助于旋转，所以这里先讲解下旋转操作。一共有两种旋转：左旋和右旋。当某个结点x在做左旋时，假设它的右孩子是y而不是NIL。左旋以x到y的链为支轴进行。它使y成为子树的新根结点，x成为y的左孩子，y的左孩子成为x的右孩子。并且左旋操作保持了二叉搜索树的性质。右旋操作同理，如下图所示：

image

下面是旋转代码：

public void leftRotate(Node x) {
        if (x == NIL || x.right == NIL) return;
        Node y = x.right;
        x.right = y.left; //将y的左孩子接到x的右结点上
        if (y.left != NIL) {
            y.left.parent = x;
        }
        //使y成为子树的新根结点
        if (x.parent == NIL) {
            root = y;
        } else if (x == x.parent.left) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
        y.parent = x.parent;
        y.left = x; //x接到y的左结点上
        x.parent = y;
    }

    public void rightRatate(Node x) {
        if (x == NIL || x.left == NIL) return;
        Node y = x.left;
        x.left = y.right;
        if (y.right != NIL) {
            y.right.parent = x;
        }
        if (x.parent == NIL) {
            root = y;
        } else if (x.parent.left == x) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
        y.parent = x.parent;
        y.right = x;
        x.parent = y;
    }

红黑树的插入

红黑树的插入思想是新结点以二叉搜索树的性质插入到书中，并且把新节点染成红色,再以新结点往上进行调整使之满足红黑树的性质。下面是红黑树的插入代码：

public void rb_insert(int key) {
        Node newNode = new Node();//包装成新结点
        newNode.key = key;
        newNode.left = NIL;
        newNode.right = NIL;
        newNode.parent = NIL;
        newNode.color = Color.RED;
        //将新结点以二叉搜索树的性质插入到树种
        Node x = root;
        Node y = NIL;
        while (x != NIL) {
            y = x;
            if (key < x.key) {
                x = x.left;
            } else {
                x = x.right;
            }
        }
        newNode.parent = y;
        if (y == NIL) {
            root = newNode;
        } else if (key < y.key) {
            y.left = newNode;
        } else {
            y.right = newNode;
        }
        rb_insert_fixup(newNode); //再对新结点进行调整以满足红黑树的性质
    }

插入操作中性质1和性质3一定不会破坏，另外新结点被染成红色，那么各条路径上的黑结点数量不会变，那么性质5也不会破坏。这样一来，插入操作仅有可能破坏的性质就是2和4。维护性质2很简单，只需要最后将root结点染成黑色。重点就是如何在rb_insert_fixup中维护性质4且不破坏其他性质。这里我们设新结点为z，z父结点p为红色（z父结点为黑时此时已经满足了性质4），z父结点为红色显然z父结点的父结点q不是NIL（根结点为黑色），设p为q的left（p为q的right时可以同理），设y为q的right。rb_insert_fixup主要分为下面三种情况：

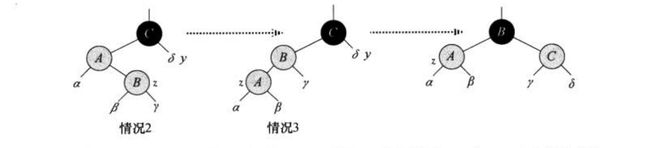
1. z的叔结点也就是y为红色

   
   
   

   image
   
   

   这种情况下，将z父结点和y结点都染成黑色，z父结点的父结点染成红色，此时z父结点的父结点成为新的z。从图中可以看出这个操作并没有破坏原来的性质。新结点z还要再进行三种情况的判断。

2. z的叔结点y是黑色，并且z是父结点的一个右孩子
   这种情况下，z的父结点成为新的z并且以新z进行左旋此时就会转变为情况3进行处理。

3. z的叔结点y是黑色，并且z是父结点的一个左孩子
   

   

   image
   
   这种情况下将z父结点染黑，z父结点的父结点染红并以z父结点进行右旋处理。从图中我们可以看出旋转过程中始终保持了性质5没有被破坏，并且情况3的处理修复了性质4。这样一来就完成了红黑树的插入调整。下面是rb_insert_fixup代码：

private void rb_insert_fixup(Node z) {
        while (z.parent != NIL && z.parent.color == Color.RED) {
            if (z.parent == z.parent.parent.left) {
                Node y = z.parent.parent.right;
                if (y.color == Color.RED) { //情况1
                    y.color = Color.BLACK;
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    z = z.parent.parent;
                } else if (z == z.parent.right) { //情况2
                    z = z.parent;
                    leftRotate(z);
                } else { //情况3
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    rightRatate(z.parent.parent);
                }
            } else {
                Node y = z.parent.parent.left;
                if (y.color == Color.RED) { //情况1 
                    y.color = Color.BLACK;
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    z = z.parent.parent;
                } else if (z == z.parent.left) { //情况2
                    z = z.parent;
                    rightRatate(z);
                } else { //情况3
                    z.parent.color = Color.BLACK;
                    z.parent.parent.color = Color.RED;
                    leftRotate(z.parent.parent);
                }
            }
        }
        root.color = Color.BLACK; //满足红黑树性质2 
    }

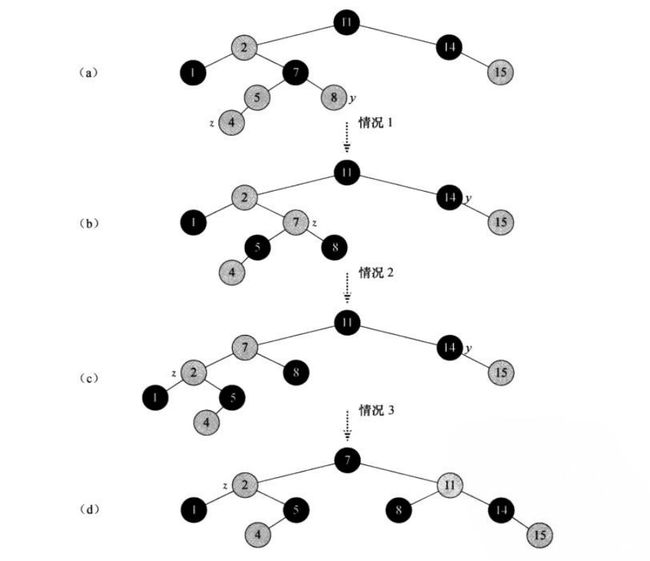
用一个具体实例看下整个调整的流程：

image

a图此时属于情况1，经过调整后7结点成为了新的z继续向上调整。此时z叔结点1已经是黑色并且z是一个右孩子属于情况2，经过情况2的左旋处理后变成了情况3，经过情况3的右旋处理后调整成功，现在满足红黑树的所有性质，又成为了一棵红黑树。红黑树的整个插入过程运行时间为 O（lgn）。

红黑树的删除

红黑树的删除操作比插入更加复杂，也更加不好理解，这里我就写下我自己的理解可能细节方面有些偏差。首先删除操作需要用到子过程rb_transplant，它的作用和二叉搜索树中的transplant相似，只是判断NULL变成了判断NIL叶结点。下面是rb_transplant代码：

private void rb_transplant(Node p, Node q) {
        if (p == NIL) return;
        Node parent = p.parent;
        if (parent == NIL) this.root = q;
        else if (parent.left == p) parent.left = q;
        else parent.right = q;
        if (q != NIL) q.parent = parent;
    }

接下来就是删除操作了，注意红黑树的删除操作是基于二叉搜索树修改的，所以要理解红黑树的删除就必须先理解二叉搜索树的删除。这里我们设要删除的结点为z并且z在树中真实存在。y指向“需要删除的结点”，注意这里"需要删除的结点"意思是逻辑上需要删除的结点，比如：如果z两个孩子结点都不是NIL，那么y会指向z右子树的最小孩子，这是因为我们知道二叉搜索树删除操作中y最终会顶替z成为新的z，我们只需要将y结点的颜色变为z的颜色，这样y就成为了逻辑上要删除的结点。我们设x指向顶替原来y结点的结点，这里有点拗口，解释一下，如果z左孩子是NIL，那么y指向的是z，顶替原来y结点的结点就是z的右孩子所以x指向z的右孩子，如果z两个孩子都不是NIL，那么y会指向z右子树的最小结点，此时顶替原来y结点的结点就是y的右孩子，所以x指向y的右孩子。如果原来y的颜色为红色，那么红黑树的性质全都没有被破坏，完成删除操作。但如果是黑色就要进行调整操作了。下面是删除的代码：

public Node rb_delete(int val) {
        Node z = search(val);
        if (z == NIL) return z; //找到要删除的结点
        Node y = z;
        Node x;
        Color originalColor = y.color;//y会被赋予z的颜色所以要保存原来y的颜色
        f(z.left == NIL) {
            x = z.right;
            rb_transplant(z, z.right);
        } else if (z.right == NIL) {
            x = z.left;
            rb_transplant(z, z.left);
        } else {
            y = z.right;  //z孩子都不是NIL那么y会指向z右孩子的最小结点
            while (y.left != NIL) {
                y = y.left;
            }
            originalColor = y.color;//记得要保存原来y的颜色
            x = y.right;
            if (y != z.right) {
                rb_transplant(y, y.right);
                y.right = z.right;
                z.right.parent = y;
            }
            rb_transplant(z, y);
            y.left = z.left;
            z.left.parent = y;
            y.color = z.color;//z的颜色赋给y，相当于要删除的结点为原来的y
        }
        if (originalColor == Color.BLACK) {//如果原来y为黑色要调整以满足红黑树性质
            rb_deleteFixUp(x);
        }
        return z;
    }

如果原来的y是黑色会有下面三种情况破坏红黑树的性质：

1. 如果删除的是个根结点并且根结点的一个红孩子成为了新根结点，这就不满足性质2，这种情况需要将顶替的结点染成黑色即可。

2. 如果x是红色的并且x的父结点是红色这就不满足性质4，这种情况需要接下来分情况讨论。

3. 在树中移动y，使得任何包含y的简单路径上黑色结点个数少1，这就不满足性质5，这种情况我们可以将现在占有原来y位置的x增加一重额外的黑色（y是没有左孩子的）。这样如果x的颜色为黑色那么它就是双重黑色，如果x的颜色为红色，那么它就是红黑色。这其实破坏了性质1，我们只需要配合旋转，重新染色等调整后将x的颜色变成红色，这时只需将x染黑就满足了性质1，或者x成为根结点，这就相当于移除了一重黑色也就满足了性质1。

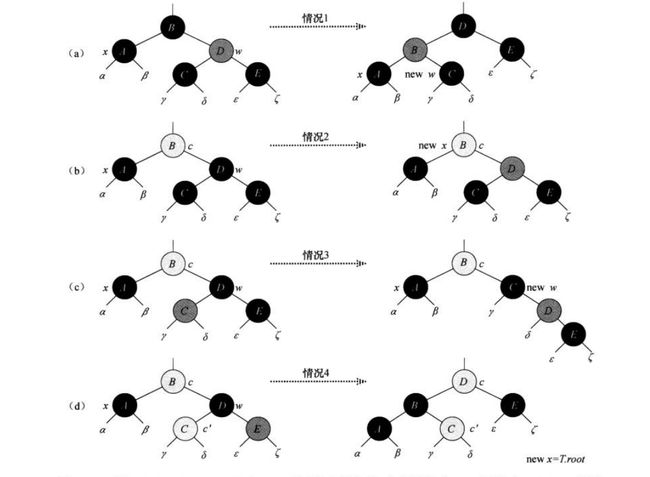
我们设x结点为黑色并且x不是根结点（如果x是红色或者x是根结点只要简单的将x染黑便满足所有性质），c为x的父结点，设x是c的left，w是c的right也就是x的兄弟结点，下面就来分情况讨论：（注意图中黑色代表黑色结点，灰色代表红色结点，白色代表任意红或黑结点）

image

1. x的兄弟结点w为红色
   这种情况下，我们只需要将w染黑将x的父结点染红并且以x的父结点进行左旋，w重新指向x的兄弟结点。这样就将情况1转化为情况2、3或4处理。

2. x的兄弟结点w为黑色，并且w的左右子结点也为黑色
   注意此时x是双重黑色，所以w必然有两个不为NIL的子结点，否则不满足性质5。这种情况下只需将w染红，然后x指向x的父结点，注意到如果新x是红色，那么只要将x染成黑色便已满足所有红黑树性质。

3. x的兄弟结点w为黑色，并且w的左孩子为红色，右孩子为黑色
   这种情况下，我们需要将w染红，w的左孩子染黑然后以w进行右旋，w重新指向x的兄弟结点从而转化为情况4。

4. x的兄弟结点w为黑色，并且w的右孩子为红色
   这种情况下，w赋予c的颜色，c染黑，w的右孩子染黑，再以c进行左旋。从图中便可看出这种情况的处理满足除性质2外的所有性质，所以将x指向root，最终将x染黑便满足了所有性质。

x是父结点的右孩子时同理，至此就完成了整个删除调整操作，以下是删除调整的代码：

private void rb_deleteFixUp(Node x) {
        while (x != root && x.color == Color.BLACK && x != NIL) {
            if (x == x.parent.left) {
                Node w = x.parent.right;
                if (w.color == Color.RED) { //情况1
                    w.color = Color.BLACK;
                    x.parent.color = Color.RED;
                    leftRotate(x.parent);
                    w = x.parent.right;
                }
                if (w.left.color == Color.BLACK && w.right.color == Color.BLACK) {//情况2
                    w.color = Color.RED;
                    x = x.parent;
                } else if (w.right.color == Color.BLACK) { //情况3
                    w.color = Color.RED;
                    w.left.color = Color.BLACK;
                    rightRatate(w);
                    w = x.parent.right;
                }
                if (w.right.color == Color.RED) { //情况4
                    w.color = x.parent.color;
                    w.right.color = Color.BLACK;
                    x.parent.color = Color.BLACK;
                    leftRotate(x.parent);
                    x = root;
                }
            } else {
                Node w = x.parent.left;
                if (w.color == Color.RED) { //情况1
                    w.color = Color.BLACK;
                    x.parent.color = Color.RED;
                    rightRatate(x.parent);
                    w = x.parent.left;
                }
                if (w.left.color == Color.BLACK && w.right.color == Color.BLACK) {//情况2
                    w.color = Color.RED;
                    x = x.parent;
                } else if (w.left.color == Color.BLACK) { //情况3
                    w.color = Color.RED;
                    w.right.color = Color.BLACK;
                    leftRotate(w);
                    w = x.parent.left;
                }
                if (w.left.color == Color.RED) { //情况4
                    w.color = x.parent.color;
                    w.left.color = Color.BLACK;
                    x.parent.color = Color.BLACK;
                    rightRatate(x.parent);
                    x = root;
                }
            }
        }
        x.color = Color.BLACK;
    }

整个删除过程的运行时间为O(lgn)。

总结

花了两天时间终于把红黑树啃完了，大体上算是理解了，可能细节方面有些偏差。理解之后就会发现当初发明红黑树的人是多么的牛X，其实红黑树用途挺广泛的，比如java8的Hashmap中就用到了红黑树，以往冲突部分是链表相连，现在当链表中的结点大于某个值是就采用红黑树存储，这样在冲突较高的场合下效率有了显著的提升。