光学算法-相位提取算法（移相干涉技术PSI）
作者：Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处
注：本文所讲内容为本人硕士毕业论文：《基于干涉图像质量分析的激光干涉仪抗振技术研究》，如有引用需要标注来源哈，如有疑问可以评论回复也可以邮箱[email protected]联系我。
目录
前言
一、移相干涉测量原理
二、四步移相法
三、多步平均法（5-9步）
四、多步解包裹后平均法
前言
自二十世纪末以来，移相干涉技术(Phase Shifting Interferometry, PSI)因其高分辨率、高计算精度的优势，逐渐取代了传统的波面测量技术并被作为一种标准波面测量技术沿用至今。PSI是以光波波长作单位的纳米级超高精度测量手段，通过移相式激光干涉仪实现，被广泛应用在光学领域中，特别是在光学系统成像质量评价和光学器件面形检测方面。
本文介绍了移相干涉技术中最基础却也非常重要的一步——相位提取，主要阐述了移相干涉测量原理、四步移相法提取相位、多步平均法推导过程、多步解包裹后平均法这四个部分，希望能给同样从事该领域研究的你带来一点帮助。
一、移相干涉测量原理
过去的干涉测量技术是通过人的肉眼或者相机拍摄，来直观判断干涉图中条纹特征进而完成测量，该方法的不稳定因素（比如人的主观意志）很多，其精度误差在λ/10左右；现代干涉测量技术通过将电子技术、计算机技术、光电图像处理技术、算法模型和高精度光学元件结合，大大推动了干涉测量领域的发展，使其进入高精度时代。移相干涉技术（PSI）作为现代干涉测量技术的代表，已经成为干涉测量领域学者的研究重点。
移相干涉技术测量的原理：移相式激光干涉仪通过控制压电陶瓷驱动器（PZT）移动参考镜位置或者改变激光器波长的方式，令参考光和测试光的光程差改变，从干涉图像中可看出干涉条纹进行了相应的位移。在移相过程中，通过光电探测器（CCD或者CMOS）采集不同移相量下的干涉图，图1所示为一组移相间隔为90°的移相干涉图组。计算机根据特定的数学算法和模型对干涉图组的像素数据进行系列运算，进而可以求得被测元件的面形信息，并根据计算好的相关参数进行质量评价。
图1 移相间隔为90°的9帧移相干涉条纹图
基于PZT实现移相的过程为：当PZT控制模块发出指定命令时，PZT伸长量进行相应改变，即参考镜和被测镜的相对距离改变，进而完成相位调制以达到移相目的。
在上述移相干涉测量过程中，干涉图像中的条纹分布是由参考光束和测试光束叠加形成的干涉场导致，干涉场的光强信息与干涉图中像素点的灰度信息相关，其分布函数公式(1)可表示为：
 |
(1) |
其中：A(x,y)是干涉图的背景光强，B(x,y)是调制度，
是待测物的波面初始相位信息，
是移相量，(x,y)是干涉图中像素点的坐标信息。
参考镜和被测镜间的面形差P(x,y)与位相分布的关系可表示为公式(2)：
 |
(2) |
λ为激光器波长（本文为He-Ne激光器——632.8nm），在移相干涉测量技术中，测量单位为λ。当通过解相算法处理干涉图组的像素数据，可计算出
，并进一步得到面形信息以完成检测工作。
下面开始介绍3种比较常见和基础的相位提取算法。
二、四步移相法
作为经典的解相算法，四步移相法可以有效计算出理想移相图组的相位分布。先获取无移相的干涉图像，再进行三次移相间隔为π/2的移相，每次移相完成采集1帧图像，共得到4帧相位相差π/2的干涉图像，其图像光强信息分别为：
| (3) |
公式(3)中4个式子进行公式变换消去A和B可得到和四帧图像像素信息的关系式：
| (4） |
该算法求解速度快，适合对理想干涉图组进行求解。当有外部干扰时，相位变化呈无规则态，此时四步移相法的解相效果非常糟糕，无任何抗振能力。与四步移相法类似的单周期定步长算法还有三步算法等。
三、多步平均法（5-9步）
为了抑制移相器线性移相误差或外在环境干扰带来的影响，相关学者在四步移相法的基础上引入了平均技术（本文介绍的平均法基于四步移相法，移相间隔均为π/2）：通过获取T+K（T=4）帧移相间隔为π/2的干涉图像，使干涉图组的相位变化不再局限于一个2π周期内，避免因单周期内干扰过大而导致求解偏差较大的情况发生；鉴于余弦分布的特点，不同周期下干涉图的移相量均可化为单周期移相值，即0、π/2、π、3π/2，每个移相值对应多帧不同周期下的干涉图，对这些干涉图而言，其光强信息在理论上应完全一致，考虑到现实环境干扰的复杂性和无规则性，每帧图的信息都会出现或多或少的偏差，应用平均技术的思想能一定程度上起到减少误差的作用。
基于平均技术思想，多步平均法虽能有效抑制振动干扰，但当帧数过多时，也可能会出现因取图时间过长而引入过量振动的问题。最佳帧数的设置是多步平均法非常关键的一步，综合考虑干涉仪内置相机的性能（如果CCD或CMOS的帧率很高，可以适当增加获取图像的帧数），一般获取9帧图像最佳，既可以保证图组的相位信息跨过两个周期以使平均法达到抑制振动影响的效果，又可以避免引入过量的扰动。
接下来推导九步平均算法的解相公式：
a.将四步移相法公式(4)变形得公式(5)：
| (5） |
上式中，
和
分别代表从第一帧图（即移相量从0开始）开始的4帧干涉图像间解相运算的分子分母部分。四步移相法作为后续平均算法的基本算法式，基础步数为T（=4）。
如果继续获取第五帧图，该干涉图的移相量为2π，化为单周期移相值为0，此时将以第二帧图（即移相量从）开始的4帧干涉图作四步解相运算，可得公式(6)：
| (6） |
将公式(5)和(6)结合可得五步（T+1）平均算法，公式(7)：
| (7） |
b.继续获取第六帧图，该干涉图的移相量为2π+π/2，化为单周期移相值为π/2。同理可获得公式(8)：
| (8） |
此时运用“扩展平均”思想以获得进一步的补偿，即运用N+2的处理方式：分别对前T+1（5）帧和后T+1（5）帧图采用五步平均算法，累加平均得到六步（T+2）平均算法（也可称作扩展平均算法，后文将其统一作平均算法），公式(9)：
| (9） |
c.以此类推，继续扩展可得到T+K步平均算法。
当K=3时，获取到第七帧图，四到七帧图作四步运算得公式(10)：
| (10） |
分别对前T+2（6）帧和后T+2（6）帧作六步平均运算并累加可得七步（T+3）平均算法，公式(11)：
| (11） |
当K=4时，获取到第八帧图，五到八帧图作四步运算得公式(12)：
| (12） |
分别对前T+3（7）帧和后T+3（7）帧作七步平均运算并累加可得八步（T+4）平均算法，公式(13)：
| (13） |
当K=5时，获取到第九帧图，六到九帧图作四步运算得公式(14)：
| (14） |
分别对前T+4（8）帧和后T+4（8）帧作八步平均运算并累加可得九步（T+5）平均算法，公式(15)：
| |
(15） |
至此，九步平均算法的表达式推导完成。
四、多步解包裹后平均法
从上文推导的多步平均算法公式不难看出，多帧图的光强信息权重并不一样，当每帧干涉图均有强度接近的振动干扰时，上述算法能起到一定的误差平衡效果，一旦某帧图像受扰动影响过大，比如(15)式中第四帧图，其高权重系数会导致解相过程受到成倍的振动干扰。
为了解决因权重系数差异大而带来的解相不稳定问题，本文还提出了一种多步解包裹后平均法。设解包裹运算符号为unwrap，对一组帧数为9的干涉图组，从第一帧图开始每4帧图进行一次四步运算得到，K的意义同多步平均法中一致，可得到六组包含不同移相量的相位分布，公式(16)：
| |
(16） |
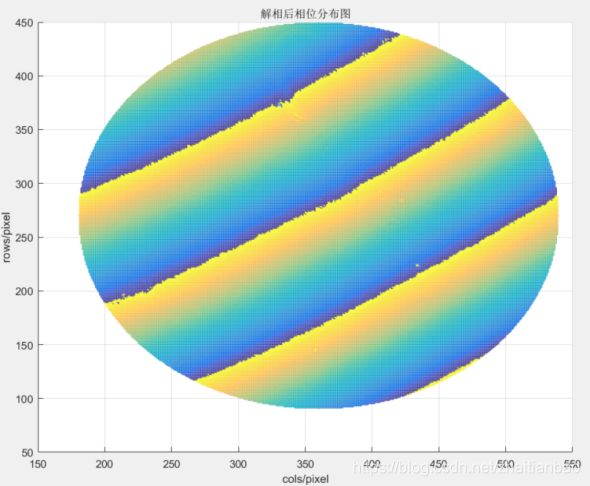
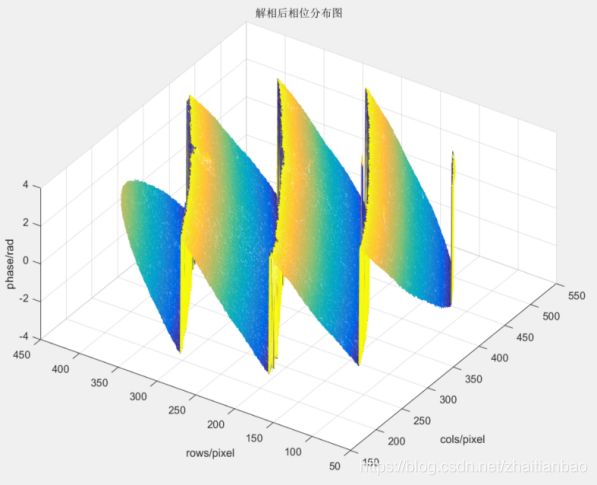
反三角函数arctan通过计算机程序计算得到的区间为单周期（-π，π），因此干涉图的相位分布会出现断层式变化，如图所示是由四帧实际获取的干涉图解相后的相位分布情况，其中图2为二维展示，图3为三维展示。此时的相位分布虽然携带了面形信息，但并非真实的周期性相位信息，因此公式(16)的相位分布无法直接叠加，否则叠加后的相位分布将受到跨周期交错的影响，而呈现异常的波浪式分布，则无法通过解包裹算法还原真实的相位分布。
图2 解相后的相位分布二维
图3 解相后的相位分布三维
为此，将公式(16)的相位分布分别进行解包裹运算，使其还原成真实的相位信息，即相位变化呈连续性而不是断崖式。虽然这六组相位分布的初相信息不一致，但这仅会导致相位的整体平移量变化，而平移量对面形测量而言是无关紧要的。对单组相位分布来说，其变化趋势是相对的且携带面形信息，将六组数据信息直接叠加并取平均，即可获得进行了一定程度误差平衡的真实相位分布
：
 |
(17） |
该算法的优势在于不仅能起到减少误差的作用，还可避免受某帧对应高权重系数的干涉图中振动信息的较强干扰；劣势在于算法的运算效率受解包裹算法效率影响。
注：
1.公式虽多，其实明白了内在逻辑很容易就推出来了，如果想做课题研究，建议自己推一遍，如果有不一样的想法或者思路或者发现我有错误，随时欢迎来找我一起交流，共同进步！
2.后期看情况可能跟大家分享下基于最小二乘原理的迭代算法AIA，这个算法非常不错，应用于现实场景很棒，而不像许多算法仅仅适用于仿真的“漂亮数据”。
3.相位提取算法的代码就不贴了，就是直接将图像矩阵，按照公式的系数加起来再乘除操作就实现了。