数值分析——Newton迭代法求解方程附Matlab程序
Newton迭代法应用
1. 给定初值 x 0 x_{0} x0及容许误差 ε \varepsilon ε,编制Newton法解方程 f ( x ) = 0 f(x) =0 f(x)=0根的通用程序;
Newton 迭代格式的迭代函数为:
φ ( x ) = x − f ( x ) f ′ ( x ) \varphi(x) = x- \frac{f(x)}{f^{\prime}(x)} φ(x)=x−f′(x)f(x)即为 x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_{k}-\frac{f(x_{k})}{f^{\prime}(x_{k})} xk+1=xk−f′(xk)f(xk)
Newton迭代法程序如下:
文件名:Newton.m
x0=1;%初值大小
newton=@(x)x - (x^3/3-x)/(x^2-1); %此处的f(x)=x^3/3-x=0
k=0 ; err=1.000;
phi=10^(-4);%允许误差大小
disp('k x_k err');
while(err>phi)
x1=newton(x0);
err=abs(x1-x0);
x0=x1;
k=k+1;
end
fprintf('%d %1.15f %1.15f\n',k,x1,err);%每次迭代的结果和误差
%输出对于不同初值迭代次数、迭代结果、误差
存在问题:特别对于x=0,时牛顿迭代法可能会失去其作用,并不能通过较小的 δ \delta δ 来找到收敛于0的牛顿序列,导数是否在x=0这一点可导
2. 给定方程 f ( x ) = x 3 − x = 0 f(x)=x^{3}-x=0 f(x)=x3−x=0。容易知道其有三个根 x 1 ∗ = − 3 x_{1}^{*}= - \sqrt3 x1∗=−3, x 2 ∗ = 0 x_{2}^{*} =0 x2∗=0 , x 3 ∗ = 3 x_{3}^{*}= \sqrt3 x3∗=3。
- 由Newton方法的局部收敛法可知:存在 δ > 0 \delta>0 δ>0, 当 δ > 0 \delta>0 δ>0时, Newton迭代序列收敛于根 δ > 0 \delta>0 δ>0,, 是确定尽可能大的 δ > 0 \delta>0 δ>0,;
由牛顿的局部收敛性,即在最大区间 ( x ∗ − δ , x ∗ + δ ) (x^{*}-\delta,x^{*}+\delta) (x∗−δ,x∗+δ)内,通过牛顿迭代,存在收敛序列使得 x n 收 敛 到 x ∗ x_{n}收敛到x^{*} xn收敛到x∗, x ∗ x^{*} x∗= 0 0 0,由区间的对称性可以在 [ 0 , 1 ] [0,1] [0,1]内找到最大的 δ \delta δ ,使得 x n 能 够 收 敛 到 x ∗ x_{n}能够收敛到x^{*} xn能够收敛到x∗
程序如下:
文件名:Converge.m:
max=0.000000;
for i=0:0.0001:1 %将区间按0.0001分割
x1=i; %初值大小
newton=@(x)x - (x^3/3-x)/(x^2-1);%f(x)=x^3/3-x
k=0;err=1.000;
phi=10^(-4); %允许误差大小
while(err>phi)
x2=newton(x1);
err=abs(x2-x1);
x1=x2;
k=k+1;
%fprintf('%d %1.15d %1.15f\n',k,x1,err);
if x1==0
max=i; %记录的最大值
end
end
end
fprintf('max= %1.15f\n',max)
运行程序:
max= 0.774300000000000
由结果可知当误差取 p h i = 1 0 − 4 时 phi=10^{-4}时 phi=10−4时,确定的最大的 δ = 0.77430 \delta=0.77430 δ=0.77430,当 x 0 ∈ ( − 0.77430 , 0.77430 ) 时 x_{0}\in(-0.77430,0.77430)时 x0∈(−0.77430,0.77430)时,Newton迭代序列收敛到根 x 2 ∗ x_{2}^{*} x2∗
- 试取若干初始值, 观察当 x 0 ∈ ( − ∞ , − 1 ) x_{0}\in(-\infty,-1) x0∈(−∞,−1)、 ( − 1 , − δ ) 、 ( − δ , δ ) (-1, -\delta)、(-\delta,\delta) (−1,−δ)、(−δ,δ)、 ( δ , 1 ) 、 ( 1 , + ∞ ) (\delta, 1)、(1,+\infty) (δ,1)、(1,+∞) 时, N e w t o n Newton Newton序列是否收敛以及收敛于那一个根。
分别在 x 0 ∈ ( − ∞ , − 1 ) x_{0}\in(-\infty,-1) x0∈(−∞,−1)、 ( − 1 , − δ ) (-1, -\delta) (−1,−δ)、 ( − δ , δ ) (-\delta,\delta) (−δ,δ)、 ( δ , 1 ) (\delta, 1) (δ,1)、 ( 1 , + ∞ ) (1,+\infty) (1,+∞) 时, N e w t o n Newton Newton,取初值(注意:在取初值时需要修改源程序中的 x 0 x_{0} x0可能在调试中较麻烦,可以建立函数实现输入初值 x 0 x_{0} x0)
A. 在 x 0 ∈ ( − ∞ , − 1 ) 在 x_{0}\in(-\infty,-1) 在x0∈(−∞,−1)内取初值x=-10,利用(1)的Newton.m程序,运行结果:
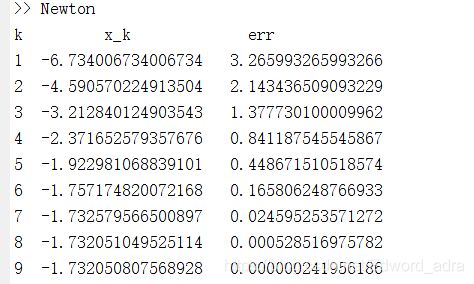
即初值x=-10时,通过9次牛顿迭代可以得到在误差范围内的根,误差为err=0.000000241956186,牛顿序列收敛到 x 1 ∗ = − 3 x_{1}^{*}= - \sqrt3 x1∗=−3
B.在 ( − 1 , − δ ) (-1, -\delta) (−1,−δ)内取初值x=-0.9,利用(1)的Newton.m程序,运行结果:
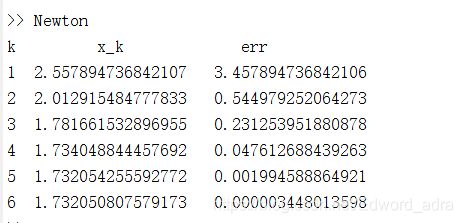
即初值x=-0.9时,通过6次牛顿迭代可以得到在误差范围内的根,误差err=0.000003448013598牛顿序列收敛到 x 3 ∗ = 3 x_{3}^{*}= \sqrt3 x3∗=3
C.在 ( − δ , δ ) (-\delta,\delta) (−δ,δ) 内取初值x=-0.6,利用(1)的Newton.m程序,运行结果:

即初值x=-0.6时,通过4次牛顿迭代可以得到在误差范围内的根,误差err=0.000000341186658。牛顿序列收敛到 x 2 ∗ = 0 x_{2}^{*} =0 x2∗=0
D.在 ( δ , 1 ) (\delta, 1) (δ,1)内取初值x=0.9,利用(1)的Newton.m程序,运行结果:
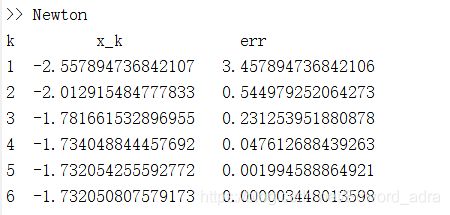
即初值x=0.6时,通过6次牛顿迭代可以得到在误差范围内的根,误差err=0.000003448013598。牛顿序列收敛到 x 3 ∗ = − 3 x_{3}^{*}=- \sqrt3 x3∗=−3
E.在 ( 1 , + ∞ ) (1,+\infty) (1,+∞) 内取初值x=100,利用(1)的Newton.m程序,运行结果:

即初值x=0.6时,通过14次牛顿迭代可以得到在误差范围内的根,误差err= 0.000088593081718。牛顿序列收敛到 x 3 ∗ = 3 x_{3}^{*}= \sqrt3 x3∗=3