李宏毅机器学习笔记(一)——线性回归
文章目录
- 一.什么是回归
- 二.回归的简单例子与步骤
-
- 1.提出问题
- 2.建立函数模型
- 3.评价预估函数的好坏
- 4.如何找到最优参数
- 5.利用测试集对结果进行评估
- 6.重新选择函数模型,进入循环
一.什么是回归
总的来说,其实回归就是一种预测。我们给出了一些已有的数据和对应的结果,然后我们又给出了一些未知结果的数据,然后我们去找出一个函数,去尽量好的得到对应的结果,这其实就是广义上的回归问题。
当然,这个所谓的"函数"可以是任何的函数,因为我们的目标就是得到好的预测结果——注意,是对我们本来不知道结果的数据的预测结果。
二.回归的简单例子与步骤
1.提出问题
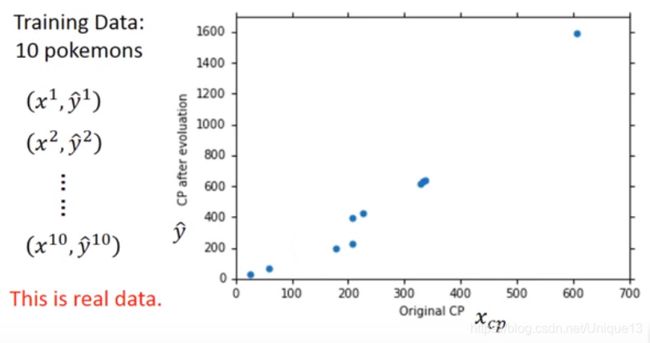
教授的例子十分的有趣,是一个根绝宝可梦进化前的属性去预测宝可梦进化后CP值的问题,因此可见这个函数的输入是对应的数值化的属性,而输出则是预测进化后的CP值。

2.建立函数模型
在这里,老师首先是只考虑了一个特征,并且将收集的数据可视化了。显然通过下面这张图,我们大致可以认为,这应该是线性的,直接引出了线性的模型,也就是让 f ( x ) = w x + b f(x)=wx+b f(x)=wx+b,我们就转化为了寻找最合适的参数 w w w(目前还是数而非向量)和 b b b。
但很多时候,数据维数很大无法可视化,找到函数大致的类型,可能也是很麻烦的事情,而函数的形式是无穷无尽的,我们不可能说用什么方法就肯定就能做出最好的预测。这时我们需要具体问题具体分析,或者是类似"炼丹",按照自己认为不错的模型去评估结果,能找到好结果,那就可以说是合适的模型。
3.评价预估函数的好坏
我们确定了我们的模型(模型本身也可以被称作是一个超参数——“具体为什么选择没什么充分理由,但我就是选了,不改变了”),但是模型内还是有可任意选择的普通参数,例如线性模型的 w w w和 b b b。
对于不同的 w w w和 b b b,显然预测的结果都是不同的,那我们如何去评估参数的好坏呢?因此就要定义一种“损失函数”,这个损失函数把我们的模型函数作为输入,输出所谓的损失值,来说明这个函数有多差。如果我们的预测函数是 f ( x ) f(x) f(x)的话,那这个损失函数就是 L ( f ) L(f) L(f)。当然,至于如何去选,显然我们的选择总要说出一定的道理…我们这里对于回归问题,一般用的都是采用均方误差作为损失函数,也就是对于真实值 ( x i , y i ) (x_i,y_i) (xi,yi)和函数 f ( x i ) = w x + b = y i ^ f(x_i)=wx+b=\hat{y_i} f(xi)=wx+b=yi^,有 L ( f ) = L ( w , b ) = 1 2 ∑ i ( w x i + b − y i ) 2 L(f)=L(w,b)=\frac{1}{2}\sum_i(wx_i+b-y_i)^2 L(f)=L(w,b)=21i∑(wxi+b−yi)2
扩展内容:下面推导该损失函数的合理性:一般来说,对于我们要找的好的预估函数而言,有 y i = w x + b + ϵ y_i=wx+b+\epsilon yi=wx+b+ϵ 其中 ϵ \epsilon ϵ为一个随机扰动项,符合正态分布。之后我们可以用MLE来对参数 w w w和 b b b进行估计: L ( x 1 , x 2 , . . . , x n , w , b ) = ∏ i = 1 n f ( y i ∣ x i ; w ; b ) = ∏ i = 1 n 1 2 π σ e − ( w x i + b − y i ) 2 2 σ 2 L(x_1,x_2,...,x_n,w,b)=\prod_{i=1}^{n}f(y_i|x_i;w;b)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(wx_i+b-y_i)^2}{2\sigma^2}} L(x1,x2,...,xn,w,b)=i=1∏nf(yi∣xi;w;b)=i=1∏n2πσ1e−2σ2(wxi+b−yi)2
取对数,再求对应的最大值,我们可以看出也就是让 ∑ i ( w x i + b − y i ) 2 \sum_i(wx_i+b-y_i)^2 ∑i(wxi+b−yi)2最小,从而得到我们的损失函数;我们在前面乘上二分之一对结果没有影响,仅仅是这样求导后抵消了系数,计算起来更方便。
4.如何找到最优参数
我们已经确定好用平方误差作为损失函数了,那我们接下来的任务就是找到使得损失函数取最小的参数来得到我们最后的预测的模型了。
当然有的时候我们可以用严格的数学推导来计算最优解,但很多时候函数很特殊,无法用公式求解,从而我们就需要使用数值分析这个工具了。
当然这里我们采用其中一种最基础的方法——梯度下降法;更优化的方法会在后面介绍。梯度下降法具体的迭代公式不再细说,相信大家都十分熟悉。我们经过足够次数的迭代,最终我们会确定对应的参数。
5.利用测试集对结果进行评估
前面的操作中,我们只是根据训练集的内容来按照我们的逻辑去找到所谓的最优解,但是这个最优解到底实不实用,还要看测试集的效果。当然,既然我们的目标就是预测,测试集当然本来就没有观测值,从而没办法查看效果;但是如果样本是随机的话,我们只要拿出一部分训练集的内容(理想状态当然是纯随机),不参与训练,并且用这些作为测试集,那我们就可以用这些数据的预测效果来评估我们的模型效果。以上方法如果分别取不同的训练集部分用来验证,也被称为交叉验证。
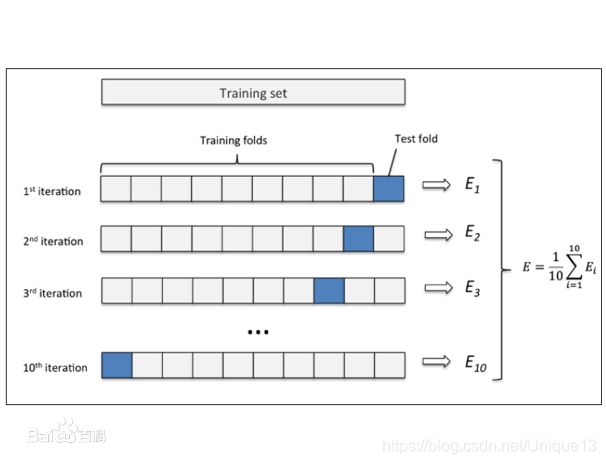
当然老师这里就是直接用的有标签的测试集,最终,训练好的线性模型的损失值是35.0。
6.重新选择函数模型,进入循环
就像在步骤二所说,对函数模型的选择是很多的(当然也可以增加新的特征等等),我们无法确定哪个更好,我们只能通过实际效果来选择相对最好的。老师这里没有加入新的特征,仅仅是选择了其他次数的多项式函数,得到以下结果。
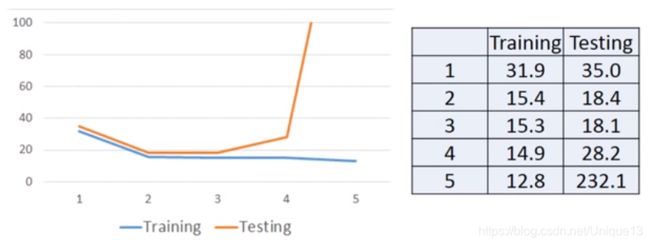
我们可以发现,随着拟合次数的增高,训练集上效果会变好(这是显然的),但测试集的效果反而变差了,这个现象我们就称之为过拟合。过拟合的原因和解决方式在下一节去详细介绍。