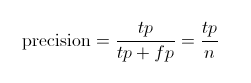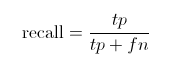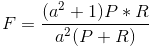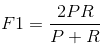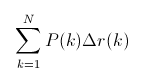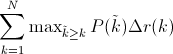【机器学习】查全率（Recall）/查准率（Precision）/F-Measure/AP（Average Precision）/MAP

感谢这篇博客：http://blog.csdn.net/hysteric314/article/details/54093734
最近也在看YOLO论文，这些基本问题一定要搞懂。

大雁与飞机

对一个二分问题来说，会出现四种情况。如果一个实例是正类并且也被预测成正类，即为真正类（True positive）,如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如果实例是负类被预测成负类，称之为真负类（True negative）,正类被预测成负类则为假负类（false negative）

之前看斯坦福机器学习课程，貌似用的是得肿瘤这件事来说明这个问题的，这里用到大雁与飞机也十分有趣。

现在做如下的定义：
True positives : 飞机的图片被正确的识别成了飞机。
True negatives: 大雁的图片没有被识别出来，系统判断正确。
False positives: 大雁的图片被错误地识别成了飞机。
False negatives: 飞机的图片没有被识别出来，系统判断错误。

也就是positives和negatives分别代表预测是正类还是负类，true和false分别代表你预测的正确性。

让我们对应一下下图看看是否理解了我们的假设：

那么在识别出的这四张照片中：
TP（True positives） : 有三个，画绿色框的飞机，飞机是正样本被成功预测了。
FP（False positives）: 有一个，画红色框的大雁，大雁是负样本，但是被检测出来所以错了。

没被识别出来的六张图片中：
TN（True negatives） : 有四个，这四个大雁的图片，系统判断正确不应该被检测出来。
FN（False negatives）: 有两个，两个飞机没有被识别出来，系统判断错误。

FP假正类，误检；FN假负类，负负得正应该是正样本，所以是漏检。

查准率（Precision）召回率（Recall）

可以计算一下上图的查准率召回率分别是多少。

Precision值应该是 3/（3+1）=0.75。
意味着在识别出的结果中，飞机的图片占75%。

Recall值是 3/（3+2）=0.6。
意味着在所有的飞机图片中，60%的飞机被正确的识别成飞机。

通俗点说Recall召回率也叫查全率，是宁可错杀一万不能放过一人，在搜索中意义重大，Precision在反垃圾邮件，疾病监测中应用比较多。但是这两个指标如何权衡一下呢？下面就引出了PR（Precision-Recall）曲线。

Precision-recall 曲线

如果你想评估一个分类器的性能，一个比较好的方法就是：观察当阈值变化时，Precision与Recall值的变化情况。如果一个分类器的性能比较好，那么它应该有如下的表现：Recall值增长的同时保持Precision的值在一个很高的水平。
根据调节阈值得出这样的数据：

画出如下曲线：

上图就是分类器的Precision-recall 曲线，在不损失精度的条件下它能达到40%Recall。而当Recall达到100%时，Precision 降低到50%。

P和R指标有的时候是矛盾的，那么有没有办法综合考虑他们呢？

综合评价指标（F-Measure）

最常见的方法应该就是F-Measure了，有些地方也叫做F-Score，其实都是一样的。

F-Measure是Precision和Recall加权调和平均：

当参数a=1时，就是最常见的F1了：

很容易理解，F1综合了P和R的结果，当F1较高时则比较说明实验方法比较理想。

AP（Average Precision ）

Approximated Average precision:

相比较与曲线图，在某些时候还是一个具体的数值能更直观地表现出分类器的性能。通常情况下都是用 Average Precision来作为这一度量标准，它的公式为：

在这一积分中，其中p代表Precision ，r代表Recall，p是一个以r为参数的函数，相当于求曲线下面积。

实际上这一积分极其接近于这一数值：对每一种阈值分别求（Precision值）乘以（Recall值的变化情况），再把所有阈值下求得的乘积值进行累加，更加方便了我们的计算，公式如下：

在这一公式中，N代表测试集中所有图片的个数，P(k)表示在能识别出k个图片的时候Precision的值，而 Delta r(k) 则表示识别图片个数从k-1变化到k时（通过调整阈值）Recall值的变化情况。

在这一例子中，Approximated Average Precision的值
=(1 * （0.2-0）) + (1 * (0.4-0.2)) + (0.66 * (0.4-0.4)) + (0.75 * (0.6-0.4)) + (0.6 * (0.6-0.6)) + (0.66 * (0.8-0.6)) + (0.57 * (0.8-0.8)) + (0.5 * (0.8-0.8)) + (0.44 * (0.8-0.8)) + (0.5 * (1-0.8)) = 0.782.

=(1 * 0.2) + (1 * 0.2) + (0.66 * 0) + (0.75 * 0.2) + (0.6 * 0) + (0.66 * 0.2) + (0.57 * 0) + (0.5 * 0) + (0.44 * 0) + (0.5 * 0.2) = 0.782.

通过计算可以看到，那些Recall值没有变化的地方（加粗部分），对增加Average Precision值没有贡献。

Interpolated average precision:

不同于Approximated Average Precision，一些作者选择另一种度量性能的标准：Interpolated Average Precision。公式如下：

也就是也就是每次使用在所有阈值的Precision中，最大值的那个Precision值与Recall的变化值相乘。

这张图看起来容易理解一点，但是图片中使用的参数与上面所说的例子无关。

很明显 Approximated Average Precision与精度曲线挨的很近，而使用Interpolated Average Precision算出的Average Precision值明显要比Approximated Average Precision的方法算出的要高。

一些很重要的文章都是用Interpolated Average Precision 作为度量方法，并且直接称算出的值为Average Precision 。PASCAL Visual Objects Challenge从2007年开始就是用这一度量制度，他们认为这一方法能有效地减少Precision-recall 曲线中的抖动。所以在比较文章中Average Precision 值的时候，最好先弄清楚它们使用的是那种度量方式。

MAP（Mean Average Precision）

平均正确率的值，对于分许多类的情况适用，例如YOLO，所以它只是在AP基础上求了平均，把每个类的AP求和再平均。

好啦～希望这篇博客对你有用，有错误欢迎指正！

参考：
http://blog.csdn.net/hysteric314/article/details/54093734
https://sanchom.wordpress.com/tag/average-precision/