Self-attention构建的原因:从直觉出发
文章目录
-
- 一、RNN与CNN的不足
-
- 1. RNN
- 2. CNN
- 二、attention提出的原因
-
- 1. 想要并行计算的同时考虑整个sentence
- 2. $\alpha$如何得到
- 3. 合起来看一下(小总结)
- 三、终极总结
先写点无用的:之前大学光玩了,没有好好学习,毕了业才发现自己一无是处。过去的就不提了,从现在开始认真学习,以AI大师为目标,像神奇宝贝中的小智一样争取成为一名优秀的AI训练师。
之前没有写博客的习惯,是因为从来没有自己认真思索。但在AI这个方兴未艾的行业,大量学习完之后再总结思考这两项缺一不可。OK,那就从今儿起记录一下,成为AI训练师路上所打过得那些关卡。一方面,给未来的自己留下资料方便回忆;一方面,给未来的自己留下一笔精神财富;一方面,也给其他同行提供一个思考问题的角度。
OK,下面进入正题。现在在学NLP,学到了现在最主流的模型BERT。BERT用了不同于CNN,RNN的核心hidden layer就是self attention。那么为什么google的大佬会创造出这种神奇的layer呢,我从自己的直觉出发,试图还原大佬们创造的初衷。 想偷懒的,或者中间有看不太懂得话,建议直接看总结!!!直接看总结!!!直接看总结!!!
深推李宏毅老师的attention课程:https://www.youtube.com/watch?v=ugWDIIOHtPA&list=PLJV_el3uVTsOK_ZK5L0Iv_EQoL1JefRL4&index=61
然后转载我的blog的话可以请大家链接上原博客的地址吗:https://blog.csdn.net/Skywalker1111/article/details/115461167
一、RNN与CNN的不足
很简单,熟悉NLP的应该都知道,在language model中吃(input)吐(output)的都是sequence,也就是seq2seq model,也就是一个个向量的连续序列。那么,在train的过程中,怎么能够让模型在吃一个token的同时考虑其上下文的information,非常重要。就像money from bank 和river bank同样的word,但是因为hidden layer能考虑bank的上下文,所以把两个bank分成了两个不同的tokens(它们是同一个word,确是两个tokens)。
1. RNN
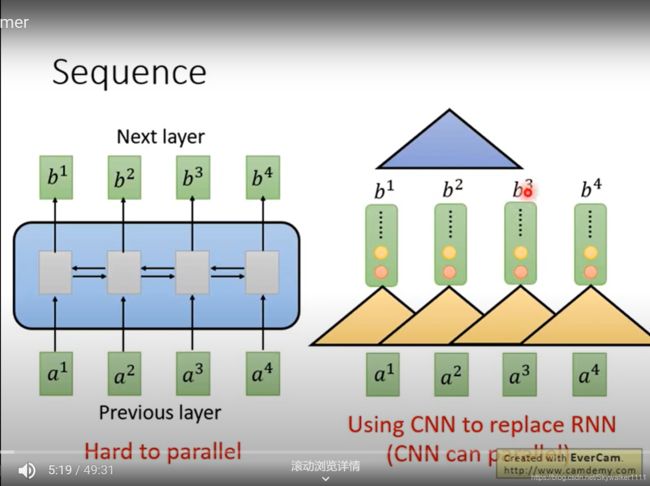
因此,吃一句话中的每一个vector作为输入的同时,最好需要考虑到整个sentence的所有其他单词。RNN就应运而生了。RNN模型不多赘述,优点是可以通过历史记录的方式,考虑整句话的所有语义。缺点是必须先吃第一个单词x1,吐出第一个y1然后才能再吃第二个vector x2,因此其不能并行,也就是其训练的时间会非常之长。(现在说的RNN都是LSTM,RNN已经没有只用naive RNN的了)
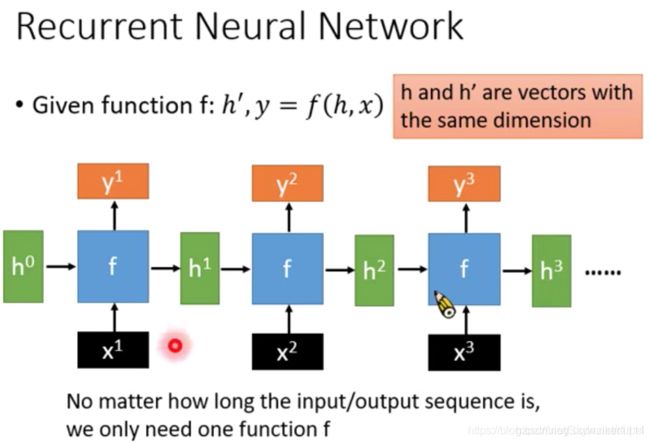
2. CNN
有人说为了并行,可以用CNN,的确,CNN可以并行计算,也因为其感受野可以一次感受filter size个input。但是,CNN却不能一次感受整句话(如果想要感受更多的input,那么需要更深层的CNN,也就是叠罗汉)。因此,无论CNN还是RNN都不是最优的选择。
二、attention提出的原因
重点来了 重点来了 重点来了 重要的话说三遍。
这里我用自顶向下的方法,带着问题从intuition出发还原attention的构造之旅,因此照片与李宏毅老师讲课的ppt顺序正好相反。
1. 想要并行计算的同时考虑整个sentence
怎么才能做到这个看似很难却又实则简单的需求呢?如果局限在RNN,CNN里面是不可能完成的。因此attention抛弃了这两个久负盛名网络的核心layer,跳出了思维定势。
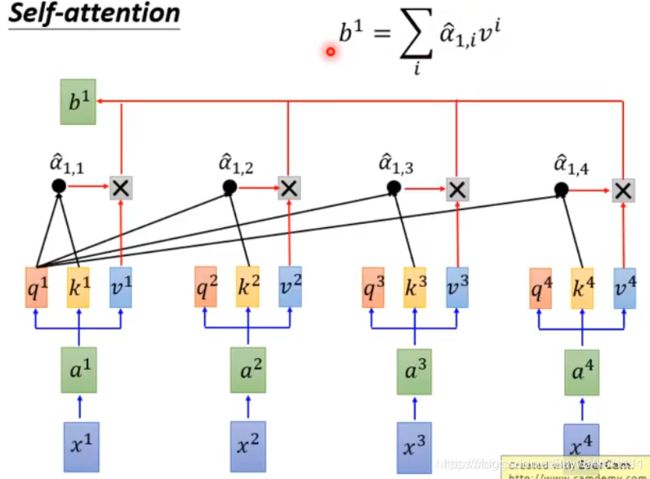
大道至简,其实直接 y j = α 1 x 1 + α 2 x 2 + . . . + α n x n y_j=\alpha_1x_1+\alpha_2x_2+...+\alpha_nx_n yj=α1x1+α2x2+...+αnxn(j是指输出位置)就好了,也就是weighted sum,也就是 y j = ∑ i α i x i y_j=\sum_{i}\alpha_ix_i yj=∑iαixi,这个式子其实跟下图的 b 1 = ∑ b^1=\sum b1=∑那一串是一样的。这里,要注意的有两点。1. ∑ i α i = 1 \sum_{i}\alpha_i=1 ∑iαi=1, α \alpha α就是权重,那么权重之和理应是1(怎么让和不是1的一堆 α \alpha α变成和是1?做softmax啊!下面我们就会看到!!!) 2. 一般来说,计算 y 1 y_1 y1的时候 α 1 \alpha_1 α1理应更大一点,也就是说输出y1主要考虑的是输入x1,顺便考虑其他的x,但其他的x都应该没有x1的权重大。
这个步骤就叫做attention,也就是专注,因为这个输出y可以专注在几个特殊的 α \alpha α中,不想要的让 α = 0 \alpha=0 α=0就好了
2. α \alpha α如何得到
y = ∑ i α i x i y=\sum_{i}\alpha_ix_i y=∑iαixi,也就是说输出是输入的weighted sum。x已经有了,那么weights: α \alpha α是怎么得到的呢?众所周知,每个 α \alpha α都是常量,是一个数字,如果人为设定显然不合适。我们希望的是, α \alpha α能在对应的x时变大,在其他x时稍小一些,这样既着重考虑到了当前输入,也考虑全了整句话(有主有辅)。也就是上面提到的注意两点中的第二点。因此,这个 α \alpha α最好能够根据自己的输入x动态调节。这是第一层。
然而细思一下, α \alpha α只跟当前的输入x有关么?当然不是!这个权重 α \alpha α不仅需要考虑当前输入x,也要考虑到当前输入与其他每一个输入的corelation。这是符合直觉的。比如我们说做机器翻译训练:I am Sam的时候,当前输入"I",希望的输出是“我”,这个我考虑I的权重最大,考虑am的权重次之,考虑Sam的权重最少。因为,I与am的corelation要更密切。因此,第二层就是, α \alpha α最好应该考虑到两个因素,当前的输入外加此 α \alpha α对应的输入。就比如说 y 1 = α 1 x 1 + α 2 x 2 + . . . + α n x n y_1=\alpha_1x_1+\alpha_2x_2+...+\alpha_nx_n y1=α1x1+α2x2+...+αnxn,那么当前输入时x1,输出是y1,那么 α 2 \alpha_2 α2就应该考虑输入x1与当前 α 2 \alpha_2 α2作用的x2, α 3 \alpha_3 α3就应该考虑输入x1与 α 3 \alpha_3 α3作用的x3。
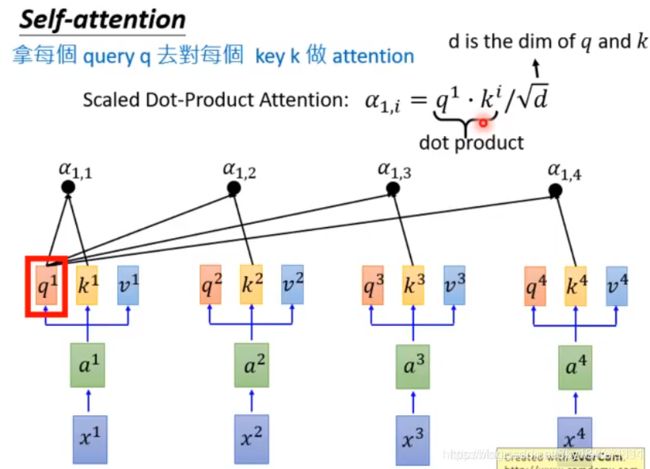
最后,我们就应该站在第五层(甚至是大气层)进行总结:1. α \alpha α不要固定,但它还是一个常量数字 2.每个 α \alpha α能够根据两个input动态变化。快快快!怎么样从两个向量得到一个常数? 当然是两个vector做inner product!比如当前的输出是 y j y_j yj,那么 α j , i = x j ⋅ x i \alpha_{j,i}=x_j\cdot x_i αj,i=xj⋅xi其中j是指当前输出位置是j,i是说 α \alpha α权重将要作用的的向量是i。这个 α \alpha α就是j与i的corelation通过inner product得到的。它其实就是下面图片的Scaled Dot-Product Attention公式的主题。只不过除以根号d是因为要根据输入的dimension做scaled修正。(为啥是除以根号d,不是除以d,不是除以d平方,这个李老师也没提)
3. 合起来看一下(小总结)
我们有了 y j = ∑ i α i x i y_j=\sum_{i}\alpha_ix_i yj=∑iαixi,我们有了 α j , i = x j ⋅ x i \alpha_{j,i}=x_j\cdot x_i αj,i=xj⋅xi,把它两个合并, y j = ∑ i ( x j ⋅ x i ) x i y_j=\sum_{i}(x_j\cdot x_i)x_i yj=∑i(xj⋅xi)xi,注意, ( x j ⋅ x i ) (x_j\cdot x_i) (xj⋅xi)是一个常数数字,且取值(0,1)(因为这里其实对所有的 α \alpha α做了softmax)。举个例子,在做机翻,I am Sam,希望输入的y1就是“我”,那么 y 1 = ( x 1 ⋅ x 1 ) x 1 + ( x 1 ⋅ x 2 ) x 2 + ( x 1 ⋅ x 3 ) x 3 y_1=(x_1\cdot x_1)x_1+(x_1\cdot x_2)x_2+(x_1\cdot x_3)x_3 y1=(x1⋅x1)x1+(x1⋅x2)x2+(x1⋅x3)x3。注意到,我们每一个部分 ( x j ⋅ x i ) x i (x_j\cdot x_i)x_i (xj⋅xi)xi都需要吃三次向量(虽然此时 x i x_i xi用了两遍,但是总的也是一共要用三次向量)
Perfect!!! 这就是attention layer的骨干,我们再在骨干上给它添一点血肉,稍微包装一下。也就是每一个input x i x_i xi都给他乘一个矩阵,对它进行一下线性变化。因为需要吃三次向量,我们就拿出三个矩阵W做变换,这三个W都需要来学习。上面的 y j = ∑ i ( x j ⋅ x i ) x i y_j=\sum_{i}(x_j\cdot x_i)x_i yj=∑i(xj⋅xi)xi就变成了 y j = ∑ i ( W q x j ⋅ W k x i ) W v x i y_j=\sum_{i}(W^qx_j\cdot W^kx_i)W^vx_i yj=∑i(Wqxj⋅Wkxi)Wvxi。如下图所示, W q x j = q j W^qx_j=q^j Wqxj=qj被叫做了query, W k x i = k i W^kx_i=k^i Wkxi=ki被叫做key, W v x i = v i W^vx_i=v^i Wvxi=vi被叫做value。
那么有人说,李老师ppt写的是a,你怎么写的是x。害,为了再更加丰满一下这个模型,x再乘一个待学习的矩阵W不就变成了a么, a i = W x i a^i=Wx^i ai=Wxi。
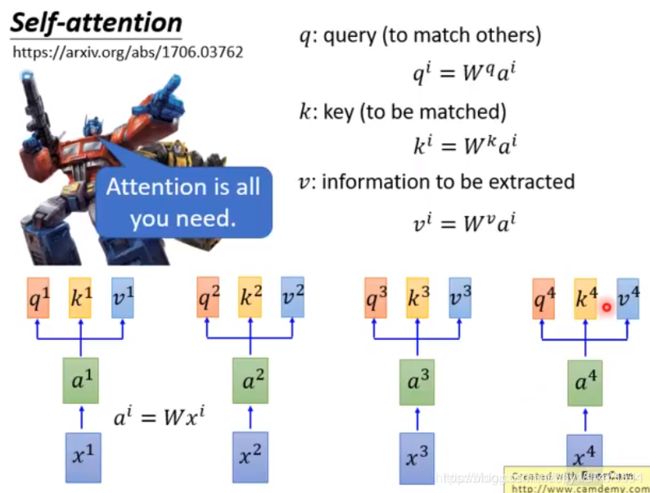
三、终极总结
自上而下:
- 需要考虑整句话的information,因此引入 α \alpha α作为weight作用于整句话所有的input vector。
- 需要 α \alpha α考虑当前输入的同时也考虑考虑到其作用的vector,因此将这两个input做inner product得到两个向量的corelation。
- 得到的 α \alpha α乘以相应的input x,做weighted sum就可以得到输出y
- 最后进行几层包装,乘上一些线性变化的矩阵即可。
自下而上:
- 每一个输入都先乘矩阵W做变换得到a
- 每一个a都要乘三个W( W q W^q Wq W k W^k Wk W v W^v Wv)衍生变化出三个向量q,k,v。
- 当前输出为 y j y^j yj的情况下,用第j个位置的 q j q^j qj去match所有其他的 k i k^i ki,这样就得到了 α i \alpha ^i αi,记得要把 α i \alpha ^i αi做一下softmax,使得 ∑ i α i = 1 \sum_{i}\alpha ^i=1 ∑iαi=1
- 得到的 α i \alpha ^i αi乘以 v i v ^i vi就是当前向量将被参考的最终形式,求weighted sum就把一整句话所有所有向量都进行综合参考。