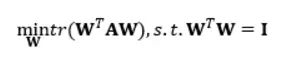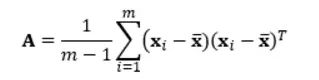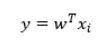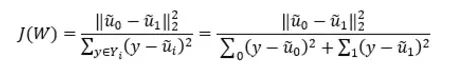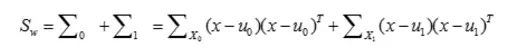当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。

7.5.1 主成分分析法（PCA）

1 PCA原理

Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。
　　通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是PCA并不试图去探索数据内在结构）。
设n维向量w为目标子空间的一个坐标轴方向（称为映射向量），最大化数据映射后的方差，有：

最大化数据映射后的方差

其中m是数据实例的个数， x_i 是数据实例i的向量表达是所有数据实例的平均向量。定义w 为包含所有映射向量为列向量的矩阵，经过线性代数变换，可以得到如下优化目标函数：

优化目标函数

其中tr表示矩阵的迹。

协方差矩阵

A是数据协方差矩阵。
　　容易得到最优的W是由数据协方差矩阵前k个最大的特征值对应的特征向量作为列向量构成的。这些特征向量形成一组正交基并且最好地保留了数据中的信息。
　　PCA的输出就是Y = W‘X，由X的原始维度降低到了k维。
　　PCA追求的是在降维之后能够最大化保持数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据的区分作用并不大，反而可能使得数据点揉杂在一起无法区分。这也是PCA存在的最大一个问题，这导致使用PCA在很多情况下的分类效果并不好。具体可以看下图所示，若使用PCA将数据点投影至一维空间上时，PCA会选择2轴，这使得原本很容易区分的两簇点被揉杂在一起变得无法区分；而这时若选择1轴将会得到很好的区分结果。

2. PCA代码实现

使用decomposition库的PCA类选择特征的代码如下：

from sklearn.decomposition import PCA
#主成分分析法，返回降维后的数据
#参数n_components为主成分数目
PCA(n_components=2).fit_transform(iris.data)

7.5.2 线性判别分析法（LDA）

1. LDA原理

使用Linear Discriminant Analysis (也有叫做Fisher Linear Discriminant)是一种有监督的（supervised）线性降维算法。与PCA保持数据信息不同，LDA是为了使得降维后的数据点尽可能地容易被区分。
　　假设原始数据表示为X，（m*n矩阵，m是维度，n是sample的数量），既然是线性的，那么就是希望找到映射向量a，使得 a’X后的数据点能够保持以下两种性质：
1.同类的数据点尽可能的接近（within class）

不同类的数据点尽可能的分开（between class）
　　举一个直观的例子，如下图：红色和蓝色点代表数据分别属于两个不同类，与PAC最大化保持数据信息的思想不同，LDA会这样降维这两堆点：

可以看到，虽然降维之后数据更加聚集了，但是更好区分了。
　　一般地，设有数据集D,投影向量为w，则点x_i经过投影后为：

投影后的x_i

投影前的样本中心点为u，投影后的中心点为：

投影后的中心点

我们希望投影后不同类别的样本尽量离得较远，使用度量值：

所以总的优化目标函数为：

优化目标函数

J(W)自然是越大越好。
　　定义类内散度矩阵为：

类内散度矩阵

定义类间散度矩阵：

类间散度矩阵

所以

因为向量w的长度成比例改变不影响J的取值，所以我们令w^TS_ww=1，那么原优化目标就变为

使用拉格朗日乘子法,解得：

进一步解得：

2. LDA代码实现

使用lda库的LDA类选择特征的代码如下：

from sklearn.lda import LDA 
#线性判别分析法，返回降维后的数据
#参数n_components为降维后的维数
LDA(n_components=2).fit_transform(iris.data, iris.target)

7.5.3 PCA与LDA的对比

PCA与LDA降维的对比：

　　PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。
　　PCA技术的一个很大优点在于，它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。
　　LDA以标签类别衡量差异性的有监督降维方式，相对于PCA的模糊性，其目的更明确，更能反映样本间的差异。缺点在于局限性大，受样本种类限制，且至多可生成C-1维子空间（C为类别数量），也就是说LDA降维后的维度空间在[1，C-1],与原始特征无关。因此，对于二分类问题，最多投影到1维。另外，LDA不适合对非高斯分布样本进行降维。

7.5 数据降维