MATLAB的线性规划工具

MATLAB的线性规划工具

问题描述

某次考试，总分100分.分三种题型：

单选题13题，每题3分，共39分.
多选题10题，每题3.1分，共31分.
判断题12题，每题2.5分，共30分.

交卷之后，只知道分数为79.3，问：单选题、多选题、判断题分别做错了多少？

MATLAB meshz辅助求解

假设单选题、多选题、判断题做错数量分别为x,y,z.则可列方程：
$$3x+3.1y+2.5z=100-79.3$$
$$3x+3.1y+2.5z=20.7$$

上述函数是一个空间平面，如果不理解为什么是空间平面可以参考直线与平面方程的几何表达.

最直接的办法就是把平面绘制出来，找到上面的正整数解，脚本如下：

s = linspace(0, 10, 11);
t = linspace(0, 10, 11);
[ss, tt] = meshgrid (s, t);
x = tt;
y = ss;
z = -(3.*x + 3.1.*y  - 20.70)/2.5;
pbaspect ([1 1 1]);

meshz(x, y, z);

patch([0 10 10 0], [0 0 10 10], [0 0 0 0]) 

camproj('perspective')
xlabel('x');
ylabel('y');
set( gca, 'ydir', 'reverse' )

对应图像：

绿色平面之上的部分就是要搜索的区域.
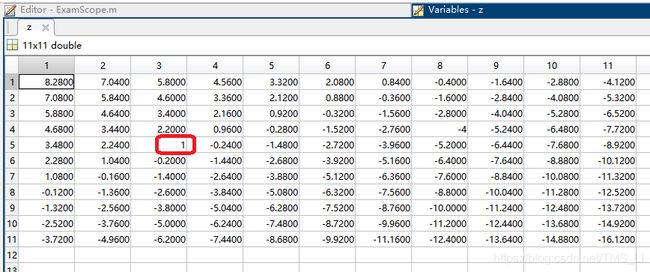
脚本中x，y变量使用的都是正整数，所以只要确保z也是正整数就可以了，可以查看z的数值：

显然z只能取1，对应的x,y分别为4与2，所以这个问题的解是: $x=4,y=2,z=1$

MATLAB intlinprog函数求解

显然，上述的方法很难让人满意，因为这个解是靠肉眼观察出来的.
实事上MATLAB有专门函数求解，就是intlinprog().

上述问题可以写成下列条件：

$x_1,x_2,x_3$为整数

$x_1\ge 0$

$x_2\ge 0$

$x_3\ge 0$

$3x_1+3.1x_2+2.5x_3=20.7$

求$3x_1+3.1x_2+2.5x_3$的最小值.

编制脚本：

Aeq = [3,3.1,2.5];
beq = 20.7;
intcon = 1:3;
f = [3;3.1;2.5];

A = [
    -1,0,0;
    0,-1,0;
    0,0,-1;
    ];

b = [0;0;0];

x = intlinprog(f,intcon,A,b,Aeq,beq)

常见线性规划问题

甲乙两种溶液，要兑成另一个产品.
但有成本限制,不成超过15，甲的单价是3，乙的是5.
甲乙都含有害成分，对它浓度的要求不能超过2%，对于此成分，甲的浓度为5%，乙的浓度为1%.
现在想把这个产品尽可能地做重，问应该分别使用多少的甲与乙？

直观的观察是，要花更少的钱，做去更多的产品，只能尽量使用便宜的甲，但甲的有害成分又比较高，一味的选用甲也不行，这是问题所在.

这是一个典型的线性规划问题.假设甲乙两种溶液的质量分别是x,y,可以列出下面的约束不等式：

$3x+5y\le 15(1)$

$(0.05x+0.01y)/(x+y)<0.02$

化简后：

$3x-y\le 0(2)$

所求为令目标函数x+y最大.

两个不等式边界直线为AB与CG，目标函数直线与EF平行：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NXJCTdwC-1619772875284)(./geogebra-export.png )]

显然G是所求的点，
求解线性方程得AB与CG交点为，$(\frac{5}{6},\frac{5}{2})$
最大值为$\frac{10}{3}$

linprog求解

编制脚本：

A = [
    3,5;
    3,-1;
    ];
b = [15;0];
f = [-1;-1];
x = linprog(f,A,b)

结果与手工计算相同.

参考

• 直线与平面方程的几何表达
• https://www.mathworks.com/help/optim/ug/linprog.html
• https://www.mathworks.com/help/optim/ug/intlinprog.html