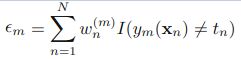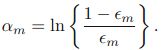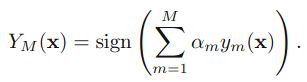机器学习实践之集成方法(随机森林和AdaBoost元算法提高分类性能)
本文根据最近学习机器学习书籍网络文章的情况,特将一些学习思路做了归纳整理,详情如下.如有不当之处,请各位大拿多多指点,在此谢过。
(未添加文章标签,特此补上,2018.1.14记。)
一、概述
1、概念理解
集成学习方法是指组合多个模型,以获得更好的效果,使集成的模型具有更强的泛化能力。对于多个模型,如何组合这些模型,主要有以下几种不同的方法
- 在验证数据集上上找到表现最好的模型作为最终的预测模型;
- 对多个模型的预测结果进行投票或者取平均值;
- 对多个模型的预测结果做加权平均。
集成学习在机器学习算法中具有较高的准去率,不足之处就是模型的训练过程可能比较复杂,效率不是很高。目前接触较多的集成学习主要有2种:基于Boosting的和基于Bagging,前者的代表算法有Adaboost、GBDT、XGBOOST、后者的代表算法主要是随机森林。
2、主要思想
通俗地来说,当一个项目做出重大决定时,当事人可能会考虑吸取多个专家而不是一个专家的意见,同理,机器学习也是一样的做法。
书面语言:集成学习的主要思想是利用一定的手段学习出多个分类器,而且这多个分类器要求是弱分类器,然后将多个分类器进行组合公共预测。核心思想就是如何训练处多个弱分类器以及如何将这些弱分类器进行组合。
3、集成方法
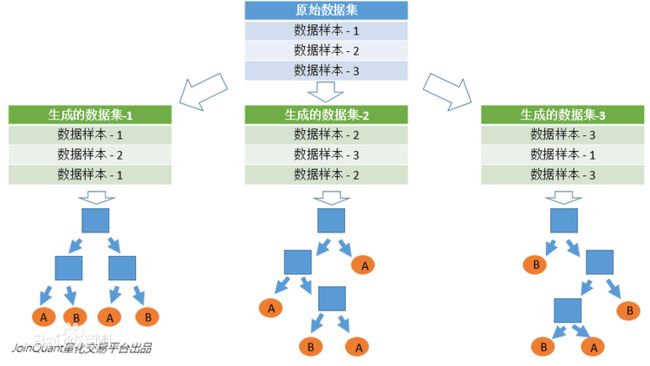
- 随机森林(Random Forest: bagging + 决策树):将训练集按照横(随机抽样本)、列(随机抽特征)进行有放回的随机抽取,获得n个新的训练集,训练出n个决策树,通过这n个树投票决定分类结果。主要的parameters 有n_estimators 和 max_features。民间有个说法,三个臭皮匠顶个诸葛亮,这里的随机森林就是希望多构建几个臭皮匠,以期最后的模型分类效果能够超过单个诸葛亮的算法。
- Adaboost (adaptive boosting: boosting + 单层决策树):训练数据中的每个样本,并赋予其一个权重,这些权重构成了向量D。一开始,这些权重都初始化成相等值。首先在训练数据上训练出一个弱分类器并计算该分类器的错误率,然后在统一数据集上再训练分类器。在第二次训练中,会调高那些前一个分类器分类错误的样本的权重。如此反复,训练出许多分类器来进行加权投票,每个分类器的权重是基于该分类器的错误率计算出来的。
二、集成方法场景
1、投票选举(bagging: 自举汇聚法 bootstrap aggregating)
是基于数据随机重抽样分类器构造的方法。以bagging方法最流行的版本--随机森林(random forest)为例:
一个美女正在选择男友,她让自己的10个闺蜜都给出每个男生的综合评分,最终选择了一个综合评分最高的男生作为自己的男友。
2、再学习(boosting)
是基于所有分类器的加权求和的方法。 以boosting方法最流行的版本--AdaBoost算法为例:
四个帅哥追同一个美女
第一个帅哥失败-->(传授经验:姓名、身高、五官、皮肤、家庭);第二个帅哥失败-->(传授经验: 兴趣爱好、日常习惯、性格特点);第三个帅哥失败-->(传授经验:择偶要求、未来规划、理想生活方式);第四个帅哥成功。
3、bagging和boost的区别
- bagging 是一种与 boosting 很类似的技术, 所使用的多个分类器的类型(数据量和特征量)都是一致的。
- bagging 是由不同的分类器(1.数据随机化 2.特征随机化)经过训练,综合得出的出现最多分类结果;boosting 是通过调整已有分类器错分的那些数据来获得新的分类器,得出目前最优的结果。
- bagging 中的分类器权重是相等的;而 boosting 中的分类器加权求和,所以权重并不相等,每个权重代表的是其对应分类器在上一轮迭代中的成功度。
三、随机森林
随机森林的构建有两个方面:样本的随机化、待分类特征的随机化。使得随机森林中的决策都彼此不同,增加系统的多样性,以此提升分类的性能。
1、数据(样本)的随机化
使得随机森林中的决策更加普遍化一些,以便适合更多的场景。一般情况下,有放回的准确率在70%以上,无放回的准确率在60%以上。
- 采用有放回的抽样方式,构建多个子数据集,保证各个子集之间拥有相同的数量级(不同子集、同一子集之间的元素可以重复使用);
- 利用子数据集构建子决策树,将该数据放入每个子决策树之中,每个子决策树输出一个结果;
- 然后,统计子决策树的投票结果,得到最终的分类,即随机森林的输出结果;
- 如下图,假设随机森林中有3棵子决策树,2棵子树的分类结果是A类,1棵子树的分类结果是B类,那么随机森林的分类结果就是A类。
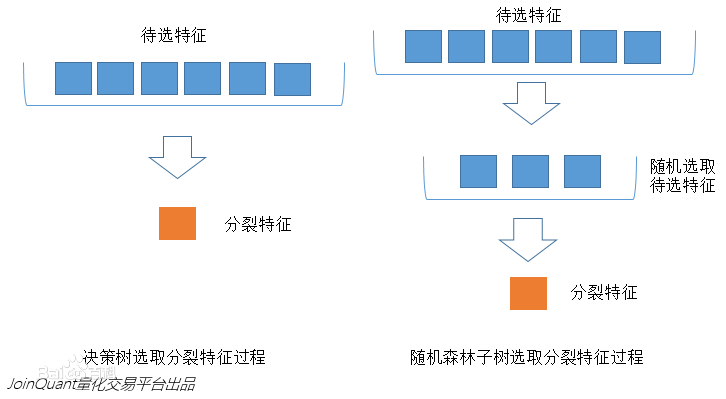
2、待选特征的随机化
- 子树从所有的待选特征中随机选取一定的特征;
- 在选取的特征中选择最优特征。
下图中,蓝色的方块代表所有可以被选择的特征,也就是目前的待选特征;黄色的方块是分裂特征。
左边是一棵决策树的特征选取过程,通过在待选特征中选取最优的分裂特征(别忘了前文提到的ID3算法,C4.5算法,CART算法等等),完成分裂。
右边是一个随机森林中的子树的特征选取过程。
3、随机森林开发的流程
- 收集数据:任何方法;
- 准备数据: 转换样本集;
- 分析数据: 任何方法;
- 训练算法: 通过数据随机化和特征随机化,进行多实例的分类评估;
- 测试算法: 计算错误率;
- 使用算法: 输入样本数据,通过随机森林算法判断数据的分类属于哪个分类,对计算出的分类结果进行后续处理。
4、随机森林算法的特点
- 优点: 几乎不需要进行输入准备、可实现隐式特征选择、训练速度非常快、其他模型难以超越,很难建立一个糟糕的随机森林算法模型,大量免费开源的实现路径。
- 缺点: 劣势在于模型大小,是很难去解释的黑盒子。
- 适用数据特征: 数值型和标称型。
四、项目案例--声呐信号分类
1、项目概述
采用 Gorman 和 Sejnowski 在研究使用神经网络的声纳信号分类中使用的数据集(sonar-all-data.txt),目标是使用训练算法得到一个模型以便区分声呐信号。
2、开发流程
- 收集数据: 提供的样本数据集。
- 准备数据: 转换样本集。
- 分析数据: 人工检查数据。
- 训练算法: 在数据上,使用random_forest()函数进行优化评估,返回模型的综合分类结果。
- 测试算法: 在使用自定义n_folds份随机重抽样,进行测试评估,获取综合的预测得分情况。
- 使用算法: 构建完整的应用程序,进行测试集预测分类。
3、样本数据集样式
收集数据: 提供的样本数据集
0.0286 0.0453 0.0277 0.0174 0.0384 0.099 0.1201 0.1833 0.2105 0.3039 0.2988 0.425 0.6343 0.8198 1 0.9988 0.9508 0.9025 0.7234 0.5122 0.2074 0.3985 0.589 0.2872 0.2043 0.5782 0.5389 0.375 0.3411 0.5067 0.558 0.4778 0.3299 0.2198 0.1407 0.2856 0.3807 0.4158 0.4054 0.3296 0.2707 0.265 0.0723 0.1238 0.1192 0.1089 0.0623 0.0494 0.0264 0.0081 0.0104 0.0045 0.0014 0.0038 0.0013 0.0089 0.0057 0.0027 0.0051 0.0062 R
0.0317 0.0956 0.1321 0.1408 0.1674 0.171 0.0731 0.1401 0.2083 0.3513 0.1786 0.0658 0.0513 0.3752 0.5419 0.544 0.515 0.4262 0.2024 0.4233 0.7723 0.9735 0.939 0.5559 0.5268 0.6826 0.5713 0.5429 0.2177 0.2149 0.5811 0.6323 0.2965 0.1873 0.2969 0.5163 0.6153 0.4283 0.5479 0.6133 0.5017 0.2377 0.1957 0.1749 0.1304 0.0597 0.1124 0.1047 0.0507 0.0159 0.0195 0.0201 0.0248 0.0131 0.007 0.0138 0.0092 0.0143 0.0036 0.0103 R
0.0519 0.0548 0.0842 0.0319 0.1158 0.0922 0.1027 0.0613 0.1465 0.2838 0.2802 0.3086 0.2657 0.3801 0.5626 0.4376 0.2617 0.1199 0.6676 0.9402 0.7832 0.5352 0.6809 0.9174 0.7613 0.822 0.8872 0.6091 0.2967 0.1103 0.1318 0.0624 0.099 0.4006 0.3666 0.105 0.1915 0.393 0.4288 0.2546 0.1151 0.2196 0.1879 0.1437 0.2146 0.236 0.1125 0.0254 0.0285 0.0178 0.0052 0.0081 0.012 0.0045 0.0121 0.0097 0.0085 0.0047 0.0048 0.0053 R
0.0223 0.0375 0.0484 0.0475 0.0647 0.0591 0.0753 0.0098 0.0684 0.1487 0.1156 0.1654 0.3833 0.3598 0.1713 0.1136 0.0349 0.3796 0.7401 0.9925 0.9802 0.889 0.6712 0.4286 0.3374 0.7366 0.9611 0.7353 0.4856 0.1594 0.3007 0.4096 0.317 0.3305 0.3408 0.2186 0.2463 0.2726 0.168 0.2792 0.2558 0.174 0.2121 0.1099 0.0985 0.1271 0.1459 0.1164 0.0777 0.0439 0.0061 0.0145 0.0128 0.0145 0.0058 0.0049 0.0065 0.0093 0.0059 0.0022 R
0.0164 0.0173 0.0347 0.007 0.0187 0.0671 0.1056 0.0697 0.0962 0.0251 0.0801 0.1056 0.1266 0.089 0.0198 0.1133 0.2826 0.3234 0.3238 0.4333 0.6068 0.7652 0.9203 0.9719 0.9207 0.7545 0.8289 0.8907 0.7309 0.6896 0.5829 0.4935 0.3101 0.0306 0.0244 0.1108 0.1594 0.1371 0.0696 0.0452 0.062 0.1421 0.1597 0.1384 0.0372 0.0688 0.0867 0.0513 0.0092 0.0198 0.0118 0.009 0.0223 0.0179 0.0084 0.0068 0.0032 0.0035 0.0056 0.004 R
0.0039 0.0063 0.0152 0.0336 0.031 0.0284 0.0396 0.0272 0.0323 0.0452 0.0492 0.0996 0.1424 0.1194 0.0628 0.0907 0.1177 0.1429 0.1223 0.1104 0.1847 0.3715 0.4382 0.5707 0.6654 0.7476 0.7654 0.8555 0.972 0.9221 0.7502 0.7209 0.7757 0.6055 0.5021 0.4499 0.3947 0.4281 0.4427 0.3749 0.1972 0.0511 0.0793 0.1269 0.1533 0.069 0.0402 0.0534 0.0228 0.0073 0.0062 0.0062 0.012 0.0052 0.0056 0.0093 0.0042 0.0003 0.0053 0.0036 R
0.0123 0.0309 0.0169 0.0313 0.0358 0.0102 0.0182 0.0579 0.1122 0.0835 0.0548 0.0847 0.2026 0.2557 0.187 0.2032 0.1463 0.2849 0.5824 0.7728 0.7852 0.8515 0.5312 0.3653 0.5973 0.8275 1 0.8673 0.6301 0.4591 0.394 0.2576 0.2817 0.2641 0.2757 0.2698 0.3994 0.4576 0.394 0.2522 0.1782 0.1354 0.0516 0.0337 0.0894 0.0861 0.0872 0.0445 0.0134 0.0217 0.0188 0.0133 0.0265 0.0224 0.0074 0.0118 0.0026 0.0092 0.0009 0.0044 R
0.0079 0.0086 0.0055 0.025 0.0344 0.0546 0.0528 0.0958 0.1009 0.124 0.1097 0.1215 0.1874 0.3383 0.3227 0.2723 0.3943 0.6432 0.7271 0.8673 0.9674 0.9847 0.948 0.8036 0.6833 0.5136 0.309 0.0832 0.4019 0.2344 0.1905 0.1235 0.1717 0.2351 0.2489 0.3649 0.3382 0.1589 0.0989 0.1089 0.1043 0.0839 0.1391 0.0819 0.0678 0.0663 0.1202 0.0692 0.0152 0.0266 0.0174 0.0176 0.0127 0.0088 0.0098 0.0019 0.0059 0.0058 0.0059 0.0032 R
0.009 0.0062 0.0253 0.0489 0.1197 0.1589 0.1392 0.0987 0.0955 0.1895 0.1896 0.2547 0.4073 0.2988 0.2901 0.5326 0.4022 0.1571 0.3024 0.3907 0.3542 0.4438 0.6414 0.4601 0.6009 0.869 0.8345 0.7669 0.5081 0.462 0.538 0.5375 0.3844 0.3601 0.7402 0.7761 0.3858 0.0667 0.3684 0.6114 0.351 0.2312 0.2195 0.3051 0.1937 0.157 0.0479 0.0538 0.0146 0.0068 0.0187 0.0059 0.0095 0.0194 0.008 0.0152 0.0158 0.0053 0.0189 0.0102 R
0.0124 0.0433 0.0604 0.0449 0.0597 0.0355 0.0531 0.0343 0.1052 0.212 0.164 0.1901 0.3026 0.2019 0.0592 0.239 0.3657 0.3809 0.5929 0.6299 0.5801 0.4574 0.4449 0.3691 0.6446 0.894 0.8978 0.498 0.3333 0.235 0.1553 0.3666 0.434 0.3082 0.3024 0.4109 0.5501 0.4129 0.5499 0.5018 0.3132 0.2802 0.2351 0.2298 0.1155 0.0724 0.0621 0.0318 0.045 0.0167 0.0078 0.0083 0.0057 0.0174 0.0188 0.0054 0.0114 0.0196 0.0147 0.0062 R
4、 准备数据--转换样本集
def loadDataSet(filename):
dataSet = []
with open(filename, 'r') as fs:
for line in fs.readlines():
if not line:
contine
lineArr = []
for feature in line.split(','):
str_f = feature.strip()
if str_f. isdigit():
lineArr.append(float(str_f))
else:
#添加分类标签
lineArr.append(str_f)
dataSet.append(lineArr)
return dataSet5、 分析数据--人工检查数据
6、 训练算法
在数据集上使用random_forest()函数进行优化评估,返回模型的综合分类结果。
- 交叉验证
def cross_validation_split(dataset, n_flods):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = len(dataset)/n_folds
for i in range(n_folds):
#每次循环fold清零,防止重复导入dataset_split
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy[index])
#foled.append(dataset_copy[index])
dataset_split.append(fold)
return dataset_split- 数据集随机化
#Create a random subsample ffrom the dataset with replacement.
def subsample(dataset, ratio): # 创建数据集的随机子样本
"""random_forest(评估算法性能,返回模型得分)
Args:
dataset 训练数据集
ratio 训练数据集的样本比例
Returns:
sample 随机抽样的训练样本
"""
sample = list()
# 训练样本的按比例抽样。
# round() 方法返回浮点数x的四舍五入值。
n_sample = round(len(dataset) * ratio)
while len(sample) < n_sample:
index = randrange(len(dataset))
sample.append(dataset[index])
return sample- 特征随机化
def get_split(dataset, n_features):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
features = list()
while len(features) < n_features:
index = randrange(len(dataset[0])-1)
if index not in features:
features.append(index)
for index in features:
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index': b_index, 'value': b_value, 'groups': b_groups}- 随机森林
#随机森林 Random Forest Algorithm
def random_forest(train, test, max_depth, min_size,sample_size, n_trees, n_features):
trees = list()
for i in range(n_trees):
sample = subsample(train, sample_size)#随机抽样的训练样本,随机采样保证每个决策树训练集的差异性。
tree = build_tree(sample,max_depth, min_size, n_features) #创建一个决策树
trees.append(tree)
predictions = [bagging_predict(trees, row) for row in test] #每一行的预测结果,bagging预测最后的分类结果
return predictions7、测试算法
使用自定义的n_folds份随机重抽样,进行测试评估,得到预测的综合评分情况。那么,显然是计算随机森林预测的结果的正确率情况。
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
#将数据集随机抽样,分成n_folds份,数据无重复抽取
folds = cross_validation_split(dataset, n_folds)
scores = list()
#每次循环从folds中选取一个fold作为训练数据集,遍历整个folds,进行交叉验证。
for fold in folds:
#将多个fold列表组成一个train_set列表
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set,[])
test_set = list()
#fold表示从原始数据集中提取出来的测试集
for row in fold:
row_copy = list(row)
row_copy[-1] = None
test_set.append(row_copy)
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores8、使用算法
构建完整的程序,进行测试集数据分类预测。其余代码如下:
from random import seed, randrange, random
#Split a dataset based on an attribute and an attributed value.
def test_split(index, value ,dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left ,right
#Calculate the Gini index for a split dataset
def gini_index(groups, class_values):
gini = 0.0
for class_value in class_values:
for group in groups:
size = len(group)
if size == 0:
continue
proporation = [row[-1] for row in group].count(class_value)/float(size)
gini += (proporation*(1-proporation))
return gini
#Create a terminal node value ,输出group中出现次数较多的标签。
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key = outcomes.count)
#Create child split for a node of make terminal,创建子分类器,递归分类,直到分类结束。
def split(node, max_depth, min_size, n_features, depth):
left, right = node['groups']
# Check for a no split
if not left or right :
node['left'] = node['right'] = to_terminal(left + right)
return
#check for max depth ,max_depth =10 表示递归10次,若分类还没结束,则选数据分类标签较多的作为结果,使分类提前结束,防止过拟合。
if depth >= max_depth:
node['left'] , node['right'] = to_terminal(left), to_terminal(right)
return
# process left child
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left, n_features)
split(node['left'], max_depth, min_size, n_features, detph+1)
#Build a decision tree.
def build_tree(train, max_depth, min_size, n_features):
"""
build_tree(创建一个决策树)
Args:
train--训练数据集; max_depth--决策树深度不能太深,否则会容易导致过拟合;min_size--叶子节点大小; n_features--选取特征的个数
Returns:
root --返回决策树.
"""
#返回最优列和相关信息。
root = get_split(train, n_features)
split(root, max_depth, min_size, n_features, 1)
return root
# Make a prediction with a decision tree.
def predict(node, row):
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row)
else:
return node['left']
else:
if isinstance(node['right'], dict):
return predict(node['right'],row)
else:
return node['right']
#Make a decision with a list of bagged trees.
def bagging_predict(trees, row):
"""
bagging_predict(bagging预测)
Args:
trees--决策树集合; row--测试数据集的每一行数据。
Returns:
返回随机森林中决策树结果做大的那个。
"""
# 使用多个决策树对测试集test第row行进行预测,再使用简单投票法判断出该行属于哪一个分类。
predictions = [predict(tree, row) for tree in trees]
return max(set(predictions), key = predictions.count)
#Create a accuracy percentage.
def accuracy_metric(actual, predicted):
#导入实际值和预测值,计算精确度。
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct/float(len(actual))*100.0
# 加载数据
if __name__ == '__main__':
# 加载数据
dataset = loadDataSet('sonar-all-data.txt')
# print dataset
n_folds = 5 # 分成5份数据,进行交叉验证
max_depth = 20 # 调参(自己修改) #决策树深度不能太深,不然容易导致过拟合
min_size = 1 # 决策树的叶子节点最少的元素数量
sample_size = 1.0 # 做决策树时候的样本的比例
# n_features = int((len(dataset[0])-1))
n_features = 15 # 调参(自己修改) #准确性与多样性之间的权衡
for n_trees in [1, 10, 20]: # 理论上树是越多越好
scores = evaluate_algorithm(dataset, random_forest, n_folds, max_depth, min_size, sample_size, n_trees, n_features)
# 每一次执行本文件时都能产生同一个随机数
seed(1)
print('random=', random())
print('Trees: %d' % n_trees)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores)))) 9、最后程序运行结果情况
如下:
random= 0.13436424411240122
Trees: 1
Scores: [50.0, 52.38095238095239, 47.61904761904761, 50.0, 47.61904761904761]
random= 0.13436424411240122
Trees: 10
Scores: [61.904761904761905, 59.523809523809526, 64.28571428571429, 66.66666666666666, 45.23809523809524]
random= 0.13436424411240122
Trees: 20
Scores: [61.904761904761905, 59.523809523809526, 64.28571428571429, 66.66666666666666, 45.23809523809524]
Mean Accuracy: 59.524%五、AdaBoost算法
1、adaBoost算法概述
AdaBoot是adaptive boosting(自适应boosting)的缩写,运行机制如下:
训练数据中的每个样本,并赋予一个权重,这些权重共同构成了向量D。起初,这些权重全部被初始化成相等值。首先,在训练数据集上训练出一个弱分类器并计算该分类器的错误率,然后在同一数据集上再次训练弱分类器。在分类器的第二次训练中,每个样本的权重会被重新调整,其中第一次分对的样本权重会下降,第一次分错的样本的权重被提高。为了从所有若分类器中得到最终的分类结果,AdaBoost给每个分类器都分配了一个权重值alpha,这些alpha的值是基于每个弱分类器的错误率进行计算的,alpha可以理解为弱分类器中的“话语权”。
- 训练弱分类器使其最小化权重误差函数(weighted error function)即错误率(未正确分类的样本数目/所有样本数目):
- alpha的计算公式:
- 更新权重:
- 得到最后的分类器
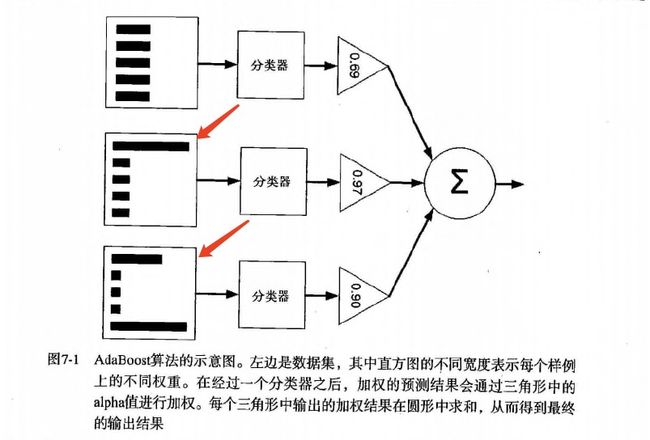
2、 AdaBoost工作原理
3、 AdaBoost开发流程
收集数据: 可以使用任意方法。
准备数据: 依赖于所使用的弱分类器类型,本文使用单层决策树,这种分类器可以处理任何数据类型。当然也可以使用任意分类器作为弱分类器。作为弱分类器,简单分类器的效果更好。
分析数据: 可以使用任意方法。
训练算法: AdaBoost大部分时间都用在训练上,分类器将多次在同一数据集上训练弱分类器。
测试算法: 计算分类的错误率。
使用算法: 同SVM一样,AdaBoost预测两个类别中的一个。若想把它应用到多个类别场合,则就要像多类SVM中的做法一样对AdaBoost进行修改。
4、 AdaBoost的相关特性
优点: 泛化错误率低,易编码,可以应用在大部分分类器上,无需调参。
缺点: 对离群点敏感。
适用数据类型: 数值型和标称型数据。
5、 完整AdaBoost算法的实现
伪代码如下:
对每次迭代:
利用buildStump()函数找到最佳的单层决策树
将最佳单层决策树加入到单层决策树组
计算alpha
计算新的权重向量D
更新累计类别估计值
若错误率等于0.0,则退出循环。
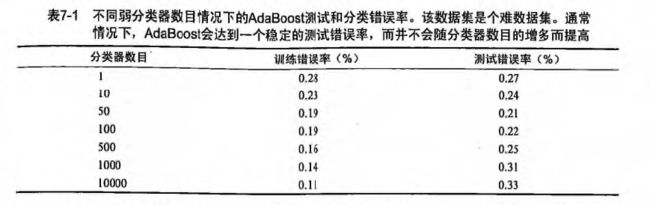
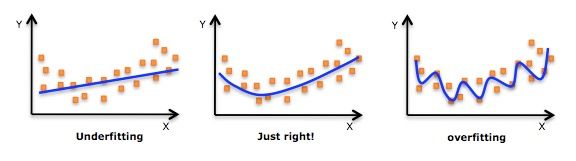
6、 过拟合(overfitting,或过学习)
如 上表测试错误率一栏所示,可以发现测试错误率在达到一个最小值之后又开始上升,这类现象称之为“过拟合(overfitting,也称过学习)”。说的直白些,过拟合就是把一些噪声也拟合进去了。如下图所示:
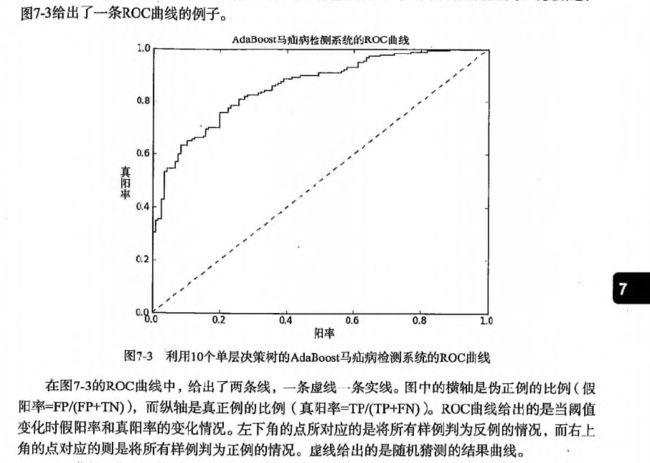
7、 ROC曲线
ROC(receiver operating characteristic)曲线用于度量分类中的非均衡性,最早在二战期间由电气工程师构建雷达系统时使用的。
六、 项目案例: 马疝病的预测
1、项目概述
预测患有疝气病的马的存活问题,这里的数据包括368个样本和28个特征,疝气病是描述马胃肠痛的术语,然而,这种病并不一定源自马的胃肠问题,其他问题也可能引发疝气病,该数据集中包含了医院检测马疝气病的一些指标,有的指标比较主观,有的指标难以测量,例如马的疼痛级别。另外,除了部分指标主观和难以测量之外,该数据还存在一个问题,数据集中有30%的值是缺失的。
2、项目流程
3、 开发流程
收集数据: 提供的文本文件
准备数据: 确保类别标签为+1和-1,而非1和0.
分析数据: 手工检查数据。
训练算法: 在数据上,使用adaBoostTrainDS()函数训练一系列的分类器。
测试算法: 这里有两个数据集。在不采用随机抽样的情况下,对AdaBoost和Logistic回归的结果进行完全对等的比较。
使用算法: 观察该例子上的错误率。
4、 收集数据--提供的文本文件
训练数据:horseColicTraining.txt和 测试数据:horseColicTest.txt,以训练数据集为例,部分数据如下:
2 1 37.5 48 24 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 37.6 64 21 1 1 2 1 2 3 1 1 1 0 2 5 40 7 1 0 1
2 1 39.4 110 35 4 3 6 0 0 3 3 0 0 0 0 0 55 8.7 0 0 1
1 1 39.9 72 60 1 1 5 2 5 4 4 3 1 0 4 4 46 6.1 2 0 1
2 1 38.4 48 16 1 0 1 1 1 3 1 2 3 5.5 4 3 49 6.8 0 0 1
1 1 38.6 42 34 2 1 4 0 2 3 1 0 0 0 1 0 48 7.2 0 0 1
1 9 38.3 130 60 0 3 0 1 2 4 0 0 0 0 0 0 50 70 0 0 1
1 1 38.1 60 12 3 3 3 1 0 4 3 3 2 2 0 0 51 65 0 0 1
2 1 37.8 60 42 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 38.3 72 30 4 3 3 2 3 3 3 2 1 0 3 5 43 7 2 3.9 1
1 1 37.8 48 12 3 1 1 1 0 3 2 1 1 0 1 3 37 5.5 2 1.3 1
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1
5、准备数据
类别标签为+1和-1而非1和0。
# general function to parse tab -delimited floats
def loadDataSet(fileName):
# get number of fields
numFeat = len(open(fileName).readline().split('\t'))
dataArr = []
labelArr = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataArr.append(lineArr)
labelArr.append(float(curLine[-1]))
return dataArr, labelArr
6、 分析数据-人工检查处理
7、训练算法
def adaBoostTrainDS(dataArr, labelArr, numIt=40):
"""adaBoostTrainDS(adaBoost训练过程放大)
Args:
dataArr 特征标签集合
labelArr 分类标签集合
numIt 实例数
Returns:
weakClassArr 弱分类器的集合
aggClassEst 预测的分类结果值
"""
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m, 1))/m)
aggClassEst = mat(zeros((m, 1)))
for i in range(numIt):
# 得到决策树的模型
bestStump, error, classEst = buildStump(dataArr, labelArr, D)
alpha = float(0.5*log((1.0-error)/max(error, 1e-16)))
bestStump['alpha'] = alpha
# store Stump Params in Array
weakClassArr.append(bestStump)
expon = multiply(-1*alpha*mat(labelArr).T, classEst)
D = multiply(D, exp(expon))
D = D/D.sum()
aggClassEst += alpha*classEst
aggErrors = multiply(sign(aggClassEst) != mat(labelArr).T, ones((m, 1)))
errorRate = aggErrors.sum()/m
# print "total error=%s " % (errorRate)
if errorRate == 0.0:
break
return weakClassArr, aggClassEst8、测试算法
def adaClassify(datToClass, classifierArr):
# do stuff similar to last aggClassEst in adaBoostTrainDS
dataMat = mat(datToClass)
m = shape(dataMat)[0]
aggClassEst = mat(zeros((m, 1)))
# 循环 多个分类器
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMat, classifierArr[i]['dim'], classifierArr[i]['thresh'], classifierArr[i]['ineq'])
aggClassEst += classifierArr[i]['alpha']*classEst
# print aggClassEst
return sign(aggClassEst)9、使用算法
if __name__ == "__main__":
dataArr, labelArr = loadDataSet("horseColicTraining2.txt")
weakClassArr, aggClassEst = adaBoostTrainDS(dataArr, labelArr, 40)
print(weakClassArr, '\n-----\n', aggClassEst.T)
# 计算ROC下面的AUC的面积大小
plotROC(aggClassEst.T, labelArr)
# 测试集合
dataArrTest, labelArrTest = loadDataSet("horseColicTest2.txt")
m = shape(dataArrTest)[0]
predicting10 = adaClassify(dataArrTest, weakClassArr)
errArr = mat(ones((m, 1)))
# 测试:计算总样本数,错误样本数,错误率
print(m, errArr[predicting10 != mat(labelArrTest).T].sum(), errArr[predicting10 != mat(labelArrTest).T].sum()/m) 10、 其他函数
from numpy import *
def loadSimpData():
""" 测试数据
Returns:
dataArr feature对应的数据集
labelArr feature对应的分类标签
"""
dataArr = array([[1., 2.1], [2., 1.1], [1.3, 1.], [1., 1.], [2., 1.]])
labelArr = [1.0, 1.0, -1.0, -1.0, 1.0]
return dataArr, labelArr
def stumpClassify(dataMat, dimen, threshVal, threshIneq):
"""stumpClassify(将数据集,按照feature列的value进行 二分法切分比较来赋值分类)
Args:
dataMat Matrix数据集
dimen 特征列
threshVal 特征列要比较的值
Returns:
retArray 结果集
"""
# 默认都是1
retArray = ones((shape(dataMat)[0], 1))
if threshIneq == 'lt':
retArray[dataMat[:, dimen] <= threshVal] = -1.0
else:
retArray[dataMat[:, dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr, labelArr, D):
"""buildStump(得到决策树的模型)
Args:
dataArr 特征标签集合
labelArr 分类标签集合
D 最初的特征权重值
Returns:
bestStump 最优的分类器模型
minError 错误率
bestClasEst 训练后的结果集
"""
# 转换数据
dataMat = mat(dataArr)
labelMat = mat(labelArr).T
# m行 n列
m, n = shape(dataMat)
# 初始化数据
numSteps = 10.0
bestStump = {}
bestClasEst = mat(zeros((m, 1)))
# 初始化的最小误差为无穷大
minError = inf
# 循环所有的feature列,将列切分成 若干份,每一段以最左边的点作为分类节点
for i in range(n):
rangeMin = dataMat[:, i].min()
rangeMax = dataMat[:, i].max()
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1, int(numSteps)+1):
# go over less than and greater than
for inequal in ['lt', 'gt']:
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMat, i, threshVal, inequal)
errArr = mat(ones((m, 1)))
# 正确为0,错误为1
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump, minError, bestClasEst
def plotROC(predStrengths, classLabels):
"""plotROC(打印ROC曲线,并计算AUC的面积大小)
Args:
predStrengths 最终预测结果的权重值
classLabels 原始数据的分类结果集
"""
import matplotlib.pyplot as plt
# variable to calculate AUC
ySum = 0.0
numPosClas = sum(array(classLabels)==1.0)
yStep = 1/float(numPosClas)
xStep = 1/float(len(classLabels)-numPosClas)
sortedIndicies = predStrengths.argsort()
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
# cursor光标值
cur = (1.0, 1.0)
# loop through all the values, drawing a line segment at each point
for index in sortedIndicies.tolist()[0]:
if classLabels[index] == 1.0:
delX = 0
delY = yStep
else:
delX = xStep
delY = 0
ySum += cur[1]
ax.plot([cur[0], cur[0]-delX], [cur[1], cur[1]-delY], c='b')
cur = (cur[0]-delX, cur[1]-delY)
ax.plot([0, 1], [0, 1], 'b--')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve for AdaBoost horse colic detection system')
ax.axis([0, 1, 0, 1])
plt.show()
print("the Area Under the Curve is: ", ySum*xStep)
11、 模型效果展示
[{'dim': 9, 'thresh': 3.0, 'ineq': 'gt', 'alpha': 0.4616623792657674}, {'dim': 17, 'thresh': 52.5, 'ineq': 'gt', 'alpha': 0.31248245042467104}, {'dim': 3, 'thresh': 55.199999999999996, 'ineq': 'gt', 'alpha': 0.2868097320169577}, {'dim': 18, 'thresh': 62.300000000000004, 'ineq': 'lt', 'alpha': 0.23297004638939506}, {'dim': 10, 'thresh': 0.0, 'ineq': 'lt', 'alpha': 0.19803846151213741}, {'dim': 5, 'thresh': 2.0, 'ineq': 'gt', 'alpha': 0.18847887349020634}, {'dim': 12, 'thresh': 1.2, 'ineq': 'lt', 'alpha': 0.15227368997476778}, {'dim': 7, 'thresh': 1.2, 'ineq': 'gt', 'alpha': 0.15510870821690512}, {'dim': 5, 'thresh': 0.0, 'ineq': 'lt', 'alpha': 0.13536197353359405}, {'dim': 4, 'thresh': 28.799999999999997, 'ineq': 'lt', 'alpha': 0.12521587326132078}, {'dim': 11, 'thresh': 2.0, 'ineq': 'gt', 'alpha': 0.1334764812820767}, {'dim': 9, 'thresh': 4.0, 'ineq': 'lt', 'alpha': 0.1418224325377107}, {'dim': 14, 'thresh': 0.0, 'ineq': 'gt', 'alpha': 0.10264268449708028}, {'dim': 0, 'thresh': 1.0, 'ineq': 'lt', 'alpha': 0.11883732872109484}, {'dim': 4, 'thresh': 19.199999999999999, 'ineq': 'gt', 'alpha': 0.09879216527106625}, {'dim': 2, 'thresh': 36.719999999999999, 'ineq': 'lt', 'alpha': 0.12029960885056867}, {'dim': 3, 'thresh': 92.0, 'ineq': 'lt', 'alpha': 0.10846927663989175}, {'dim': 15, 'thresh': 0.0, 'ineq': 'lt', 'alpha': 0.09652967982091411}, {'dim': 3, 'thresh': 73.599999999999994, 'ineq': 'gt', 'alpha': 0.08958515309272022}, {'dim': 18, 'thresh': 8.9000000000000004, 'ineq': 'lt', 'alpha': 0.09210361961272426}, {'dim': 16, 'thresh': 4.0, 'ineq': 'gt', 'alpha': 0.10464142217079622}, {'dim': 11, 'thresh': 3.2000000000000002, 'ineq': 'lt', 'alpha': 0.09575457291711606}, {'dim': 20, 'thresh': 0.0, 'ineq': 'gt', 'alpha': 0.09624217440331524}, {'dim': 17, 'thresh': 37.5, 'ineq': 'lt', 'alpha': 0.0785966288518967}, {'dim': 9, 'thresh': 2.0, 'ineq': 'lt', 'alpha': 0.0714286363455072}, {'dim': 5, 'thresh': 2.0, 'ineq': 'gt', 'alpha': 0.07830753154662214}, {'dim': 4, 'thresh': 28.799999999999997, 'ineq': 'lt', 'alpha': 0.07606159074712784}, {'dim': 4, 'thresh': 19.199999999999999, 'ineq': 'gt', 'alpha': 0.08306752811081955}, {'dim': 7, 'thresh': 4.2000000000000002, 'ineq': 'gt', 'alpha': 0.0830416741141175}, {'dim': 3, 'thresh': 92.0, 'ineq': 'lt', 'alpha': 0.08893356802801224}, {'dim': 14, 'thresh': 3.0, 'ineq': 'gt', 'alpha': 0.07000509315417908}, {'dim': 7, 'thresh': 5.3999999999999995, 'ineq': 'lt', 'alpha': 0.07697582358565964}, {'dim': 18, 'thresh': 0.0, 'ineq': 'lt', 'alpha': 0.08507457442866707}, {'dim': 5, 'thresh': 3.2000000000000002, 'ineq': 'lt', 'alpha': 0.0676590387302069}, {'dim': 7, 'thresh': 3.0, 'ineq': 'gt', 'alpha': 0.08045680822237049}, {'dim': 12, 'thresh': 1.2, 'ineq': 'lt', 'alpha': 0.05616862921969557}, {'dim': 11, 'thresh': 2.0, 'ineq': 'gt', 'alpha': 0.06454264376249863}, {'dim': 7, 'thresh': 5.3999999999999995, 'ineq': 'lt', 'alpha': 0.05308888435382875}, {'dim': 11, 'thresh': 0.0, 'ineq': 'lt', 'alpha': 0.0734605861478849}, {'dim': 13, 'thresh': 0.0, 'ineq': 'gt', 'alpha': 0.07872267320907414}]
-----
[[ -3.46206894e-01 5.39820797e-01 1.34706655e+00 -1.96577914e-01
-2.92640472e-01 1.41661959e+00 1.02056225e+00 7.09312478e-01
-6.97844480e-01 8.52681888e-01 -1.51497974e-01 1.03289265e+00
1.43744689e+00 5.23008588e-01 1.00754226e+00 -5.04904838e-01
-1.55314011e+00 3.37496140e-01 1.83380220e-01 -2.73211412e-01
1.83753941e-01 1.94948307e+00 1.36536919e+00 1.51795899e+00
4.95458633e-01 1.66431604e-01 1.58899728e-01 7.56968915e-01
2.22941652e-01 2.33498196e+00 -9.09968780e-01 -2.25738386e-02
1.02102068e+00 6.63777579e-01 -2.08699355e-01 -1.78741084e+00
-3.78931896e-01 1.31751382e-01 1.67107366e+00 1.44392330e-01
-1.99093605e+00 5.16925045e-01 6.03341572e-01 -8.92743621e-01
-1.40693534e+00 -1.12567454e+00 -1.05681881e+00 1.72070073e+00
-8.66939191e-01 -1.60476417e+00 1.36634010e+00 3.79725055e-01
1.48452270e+00 6.64838547e-01 -3.26008621e-01 9.02376775e-02
3.93090801e-01 -1.14416817e-01 -6.16067208e-01 -1.27022815e+00
1.09311484e+00 1.72115916e+00 -4.29767329e-01 8.56337614e-02
-5.03473910e-01 4.64372963e-01 4.37330130e-01 1.93105924e+00
3.76440825e-02 1.53848847e+00 -1.70686489e-01 1.65834558e+00
-1.10078594e-01 -8.87042088e-01 3.93090801e-01 -7.93642352e-02
1.53618383e+00 2.00712868e+00 -1.29429189e-01 3.01572381e-01
-7.39738757e-01 1.05727042e+00 6.20389927e-01 -1.54961074e+00
5.38841873e-02 1.97319467e+00 -1.03933604e+00 5.95474367e-01
1.07315325e+00 2.02648722e+00 8.84069009e-01 -3.26008621e-01
1.39748643e+00 1.57824639e-03 1.20825738e+00 1.30012673e+00
7.59283818e-01 -1.32980287e+00 1.58143651e+00 -7.74682670e-01
1.61012477e+00 -1.58747355e+00 7.92723052e-01 1.62137341e+00
-1.44363067e-01 7.62472658e-01 5.55115414e-01 1.76395746e+00
-8.07172746e-01 -7.13443067e-01 -7.62149648e-01 1.06275540e+00
1.18148515e+00 -6.66282330e-01 2.36684357e-01 1.89994809e+00
2.24478748e+00 -9.17624883e-02 2.96253630e-01 1.08742569e+00
1.36883746e+00 -1.13525331e+00 1.80620011e+00 -5.59442382e-01
3.73123890e-01 1.84054205e+00 1.06799214e-01 5.89414867e-01
-6.54353819e-01 1.19724374e+00 4.63540870e-01 3.74879494e-01
1.47856059e+00 -6.57446519e-01 -6.93668829e-01 -1.29429189e-01
1.31594962e+00 1.64420444e+00 9.53502459e-01 7.40170420e-01
-4.35385025e-01 -1.30434214e+00 1.65834558e+00 -1.61422920e-01
7.50544036e-01 1.50390920e+00 8.12006783e-01 -1.11433828e-01
1.58948356e+00 1.80166124e+00 -1.24848181e+00 -3.16358922e-01
1.39748643e+00 2.36697540e+00 5.45445830e-01 1.30735427e+00
6.47538358e-01 1.16305757e+00 1.74396199e+00 -7.62381985e-01
4.27163890e-01 1.51465087e+00 -1.12436666e-01 8.09957092e-01
7.23764279e-03 1.94052195e+00 1.48306468e+00 2.64418198e-01
-1.21867130e+00 1.20420927e+00 -1.30937256e+00 -4.84404331e-01
-1.34263866e+00 -1.01739294e+00 2.22941652e-01 2.00510724e+00
-2.29750158e+00 -3.83556393e-01 -7.55614485e-01 -1.34943874e+00
8.51461579e-01 -1.54961074e+00 1.86860473e+00 2.09992462e+00
-4.31918141e-01 9.12376049e-01 1.32753580e-01 1.05799984e+00
3.94948721e-01 8.84028367e-01 5.37930835e-01 1.84470134e+00
-1.78544316e+00 6.35626744e-01 2.15191386e+00 -9.72238538e-02
1.90924894e-01 1.59095456e+00 8.40972426e-01 1.49370558e+00
-5.84176145e-01 4.54713517e-01 2.13758537e+00 -3.16164749e-01
-7.55614485e-01 5.31183150e-01 5.50284059e-01 -4.07776113e-01
2.05323133e+00 -1.22382729e-01 -9.51971888e-01 7.76212308e-01
1.02082939e+00 1.72495570e+00 2.05710397e+00 4.60616309e-01
-4.02664156e-01 8.58959865e-01 3.77072878e-02 -6.71174191e-01
7.47080450e-01 -3.81125550e-01 1.12389210e+00 1.75800100e+00
1.73857489e+00 -1.33101576e+00 5.50284059e-01 -1.30289376e+00
1.31228529e+00 -5.60455028e-01 -1.46354481e+00 7.90883276e-01
1.58899728e-01 1.20825738e+00 -8.87042088e-01 1.65728396e+00
1.22103595e+00 2.14912978e-01 3.64699577e-02 -1.32127479e+00
1.33000192e+00 -4.70065248e-02 -4.22251353e-02 7.70710258e-01
-1.27022815e+00 -8.61045169e-01 -9.56969900e-01 -7.95783983e-02
2.08738328e+00 -4.85855645e-01 3.91162341e-01 2.72751462e-01
-6.20974162e-01 -5.83646639e-01 1.44817145e-01 1.36706959e+00
-1.21222173e+00 1.92002542e+00 1.70722977e-01 9.55937244e-01
1.70564235e+00 -2.45144481e-01 -5.56039012e-01 1.94646186e-01
1.12867995e+00 5.63912150e-01 4.95748848e-01 1.20050741e+00
5.50857009e-01 6.29115697e-01 -1.11443306e-01 -2.08699355e-01
-1.63615949e+00 -4.00661971e-01 2.54103847e-01 8.38248031e-01
1.32784858e+00 1.87814608e+00 2.34862459e-01 1.67991427e+00
-6.70647873e-01 -7.62149648e-01 6.00705546e-02 2.24515155e+00
1.05333955e+00 -1.17411061e+00 1.57410447e-01 2.22941652e-01
1.51614920e+00 1.76240799e+00 -8.66939191e-01 -9.92873427e-01
-4.92052272e-01 2.52829341e+00 -1.55549790e-01 -1.18640330e+00
-1.35781920e+00 -1.94654268e-01 4.54752882e-01]]
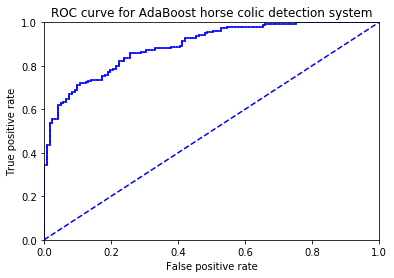
the Area Under the Curve is: 0.8918191104095092
67 13.0 0.194029850746七、 小结
集成方法通过组合多个分类器的分类结果,得到比简单的单分类器更好的分类结果。当然,也有一些利用不同分类器的集成方法。
多个分类器组合可能会进一步凸显出单分类器的不足,例如过拟合问题。遇到多分类器之间差异显著的化,则多个分类器组合会缓解这一问题。分类器之间的差别,可以是算法本身或者是应用于算法上的数据不同。
本文介绍了两种集成方式--bagging和boosting。bagging中,是通过随机抽样的替换方式,得到了与原始数据集规模一样的数据集;而boosting是在bagging的基础上更进一步,它在数据集上顺序应用了多个不同的分类器。而boosting中最流行的一个算法是AdaBoost算法。AdaBoost以弱学习为基础分类器,且输入数据,使其通过权重向量进行加权。第一次迭代中,所有数据都等权重,但后续迭代中,前次迭代中分错的数据权重会增大。这里针对错误的调节能力正是AdaBoost的优势。
非均衡分类问题是指在分类器训练时正例数目和反例数目不相等且相差很大。用于度量分类中的非均衡性的工具之一是ROC曲线。
截止目前,笔者已经梳理了一系列相当不错的分类技术,都是属于监督分类方面的技术。由于笔者水平有限,有不足之处,请各位多多指点。