java二叉树的各种遍历详解
想了解更多数据结构以及算法题,可以关注微信公众号“数据结构和算法”,每天一题为你精彩解答。也可以扫描下面的二维码关注

基础知识
树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点,也就是说除了根节点以外每个节点都有父节点,并且有且只有一个。
树的种类比较多,有二叉树,红黑树,AVL树,B树,哈夫曼树,字典树等等。
甚至堆我们也可以把它看成是一棵树,树的这么多种类中,我们最常见的应该是二叉树了,下面我们来看一下他的结构。
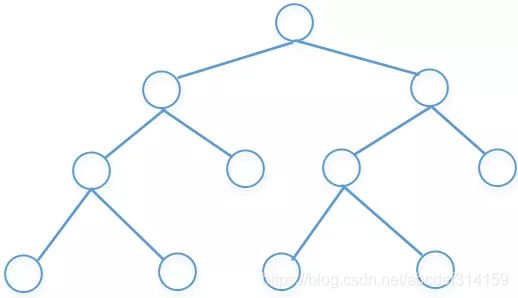
定义:
1,结点的度: 一个结点含有的子结点的个数称为该结点的度;
2,叶结点或终端结点: 度为0的结点称为叶结点;
3,非终端结点或分支结点: 度不为0的结点;
4,双亲结点或父结点: 若一个结点含有子结点,则这个结点称为其子结点的父结点;
5,孩子结点或子结点: 一个结点含有的子树的根结点称为该结点的子结点;
6,兄弟结点: 具有相同父结点的结点互称为兄弟结点;
7,树的度: 一棵树中,最大的结点的度称为树的度;
8,结点的层次: 从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
9,树的高度或深度: 树中结点的最大层次;
10,堂兄弟结点: 双亲在同一层的结点互为堂兄弟;
11,结点的祖先: 从根到该结点所经分支上的所有结点;
12,子孙: 以某结点为根的子树中任一结点都称为该结点的子孙。
13,森林: 由m(m>=0)棵互不相交的树的集合称为森林;
14,无序树: 树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树;
15,有序树: 树中任意节点的子结点之间有顺序关系,这种树称为有序树;
16,二叉树: 每个节点最多含有两个子树的树称为二叉树;
17,完全二叉树: 若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
18,满二叉树: 除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
19,哈夫曼树: 带权路径最短的二叉树称为哈夫曼树或最优二叉树;
应用:
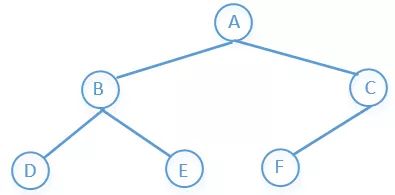
树的种类实在是太多,关于树的算法题也是贼多,这一篇文章不可能全部介绍完,我们需要具体问题再具体分析。这里主要介绍的是二叉树,并且只介绍树的一些最基础的几个算法。我们先来看个图
节点类
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) {
val = x;
}
public TreeNode() {
}
@Override
public String toString() {
return "[" + val + "]";
}
}
前序遍历
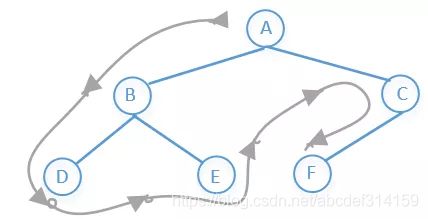
他的访问顺序是:根节点→左子树→右子树
所以上图前序遍历的结果是:A→B→D→E→C→F
访问顺序如下
public static void preOrder(TreeNode tree) {
if (tree == null)
return;
System.out.printf(tree.val + "");
preOrder(tree.left);
preOrder(tree.right);
}
非递归的写法
public static void preOrder(TreeNode tree) {
if (tree == null)
return;
Stack<TreeNode> q1 = new Stack<>();
q1.push(tree);//压栈
while (!q1.empty()) {
TreeNode t1 = q1.pop();//出栈
System.out.println(t1.val);
if (t1.right != null) {
q1.push(t1.right);
}
if (t1.left != null) {
q1.push(t1.left);
}
}
}
中序遍历
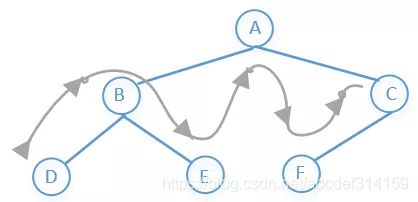
他的访问顺序是:左子树→根节点→右子树
所以上图前序遍历的结果是:D→B→E→A→F→C
访问顺序如下
public static void inOrderTraversal(TreeNode node) {
if (node == null)
return;
inOrderTraversal(node.left);
System.out.println(node.val);
inOrderTraversal(node.right);
}
非递归的写法
public static void inOrderTraversal(TreeNode tree) {
Stack<TreeNode> stack = new Stack<>();
while (tree != null || !stack.isEmpty()) {
while (tree != null) {
stack.push(tree);
tree = tree.left;
}
if (!stack.isEmpty()) {
tree = stack.pop();
System.out.println(tree.val);
tree = tree.right;
}
}
}
后续遍历
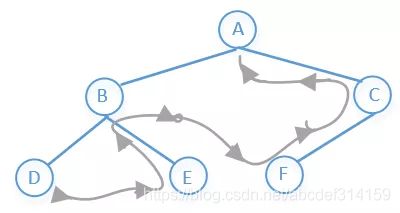
他的访问顺序是:左子树→右子树→根节点
所以上图前序遍历的结果是:D→E→B→F→C→A
访问顺序如下
public static void postOrder(TreeNode tree) {
if (tree == null)
return;
postOrder(tree.left);
postOrder(tree.right);
System.out.println(tree.val);
}
非递归的写法
public static void postOrder(TreeNode tree) {
if (tree == null)
return;
Stack<TreeNode> s1 = new Stack<>();
Stack<TreeNode> s2 = new Stack<>();
s1.push(tree);
while (!s1.isEmpty()) {
tree = s1.pop();
s2.push(tree);
if (tree.left != null) {
s1.push(tree.left);
}
if (tree.right != null) {
s1.push(tree.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().val + " ");
}
}
或者
public static void postOrder(TreeNode tree) {
if (tree == null)
return;
Stack<TreeNode> stack = new Stack<>();
stack.push(tree);
TreeNode c;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && tree != c.left && tree != c.right) {
stack.push(c.left);
} else if (c.right != null && tree != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().val + " ");
tree = c;
}
}
}
BFS(宽度优先搜索(又称广度优先搜索))
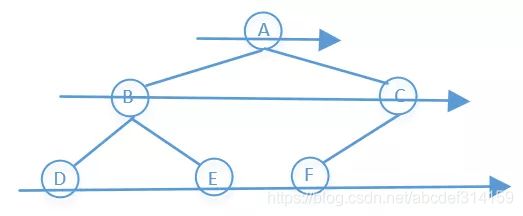
他的访问顺序是:先访问上一层,在访问下一层,一层一层的往下访问
所以上图前序遍历的结果是:A→B→C→D→E→F
访问顺序如下
public static void levelOrder(TreeNode tree) {
if (tree == null)
return;
LinkedList<TreeNode> list = new LinkedList<>();//链表,这里我们可以把它看做队列
list.add(tree);//相当于把数据加入到队列尾部
while (!list.isEmpty()) {
TreeNode node = list.poll();//poll方法相当于移除队列头部的元素
System.out.println(node.val);
if (node.left != null)
list.add(node.left);
if (node.right != null)
list.add(node.right);
}
}
递归的写法
public static void levelOrder(TreeNode tree) {
int depth = depth(tree);
for (int level = 0; level < depth; level++) {
printLevel(tree, level);
}
}
private static int depth(TreeNode tree) {
if (tree == null)
return 0;
int leftDepth = depth(tree.left);
int rightDepth = depth(tree.right);
return Math.max(leftDepth, rightDepth) + 1;
}
private static void printLevel(TreeNode tree, int level) {
if (tree == null)
return;
if (level == 0) {
System.out.print(" " + tree.val);
} else {
printLevel(tree.left, level - 1);
printLevel(tree.right, level - 1);
}
}
如果想把遍历的结果存放到list中,我们还可以这样写
public static List<List<Integer>> levelOrder(TreeNode tree) {
if (tree == null)
return null;
List<List<Integer>> list = new ArrayList<>();
bfs(tree, 0, list);
return list;
}
private static void bfs(TreeNode tree, int level, List<List<Integer>> list) {
if (tree == null)
return;
if (level >= list.size()) {
List<Integer> subList = new ArrayList<>();
subList.add(tree.val);
list.add(subList);
} else {
list.get(level).add(tree.val);
}
bfs(tree.left, level + 1, list);
bfs(tree.right, level + 1, list);
}
DFS(深度优先搜索)
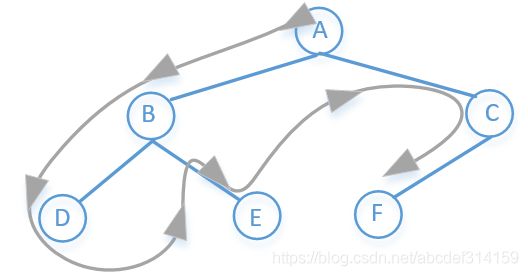
他的访问顺序是:先访根节点,然后左结点,一直往下,直到最左结点没有子节点的时候然后往上退一步到父节点,然后父节点的右子节点在重复上面步骤……
所以上图前序遍历的结果是:A→B→D→E→C→F
访问顺序如下
public static void treeDFS(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.empty()) {
TreeNode node = stack.pop();
System.out.println(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
递归的写法
public static void treeDFS(TreeNode root) {
if (root == null)
return;
System.out.println(root.val);
treeDFS(root.left);
treeDFS(root.right);
}