自然语言处理(NLP)-1.1 监督学习与情感分析(Supervised ML & Sentiment Analysis)

1.监督学习与情感分析（Supervised ML & Sentiment Analysis）

1.1监督学习

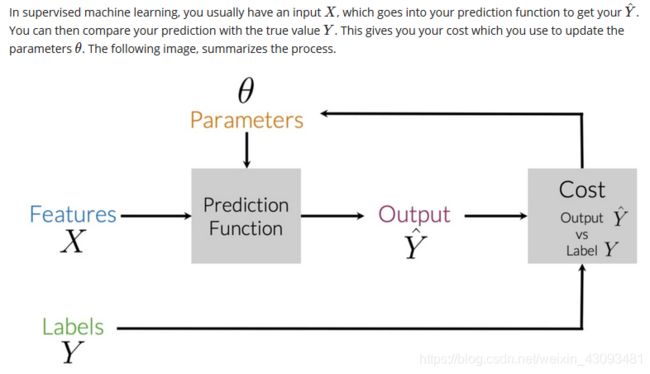
    输入：在监督学习中，需要输入特征(Features)和对应的标签(Labels)

    目的：尽可能减少损失值，使模型能较精准预测结果

    简要流程：

        (1)将特征X输入预测函数(模型)中，计算得到对应的预测标签

        (2)通过损失函数计算Y与之间的差异，即损失值(loss)，损失值越小，说明模型效果越好，预测越准确

        (3)通过损失值来更新参数

        (4)重复上述流程，直到损失值下降到理想程度

   

1.2情感分析

    目的：分辨一句话是积极的还是消极的

    简要流程：

        (1)特征提取：将原文进行一定处理，提取出有效特征，并对其进行标注(正面情感标为1，负面情感标为0)

        (2)训练逻辑回归分类器，并多次迭代减小损失值

        (3)使用训练好的模型进行预测

   

1.3 学习成果

    通过学习本课内容，能够利用监督学习(逻辑回归)的方法，构建出一个简单的情感分析模型，并可自行输入文本进行测试

    具体代码见文尾

---

2.数据处理

2.1 整体流程

    (1)预处理：将原始文本变为由单词构成的数组

    (2)特征提取：将单词数组通过计算得到特征向量

       

    (3)矩阵化：对多个数据进行上述处理，得到m个特征向量，将其拼接成矩阵形式，即得到最终需要的模型输入

       

2.2 预处理（Preprocessing）

    功能：消除文本中无意义的符号和单词等，使模型能更有效的提取特征

    流程：

        (1)去除URLs与@内容

        (2)分词：将句子拆分为一个个单词

        (3)去停用词：删除全部包含在停用词词典中的词

        (4)去标点：删除所有包含在停用标点词典中的标点

        (5)词根化：将所有词转化成其词根形式

        (6)小写化：将所有字母转化为小写

    

2.3 特征表示与特征提取

功能：显然若直接将文本输入模型中，机器是无法理解和处理的，因此需要通过一些方法，将文本转变为机器能理解和操作的格式，即特征表示与特征提取

2.3.1特征表示方法

    1.稀疏矩阵表示法：

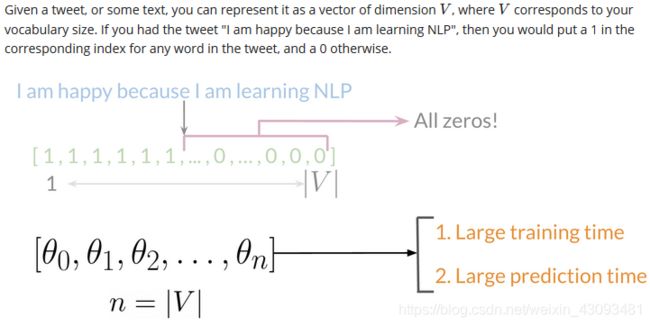
        方法：为了用向量表示文本，首先需要建立一个词汇表(Vocabulary)，表中每个位置对应一个单词，文本中出现的单词位置值为1，未出现的单词位置值为0，以此将文本转换为数组矩阵

        例子：

            

        问题：

            (1)表示的稀疏性：对于一个长度为V的句子，则需要用一个长度为V的向量进行表示，且其中有大量的0，为无效信息

            (2)时间花费高：模型中存在大量参数，因此需要大量训练时间和预测时间

            

    2.词频表示法：

        方法：

            (1)正向/负向文本分类：将语料库中文本分为正向文本和负向文本

                

            (2)频率编码：对于语料库中每个单词，分别统计其在正向文本和负向文本中出现的次数

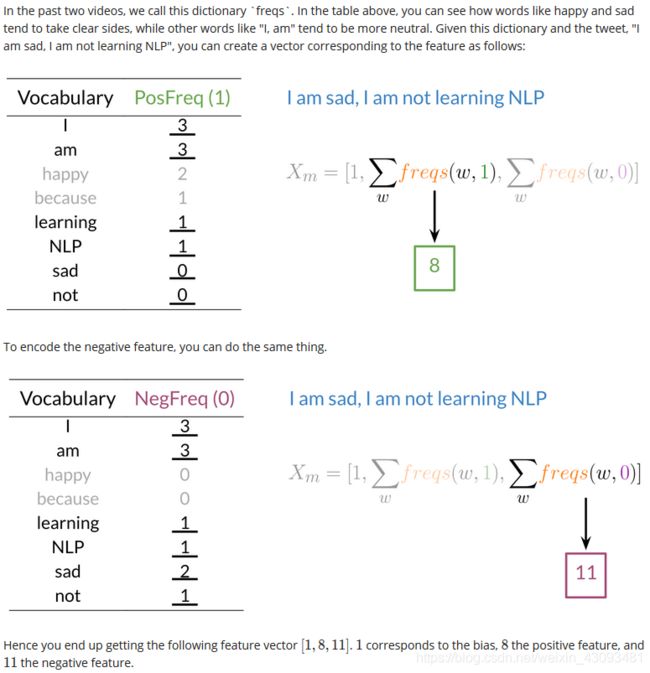
                例如：Voc[(I,PosFreq)]=3，Voc[(I,NegFreq)]=3，即表示I在正向文本和负向文本中分别出现了3次

                           Voc[(happy,PosFreq)]=2，Voc[(I,NegFreq)]=0，表示happy在正向文本中出现2次，负向文本中出现1次

                

            (3)特征提取：
                将每个文本表示成一个三元向量 [bais,PosFreq,NegFreq]，由以下三部分构成：

                    bais偏置：固定置为1

                    PosFreq正向词频：文本中各单词的正向词频和

                    NegFreq负向词频：文本中各单词的负向词频和

                例如：

                    如下图文本中，各单词在正向词频中出现的次数分别为3、3、0、0、1、1，和为8；(注：不计算重复单词)

                    各单词在正向词频中出现的次数分别为3、3、2、1、1、1，和为11

                    因此，该文本的特征向量为[1,8,11]

               

---

3.逻辑回归（Logistic Regression）

根据机器学习三要素，任何模型都由模型、学习准则(策略)、优化算法(算法)构成，其含义如下：

    模型：一个映射函数，输入数据输出预测结果，即该机器学习方法的功能和目的

    学习准则：评价模型好坏的标准，预测值与真实值的差异的期望，可以认为是损失函数

    优化算法：一个最优化问题，寻找最优模型的方法，即最小化损失函数的方法，机器学习的训练过程就是求解最优化问题的过程

3.1 模型

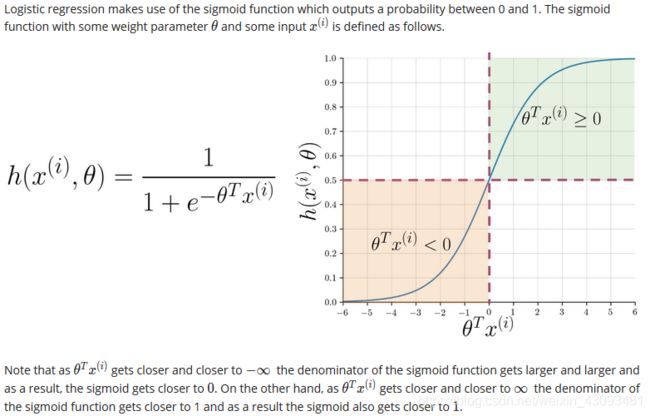
Sigmoid函数

    功能：将任意输入映射到0~1的区间，即表示概率

        

3.2 学习准则/策略

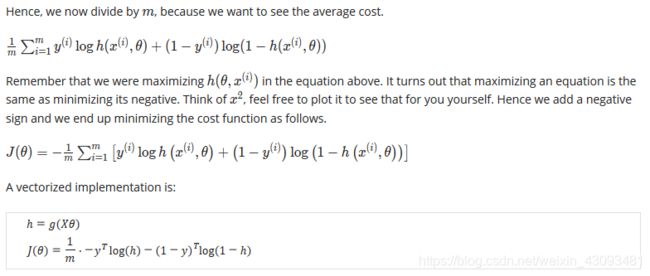
损失函数：交叉熵损失函数

    定义：

        对于1类：预测值越接近1，值越小

        对于0类：预测值越接近0，值越小

        因此，最小化损失函数J(θ)，就是最小化两类别预测错误的概率

       

    数学原理(选修)：

     

   

3.3 优化算法/算法

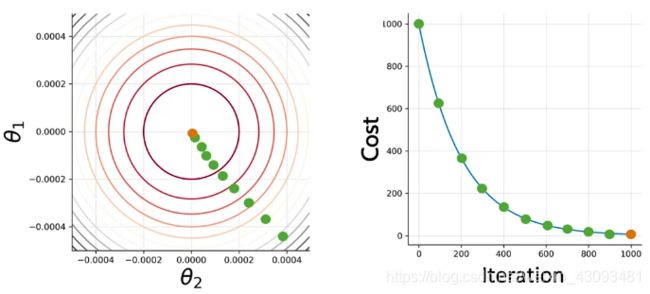
梯度下降法

    概述：是最简单、最常用的优化算法，通过计算偏导数来不断更新参数

       

    数学原理(选修)：

        定义：

           

        计算：

           

---

4.应用逻辑回归进行情感分析

4.1 方法

    将文本转化为特征向量，输入sigmoid函数进行计算，若最终结果大于0.5则为正向情感，反之为负向情感

        

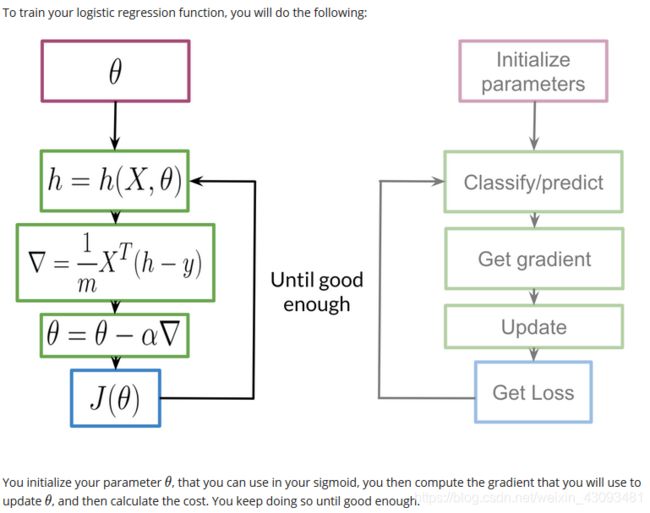
4.2 训练过程

训练过程：

    (1)初始化参数

    (2)将数据输入sigmoid函数进行计算，得到预测结果

    (3)使用梯度下降法计算更新量

    (4)利用更新量更新参数

    (5)得到损失值

    (6)重复上述过程，直到损失值最小

    

4.3 模型评价

    计算预测结果向量：

        将预测结果与设定的阈值(0.5)进行比较，若大于0.5则置为1表示正向情感，反之置为0表示负向情感

        

    计算准确率：

        即求预测正确数据占总数据比例

        

---

5.编程实战

作业/编程实战：使用逻辑回归实现情感分类

代码：https://github.com/Ogmx/Natural-Language-Processing-Specialization

内容汇总：https://blog.csdn.net/weixin_43093481/article/details/114989382

可将代码与数据下载至本地，使用jupyter notebook打开