从锁存器到简单计算机系统(备忘自用)
从触发器到简单计算机系统
19年的笔记,上传一下(●’◡’●),参考书籍如下
高等教育出版社《数字电子技术基础( 第六版 ) 》 阎石
电子工业出版社《编码:隐匿在计算机背后的语言》 佩挫
一个可编程的完整微处理系统其本质上还是从触发器开始,慢慢向上构建而成。
触发器到锁存器
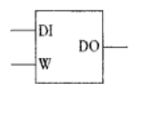
上图为一个电平D型触发器(又称D型锁存器)。当Write端置为高电平时,输出Do将被置为与Di相同的状态。
试想一下,如果我们需要找些什么东西用来存放一些数字,很自然地,我们使用刚刚介绍过的D触发器组成下面的结构,我们称之为8位锁存器。显然,我们找到了可以有效存放数字的容器(虽然是二进制数字)。(tips:因为这个图画起来肥肠麻烦,所以就有了简化版)
锁存器到RAM
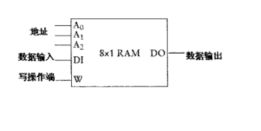
可以注意到上图中的小框写了 8x1 RAM 的字样。实际上,由于框选择器和译码器具有相同的地址端口,译码器将决定其中的哪一个D触发器能够接收数据输入;而选择器将决定输出其中哪一个D触发器的数据。经过这种配置下的锁存器的的确确可以视作为Random Access Memory,即RAM。(上面的这个存储器就是一个能够储存8个独立字节的RAM)
继续套娃
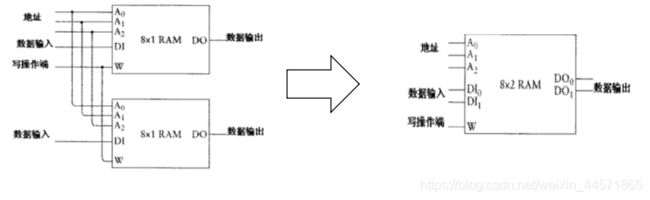
容量不够咋办,加译码器啊!(妈妈再也不用担心.jpg)比如上方的例子中,4个256X8的RAM通过2-4译码器连接后,我们得到了一个1024X8的RAM,它可以储存8192比特的信息,其中,每8个比特一组,共1024组。因此,从计算机组成的角度来讲,这个RAM阵列的容量为1024个字节,也就是1KB(kilobyte);
(注:由于图片搜寻自网络,不配套的情况在所难免。上方中的左图输入输出复用同一根线,而通过CLK时钟线来区别读/写。右图中的输入与输出线是分立的。)
带RAM的加法器
在数字电子技术的学习过程中,我们都接触过一种由逻辑门电路构成的加法器。事实上,正是加法器构成了CPU的基本运算单元(组成CPU的两个基本单元是运算器和加法器)。现在,我们将结合RAM对我们的运算器进一步优化直至组成一个完整的微处理器。
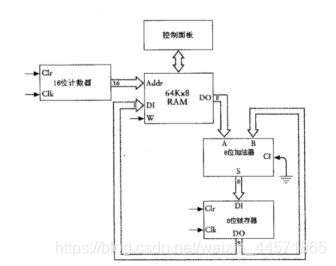
上面是我用画图软件画的一个简易加法器的框图。它使用了振荡器,计数器,和我们刚刚组成的RAM还有一个加法器以及用作输出显示8只LED灯。当然了,它看起来不是那么的好用。(不过它是有重要意义的,具体可看计算机发展史早期的计算机的系统结构…)
让我们来看看它是怎么工作的吧:
- 首先,想要使用它,必须先将清零信号置1。这样的目的是清除8位锁存器的内容并将16位计数器的输出(RAM接收的地址)置为0000h。接下来,你可以从控制端输入你需要累加的数。假设你需要累加100个数字,那么这些数将可以从0000h一直存放到0063h。接下来令清零信号置0,电路开始工作。
- 显然,每当一个时钟信号后,8位锁存器都会输出当前的值给LED显示;同时,加法器又接收到当前的值等待下一个时钟信号的到来。
- 这个电路一个巨大缺陷是我们没有办法使它自行停下来。在刚才的例子中,如果电路累加完了100个数之后,你可以通过8只LED以二进制方式读取运算结果。但前提是时钟信号足够慢,一旦计数器达到FFFFh后,它会重新回到0000h,可以想见的是,加法器会把刚才加过的数重新加一遍。
- 除此之外,这个电路只能进行加法运算。并且要求RAM中存放的数不能超过255,且运算的结果也不能超过255。如果要求减法运算(用补数代替负数),那么运算范围将进一步被限制在-128-127之间。而且,这个电路不能保存计算的结果,因为最终的输出并没有回到RAM中。为了解决这些问题,我们把输出的LED指示去掉,将输出回接到RAM。
带RAM的加法器改进版
改进后的电路如下图所示(图片来自《编码:隐匿在计算机背后的语言》)
事实上,这个电路仍没有很好的解决刚才的问题。举例来说,如果我们要想计算3B3D112Dh和2A3D9CA1h的和。由于一个字节中只能存放8位数据,我们需要把3BCD11HDh拆成3Bh、3Dh,11h和2Dh四个数,同时被加数也需要被拆成四个数。由于16计数器将顺序寻址。因此,一个可行的方案是下面这样:
如表所示,在电路工作前按表格中的格式在RAM中预先填入好数据。待电路工作后,我们会在0002h中得到最高两位的结果,不过此时需要外置电路要将8位锁存器的值清零(这可通过一些基本的逻辑门电路实现),以免后续发生累加。以此类推,我们可以得到运算的结果。和最开始的加法运算电路一样,这个电路也不能自行停止且当两数相加发生进位时会导致运算出错。而且引出了新的问题:我们运算的结果被分配到了不同的地址位上,以至于我们没法读取它们。
使用代码的加法器
那咋搞呢?(ಡωಡ)
咳咳,我想上面的表格是不是给了你一点思路,如果你曾看到过汇编代码的形式的话。
事实上,为了解决上面的问题,一种使用代码的机器诞生了,它是怎么诞生的,以及为什么诞生,这就得提到冯·诺依曼(John von Neumann,1903年12月28日-1957年2月8日)
词条戳这-> 约翰·冯·诺依曼.
美籍匈牙利科学家冯·诺依曼最先提出程序存储的思想,并成功将其运用在计算机的设计之中,根据这一原理制造的计算机被称为冯·诺依曼结构计算机。由于他对现代计算机技术的突出贡献,因此冯·诺依曼又被称为“现代计算机之父”。
这里还是使用《编码:隐匿在计算机背后的语言》中的图片形式(用画图软件画的)
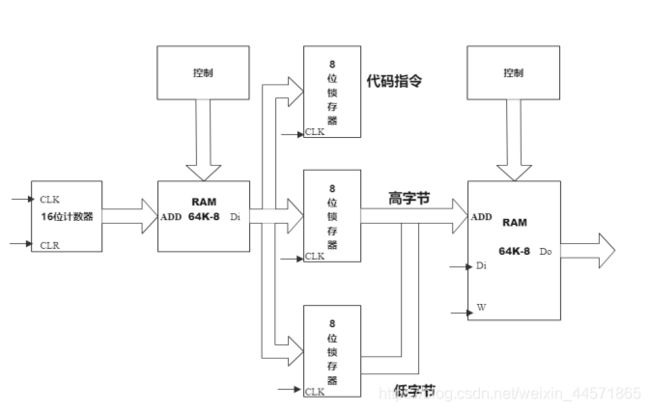
如图所示,新的计算器在原来的基础上增加了1片RAM用来存放代码,我们省略了加法器以及一些外围逻辑电路,这样可以使图更加清晰易懂。在新的设备中,计数器用来加载代码,而我们的代码由3字节的8位二进制数组成(2位16进制)。其中,第一个字节用来存放代码本身;第二个字节用来存放地址的高八位;第三个字节用来存放地址的低八位。
以11HDh和112Dh为例,新的机器将像这样执行他们的相加过程。不过在开始之前,我们需要规定一下我们的代码。比如我们规定01h为将数据装入累加器;02h为将累加器上数据填入到RAM;11h为加法;12h为进位加法。假设11HDh按照低位到高位存放在1000h处,112Dh也按照低位到高位存放在2000h处。如果代码从1000h处开始,那么,下面演示如何将它们相加并保存至3000h处。
//1
1000h:01h //把1001h处的数据装入累加器 (低位)
1001h:10
1002h:01h
//2
1003h:11h //累加器加上2001h处的数据
1004h:20
1005h:01h
//3
1006h:02h //取出累加器的数据保存到3001h
1007h:30
1008h:01h
//4
1009h:01h //把1000h处的数据装入累加器 (高位)
1010h:10
1011h:00h
//5
1012h:12h //累加器进位加上2000h处的数据(进位来自上次运算)
1013h:20
1014h:00h
//6
1015h:02h //取出累加器的数据保存到3000h
1016h:30
1017h:00h
至此,我们完成了11HDh和112Dh的加法运算并将结果保存至第二片RAM的3000h处。但这种代码实在不是给人读的,所以我们考虑使用贴近人类语言的方式重新描述它,当我们需要使用时,再将其翻译成机器码送入处理端,这也就是汇编语言的由来。
| 操作码 | 代码 |
|---|---|
| Load | 10h |
| Store | 11h |
| Add | 20h |
| Add with carry | 22h |
| Subtract | 21h |
| Subtract with borrow | 23h |
| Jump if zero | 30h |
| Jump if carry 31h | |
| Jump if no zero | 32h |
| Jump if no carry | 33h |
| Halt | FFh |
书中给出了上表这些操作码,其中借位减法原理同进位加法类似。关于halt指令和jump指令,正是这两个指令让新的设备可以与前述的加法器有了本质的区别,因为在它们的帮助下我们可以实现循环、跳转和判断。而加法器不能。
Halt将停止计数器的计数,我们可以通过在计数器的时钟信号附加逻辑门电路实现。
jump指令则可以通过计数器的预置实现,条件跳转则需要附加相应的逻辑门电路。
下面演示如何编码让机器进行乘法运算(书上的例子)
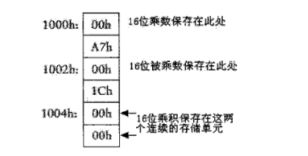
假设需要计算A7h和1Ch的乘积,使其在地址这样放置:
那么使用书上的操作码实现乘法的过程应该是这样的~(:—
000h: Load 1005h //装载预结果的低位到累加器
Add 1001h //加上被乘数的低位
Store 1005h //保存到预结果到1005h
Load 1004h //装载预结果的高位到累加器
Add with carry 1000h //进位加上被乘数的高位(进位来自低位运算)
Store 1004h //保存到预结果到1004h
Load 1003h //装载乘数
Add 001Eh //加上001Eh的数据(实际相当于减一)
Store 1003h //保存乘数减一的值
Jump if not zero 1000h //若累加器的输出不全为0,则跳转到000h继续执行
001Eh:Halt(FFh) //停止
在上面的所有的例子中,我们一直使用机器码或者英文短语来描述机器操作,这也被称作编码(coding)或编程(writing program)。
但是,没有人希望使用上面的语言进行实际的操作,于是,汇编语言(assembly language)出现了,不过,汇编语言仍是面向机器的语言,很难从其代码上理解程序设计意图,设计出来的程序不易被移植,故不像其他大多数的高级计算机语言一样被广泛应用。所以在高级语言高度发展的今天,它通常被用在底层,通常是程序优化或硬件操作的场合。
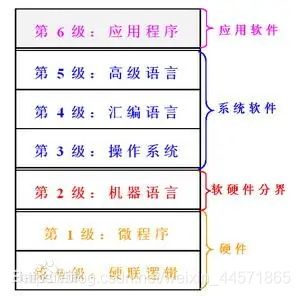
通常还把除硬件系统之外的其余层称为虚拟机,各层次之间关系密切,上层是下层的拓展,下层是上层的基础,各层次之间的划分也不是绝对的。(唐朔飞 《计算机组成原理》)
总结
至此,我们完成了一个微处理系统中的处理器和RAM部分,但是搭建一个完整的系统还需要外设(peripheral)也就是各种输入设备和输出设备(input device&output device)。而所有这些器件的通信就通过总线(Bus)实现。通常把这信号分为5类:
- 数据总线(Data Bus):在CPU与RAM之间来回传送需要处理或是需要储存的数据。
- 地址总线(Address Bus):用来指定在RAM之中储存的数据的地址。
- 控制总线(Control Bus):将微处理器控制单元(Control Unit)的信号,传送到周边设备。
- 扩展总线(Expansion Bus):外部设备和计算机主机进行数据通信的总线,例如ISA总线,PCI总线。
- 局部总线(Local Bus):取代更高速数据传输的扩展总线
学习总线,除了认识到总线的基本分类和总线传输的基本原理外,还可以给我们阅读一些芯片相关文档提供帮助,方便我们快速了解一款产品具有那些功能和外设,从而快速开发。比如下面这块典型的MCU(STM32F103xx增强型)的结构框图:
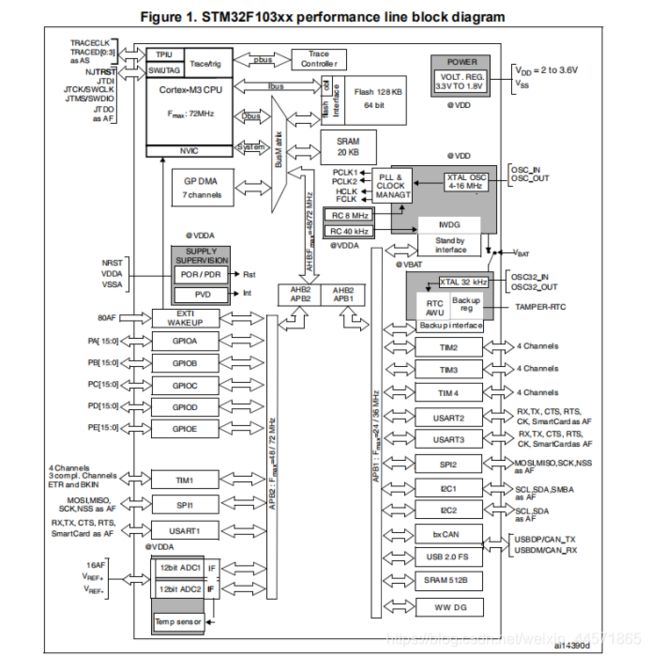
更具体的总线内容就不放在这里了
结束
byebye~