PCL 计算点云法向量并显示
目录
- 一、算法原理
-
- 1、法向量估计
- 2、法向量定向
- 3、表面曲率
- 4、参考文献
- 5、法向量定向的理解
- 6、CloudCompare
- 二、pcl::Normal的定义
- 三、pcl::Normal的几种输出方式
- 四、计算法线并显示
-
- 1、代码图解
- 2、计算输入点云的所有点的法线
- 3、计算输入点云数据中一个子集的法线
- 4、特殊操作
- 五、使用OMP的报错处理
- 六、结果展示
一、算法原理
强调一下:
- PCL中计算法向量的方法有两种,其中一种就是本文pcl::NormalEstimation中的方法;
- 该方法是基于PCA主成分分析法实现的;
- 最小二乘拟合邻域平面时用的是KD树查找邻域点。
1、法向量估计
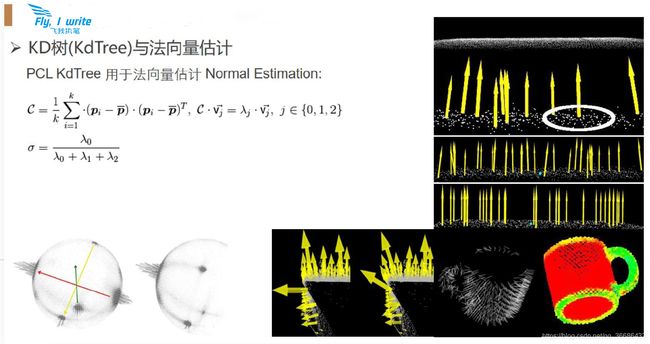
基于局部表面拟合的方法进行法向量估计:点云的采样表面处处光滑的情况下,任何点的局部邻域都可以用平面进行很好的拟合;为此,对于点云中的每个扫描点 p p p,搜索到与其最近邻的 K K K个相邻点,然后计算这些点最小二乘意义上的局部平面 P P P,此平面可以表示为:
P ( n ⃗ , d ) = arg min ( n ⃗ , d ) ∑ i = 1 k ( n ⃗ ⋅ p i − d ) 2 (1) P(\vec{n},d)=\argmin \limits_{(\vec{n},d)} \sum_{i=1}^k\ (\vec{n}\cdot p_i-d)^2\tag{1} P(n,d)=(n,d)argmini=1∑k (n⋅pi−d)2(1)
式中, n ⃗ \vec{n} n为平面 P P P的法向量, d d d为 P P P到坐标原点的距离。
可以认为由 K K K个最近点拟合出的平面的法向量即当前扫描点的法向量。平面 P P P的法向量可以由主成分分析(PCA)得到,由运算知 P P P经过其 K K K邻域点的质心 P 0 P_0 P0,且法向量 n ⃗ \vec{n} n满足 ∣ ∣ n ⃗ ∣ ∣ = 1 ||\vec{n}||=1 ∣∣n∣∣=1,先对式(2)中的协方差矩阵 M M M进行特征值分解,求得 M M M的各特征值, M M M的最小特征值所对应的特征向量即 P P P的法向量。
M = 1 k ∑ i = 1 k ( p i − p 0 ) ( p i − p 0 ) T (2) M=\frac{1}{k}\sum_{i=1}^k\ ( p_i-p_0)( p_i-p_0)^T\tag{2} M=k1i=1∑k (pi−p0)(pi−p0)T(2)
2、法向量定向
前面计算出的法向量具有二义性,即只是得到了法向量所在的直线,而没有确定以直线的那个方向为法向量的最终方向。用以下方法对求出的法向量进行重定向:
假设点云足够稠密且采样平面处处光滑,那么相邻两点的法向量会接近于平行。令 n i ⃗ 、 n j ⃗ \vec{n_i}、\vec{n_j} ni、nj为相邻两点 x i 、 x j {x_i}、{x_j} xi、xj的法向量,如果法向量的方向是一致的,那么 n i ⃗ ⋅ n j ⃗ ≈ 1 \vec{n_i}\cdot\vec{n_j}\approx1 ni⋅nj≈1若此内积为负,则说明其中某个点的法向量需要被翻转。因此,首先为点云中某个点设定一个法向量朝向,然后遍历其他所有点,若当前点法向量设定为 n i ⃗ , n j ⃗ \vec{n_i},\vec{n_j} ni,nj为下一个要遍历的点,如果 n i ⃗ ⋅ n j ⃗ < 0 \vec{n_i}\cdot\vec{n_j}<0 ni⋅nj<0则将 n j ⃗ \vec{n_j} nj翻转,否则保持不变。
3、表面曲率
对式(2)中的协方差矩阵 M M M进行特征值分解,求得 M M M的各特征值,若特征值满足 λ 0 ≤ λ 1 ≤ λ 2 \lambda_0\leq\lambda_1\leq\lambda_2 λ0≤λ1≤λ2,则 P P P点的表面曲率为:
δ = λ 0 λ 0 + λ 1 + λ 2 (3) \delta=\frac{\lambda_0}{\lambda_0+\lambda_1+\lambda_2}\tag{3} δ=λ0+λ1+λ2λ0(3)
δ \delta δ越小表明邻域越平坦, δ \delta δ越大则表明邻域的起伏变化越大。
4、参考文献
[1]王飞,刘如飞,任红伟,柴永宁.利用道路目标特征的多期车载激光点云配准[J].测绘科学技术学报,2020,37(05):496-502.
[2]邢正全,邓喀中,薛继群.基于K-近邻搜索的点云初始配准[J].测绘科学,2013,38(02):93-95.
[3]李新春,闫振宇,林森,贾迪.基于邻域特征点提取和匹配的点云配准[J].光子学报,2020,49(04):255-265.
5、法向量定向的理解
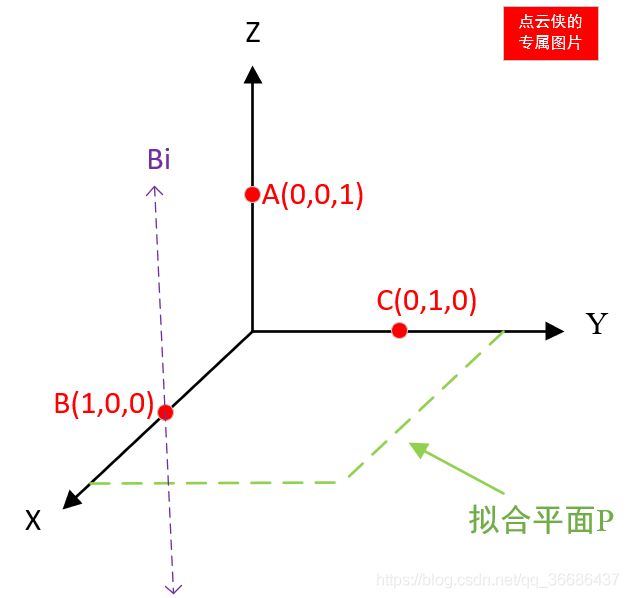
A , B , C A,B,C A,B,C表示坐标值, A i , B i , C I A_i,B_i,C_I Ai,Bi,CI表示向量,以 O A → \overrightarrow{OA} OA 作为正方向,由于 A A A点法向量已经定向,所以 A A A点法向量为: A i → \overrightarrow{A_i} Ai=(0,0,1),对 B B B点的法向量进行法向量方向的确定:
其中, B B B点的法向量坐标为: B i 1 → = ( 1 2 , 0 , 1 2 ) \overrightarrow{B_{i1}}=(\frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}}) Bi1=(21,0,21), B i 2 → = ( 1 2 , 0 , − 1 2 ) \overrightarrow{B_{i2}}=(\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}}) Bi2=(21,0,−21);(可以看出 B i → \overrightarrow{B_i} Bi 的方向与 O A → \overrightarrow{OA} OA 同向,定向的目的就是找出与 O A → \overrightarrow{OA} OA同向的 B i → \overrightarrow{B_i} Bi ),其理论依据为:
A i → ⋅ B i → > 0 (4) \overrightarrow{A_i}\cdot \overrightarrow{B_i}>0\tag{4} Ai⋅Bi>0(4)
所谓的调整方向就是:上式中计算,你带入的 B i → \overrightarrow{B_i} Bi 值为 B i 2 → \overrightarrow{B_{i2}} Bi2时,对 B i 2 → \overrightarrow{B_{i2}} Bi2进行操作使 B i 2 → \overrightarrow{B_{i2}} Bi2= B i 1 → \overrightarrow{B_{i1}} Bi1。
实际操作中,以 A A A点作为视点,求出: B i → ⋅ ( A − B ) > 0 \overrightarrow{B_i}\cdot \ (A-B)>0 Bi⋅ (A−B)>0时的 B i → \overrightarrow{B_i} Bi即为 B B B点与视点 A A A同向的法向量。
综上所述:所谓的定向就是以其中一点 N i N_i Ni的法向量方向作为正方向,其邻域内所有点的法向量 N j N_j Nj满足:
N j ⋅ N i > 0 (5) {N_j}\cdot {N_i}>0\tag{5} Nj⋅Ni>0(5)
6、CloudCompare
CloudCompare软件中也有计算法向量的功能,这里给出具体操作。
Normals > Compute:计算所选实体的法线
Normals > Invert:反转所选实体的法线
Normals > Orient Normals > With Minimum Spanning Tree:用同样的方法重新定位点云的全部法线(最小生成树)
Normals > Orient Normals > With Fast Marching:用同样的方法重新定位点云的全部法线(快速行进法)
Normals > Convert to > HSV:将云的法线转换到 HSV 颜色字段
Normals > Convert to > Dip and Dip direction SFs:转换点云的法线到两个标量域
Normals > Clear:为选定的实体移除法线
二、pcl::Normal的定义
compute(*normal)里计算出来的结果是:法向量的x,y,z坐标和表面曲率curvature。其内部结构为:
/*brief A point structure representing normal coordinates and the surface curvature estimate. (SSE friendly)ingroup common*/
struct Normal : public _Normal
{
inline Normal (const _Normal &p)
{
normal_x = p.normal_x;
normal_y = p.normal_y;
normal_z = p.normal_z;
data_n[3] = 0.0f;
curvature = p.curvature;
}
inline Normal ()
{
normal_x = normal_y = normal_z = data_n[3] = 0.0f;
curvature = 0;
}
inline Normal (float n_x, float n_y, float n_z)
{
normal_x = n_x; normal_y = n_y; normal_z = n_z;
curvature = 0;
data_n[3] = 0.0f;
}
friend std::ostream& operator << (std::ostream& os, const Normal& p);
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
};
三、pcl::Normal的几种输出方式
cout<<normals->points[0]<<endl;
cout<<"["<<normals->points[0].normal_x<<" "
<<normals->points[0].normal_y<<" "
<<normals->points[0].normal_z<<" "
<<normals->points[0].curvature<<"]"<<endl;
cout<<"["<<normals->points[0].normal[0]<<" "
<<normals->points[0].normal[1]<<" "
<<normals->points[0].normal[2]<<" "
<<normals->points[0].curvature<<"]"<<endl;
cout<<"["<<normals->points[0].data_n[0]<<" "
<<normals->points[0].data_n[1]<<" "
<<normals->points[0].data_n[2]<<" "
<<normals->points[0].curvature<<"]"<<endl;
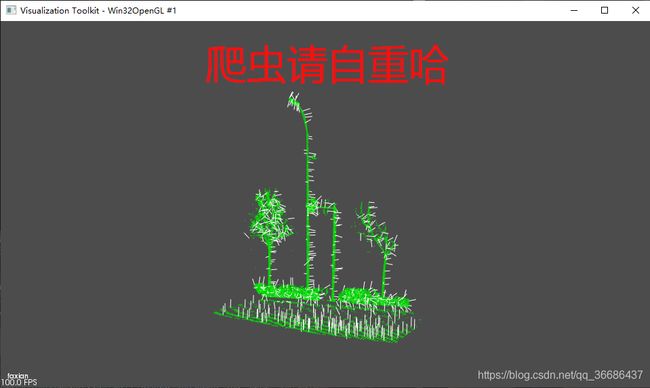
四、计算法线并显示
1、代码图解
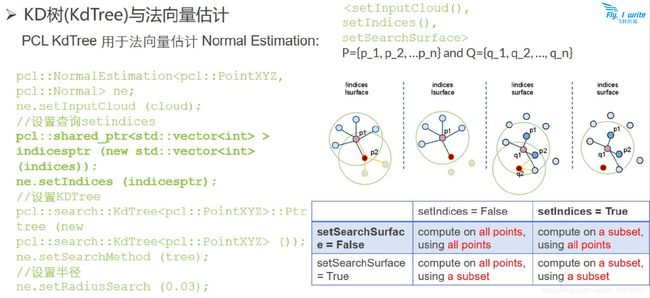
2、计算输入点云的所有点的法线
#include 3、计算输入点云数据中一个子集的法线
#include 4、特殊操作
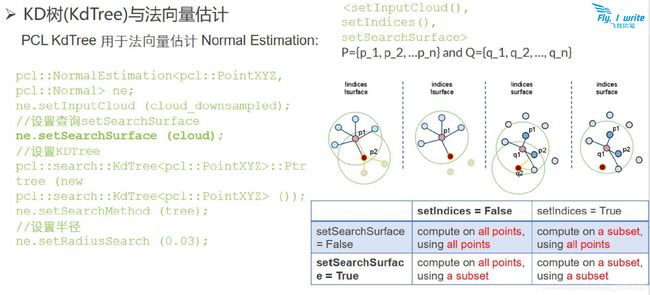
使用另一个数据集(该数据集比较完整)估计其最近邻近点,估算输入数据集(比较稀疏)中所有点的一组曲面法线。该方法适用于(类似)下采样后的点云。
#include 五、使用OMP的报错处理
在应用OpenMP,可能会报错“User Error 1001: argument to num_threads clause must be positive”。这是由于设置的线程数必须为正,而程序中可能没有设置,有时候甚至环境变量中设置了,但是依然报错,手动设置如下:
n.setNumberOfThreads(4); // 手动设置线程数,比源码增加,否则提示错误