视觉惯性融合学习笔记二 VI_ORB初始化方法

这篇笔记会记录论文里的关于初始化的方法，以及自己的一些心得，欢迎交流(´▽‘)ﾉ。

一、概述

视觉惯性融合导航系统（VINS）因为相机和IMU的互补特性而被关注，但性能提升的前提是能够获取好的初始值。好的初始值能提高定位准确性，帮助系统收敛；而坏的初始值甚至会降低系统的性能。目前来说，VINS系统增加的初始化内容包括：尺度s、重力向量$g_w$，速度v，陀螺仪偏置$b_g$、加速度计偏置$b_a$、相机和IMU之间的外参$T_{CB}=[R_{CB}{|}_c^{}{\text{p}}_B]$（一般默认已知）。

二、VI_ORB初始化方法

方法来源：Raul Mur-Artal在2017年发表的论文Visual-Inertial Monocular SLAM With Map Reuse。Raul在论文里把初始化问题分成4步来解决：（1）陀螺仪偏置估计；（2）绝对尺度和重力粗估计；（3）加速度计偏置估计，细化尺度和重力；（4）速度估计。其中会使用预积分理论，有需要可以参考我整理的笔记视觉惯性融合学习笔记一 预积分理论。

2.1 VI_ORB初始阶段简述

在初始阶段VI_ORB会先运行纯ORBSLAM一段时间，通过优化参数初始值使残差（目标函数）最小。
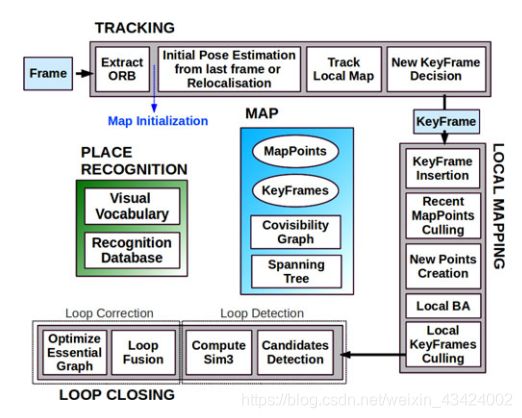
纯ORBSLAM有3个并行线程，tracking线程对关键帧之间的每个相机帧提取特征，匹配局部地图点，优化关键帧之间所有相机帧的重投影误差，并不断估计当前相机帧的位姿，直到局部地图点更新；local mapping线程负责管理地图点和关键帧，当检测到新的关键帧时，会开启局部BA，优化前N个关键帧位姿和这些帧看到的所有的地图点；loop closing线程通过place recognition模块将当前关键帧与过去的关键帧匹配，并优化位姿图。
这里引用ORBSLAM论文里的图，图片显示的是ORBSLAM的系统结构。

2.2 陀螺仪偏置估计

当ORBSLAM检测到N个关键帧时，先进行陀螺仪偏置估计。方法是以连续两个关键帧的ORBSLAM姿态估计值和IMU预积分的残差作为目标函数进行优化。
对于连续两帧关键帧i和i+1，关键帧i的ORBSLAM估计姿态记为$R_{WC}^i$，关键帧i+1的估计姿态记为$R_{WC}^{i+1}$，相机坐标系到体坐标系间的旋转矩阵为$R_{CB}$。假设在初始化阶段，陀螺仪偏置存在小扰动，但是可以忽略，仍旧认为其为常数，两个关键帧之间的IMU预积分姿态测量值为（这里忽略了陀螺仪的测量噪声）：
$$\Delta R_{ii+1}=Exp[({\omega }_i-b^g)\Delta t]$$
其中${\omega }_i$表示关键帧i的陀螺仪测量值；$b^g$表示关键帧i的陀螺仪偏置，是待优化的量。
可以建立目标函数：
$$\underset{b^g}{\mathrm{argmin}}\sum _{i=1}^{N-1}||log[(\Delta R_{ii+1}Exp(J_{\Delta R}^g{b}^g){)}^T]R_{BW}^{i+1}{R}_{WB}^i|{|}^2$$
其中$J_{\Delta R}^g=\frac{\partial \Delta R_{ii+1}}{\partial b^g}$，因为假设了扰动，所以这个Jacobian的计算是有意义的；$R_{WB}^{i+1}=R_{WC}^{i+1}{R}_{CB}$表示世界坐标系到关键帧i+1对应的体坐标系的旋转矩阵；$R_{WB}^i=R_{WC}^i{R}_{CB}$表示关键帧i对应的IMU姿态。
令初始陀螺仪偏置为0，直接用Gauss-Newton法进行优化可以估计陀螺仪偏置初始值。

2.3 绝对尺度和重力粗估计

在估计陀螺仪偏置之后，关键帧i对应的IMU姿态测量值变成$R_{WB}^i$已知。这时可以通过其他两个IMU预积分测量值估计绝对尺度和重力。
和陀螺仪偏置估计的方式不同，由于陀螺仪偏置已知，这里先忽略加速度计偏置和噪声的影响，因此可以计算出IMU位置和速度预积分测量值。利用已经计算的IMU预积分测量值，可以求得关键帧i+1的IMU位置测量值和速度测量值：
$$p_{i+1}=p_i+v_i\Delta t_{ii+1}+\frac{1}{2}{g}^W\Delta t_{ii+1}^2+R_{WB}^i\Delta p_{ii+1}$$$$v_{i+1}=v_i+g^W\Delta t_{ii+1}+R_{WB}^i\Delta v_{ii+1}$$
其中$p_i$和$p_{i+1}$分别表示关键帧i和i+1对应的IMU在世界坐标系的位置；$v_{i+1}$和$v_i$分别表示关键帧i+1和i对应的IMU的速度；$\Delta t_{ii+1}$为两帧之间的时间差；$g^W$表示重力加速度向量；$R_{WB}^i$表示关键帧i对应的IMU姿态；$\Delta p_{ii+1}$表示IMU预积分位置测量值；$\Delta v_{ii+1}$表示IMU预积分速度测量值。
将上式的IMU在世界坐标系的位置$p_i$和$p_{i+1}$转换为相机在世界坐标系的位置${}_W^{}{\text{p}}_c^i$和${}_W^{}{\text{p}}_c^{i+1}$后得到：
$$s_W^{}{\text{p}}_c^{i+1}=s_W^{}{\text{p}}_c^i+v_i\Delta t_{ii+1}+\frac{1}{2}{g}^W\Delta t_{ii+1}^2+R_{WB}^i\Delta p_{ii+1}+(R_{WC}^i-R_{WC}^{i+1}{)}_c^{}{\text{p}}_B$$
为了利用避免出现IMU速度测量值，考虑连续3帧关键帧，分别将${}_W^{}{\text{p}}_c^{i+1}$乘以$\Delta t_{i+1i+2}$，${}_W^{}{\text{p}}_c^{i+1}$乘以$\Delta t_{ii+1}$后计算差值，可以得到方程，用矩阵表示为：
$$[\lambda (i)\beta (i)]\left[\begin{array}{c}s\\ g^W\end{array}\right]=\gamma (i)$$
用1,2,3简单表示i,i+1,i+2，得到
$$\lambda (i)={(}_W^{}{\text{p}}_c^2{-}_W^{}{\text{p}}_c^1)\Delta t_{23}-{(}_W^{}{\text{p}}_c^3{-}_W^{}{\text{p}}_c^2)\Delta t_{12}$$$$\beta (i)=\frac{1}{2}{I}_{3\times 3}(\Delta t_{12}^2\Delta t_{23}+\Delta t_{23}^2\Delta t_{12})$$$$\gamma (i)=(R_{WC}^2-R_{WC}^1{)}_c^{}{\text{p}}_B\Delta t_{23}-(R_{WC}^3-R_{WC}^2{)}_c^{}{\text{p}}_B\Delta t_{12}+$$$$R_{WB}^2\Delta p_{23}\Delta t_{12}-R_{WB}^1\Delta p_{12}\Delta t_{23}+R_{WB}^1\Delta v_{12}\Delta t_{12}\Delta t_{23}$$
但是我作差的结果和论文结果有差异，我计算的结果是
$$[\lambda (i)\beta (i)]\left[\begin{array}{c}s\\ g^W\end{array}\right]=-\gamma (i)$$
因为我还没有实现过论文里的方法，目前仍然存疑。
之后利用奇异值分解（SVD）可以得到尺度和重力向量的初步估计值。

2.4 加速度计偏置估计，细化尺度和重力

先避免计算加速度计偏置，是因为加速度计偏置远小于重力，很难与重力区分，这里利用重力大小G和惯性坐标系I下的重力方向${\hat{g}}_I=[0,0,-1]$帮助估计。设2.3估计的重力初始值为$g_W^{\ast }$，则对应的重力方向为${\hat{g}}_W=g_W^{\ast }/||g_W^{\ast }||$。
计算从惯性系I到世界坐标系的旋转矩阵为：
$$R_{WI}=Exp(\hat{v}\theta )$$$$\hat{v}=\frac{{\hat{g}}_I\times {\hat{g}}_W}{||{\hat{g}}_I\times {\hat{g}}_W||}I$$$$\theta =atan2(||{\hat{g}}_I\times {\hat{g}}_W||,{\hat{g}}_I\cdot {\hat{g}}_W)$$
其中$\hat{v}$为从I系到W系的旋转轴；$\theta$为从I系到W系的旋转角；$R_{WI}$为为从I系到W系的旋转矩阵。
设给$R_{WI}$施加一个小扰动$Exp(\delta \theta )$，因为绕z轴上的扰动不会对重力产生影响，因此$\delta \theta =[\delta {\theta }_{xy}^T,0]$，$\delta {\theta }_{xy}=[\delta {\theta }_x,\delta {\theta }_y]$。这样估计W系下的重力向量可以转化为估计I系到W系的旋转矩阵：
$$g_W=R_{WI}{\hat{g}}_{I}G-R_{WI}{\lfloor g_I\rfloor }_{\times }G\delta \theta$$
将重力向量$g_W$代入关键帧i+1的IMU位置测量值：
$$s_W^{}{\text{p}}_c^{i+1}=s_W^{}{\text{p}}_c^i+v_i\Delta t_{ii+1}+\frac{1}{2}{R}_{WI}{\hat{g}}_{I}G\Delta t_{ii+1}^2-\frac{1}{2}{R}_{WI}{\lfloor g_I\rfloor }_{\times }G\delta \theta \Delta t_{ii+1}^2+$$$$R_{WB}^i\Delta p_{ii+1}+(R_{WC}^i-R_{WC}^{i+1}{)}_c^{}{\text{p}}_B$$
对连续3帧关键帧，考虑加速度计偏置变化时的预积分修正，可以得到方程：
$$[\lambda (i)\varphi (i)\zeta (i)]\left[\begin{array}{c}s\\ \delta {\theta }_{xy}\\ b_a\end{array}\right]=\psi (i)$$
用1,2,3简单表示i,i+1,i+2：
$$\varphi (i)=[\frac{1}{2}{R}_{WI}{\lfloor g_I\rfloor }_{\times }G(\Delta t_{12}^2\Delta t_{23}+\Delta t_{23}^2\Delta t_{12}){]}_{(:,1:2)}$$$$\zeta (i)=R_{WB}^2{J}_{\Delta p_{23}}^a\Delta t_{12}-R_{WB}^1{J}_{\Delta p_{12}}^a\Delta t_{23}+R_{WB}^1{J}_{\Delta v_{23}}^a\Delta t_{12}\Delta t_{23}$$
$$\psi (i)=(R_{WC}^2-R_{WC}^1{)}_c^{}{\text{p}}_B\Delta t_{23}-(R_{WC}^3-R_{WC}^2{)}_c^{}{\text{p}}_B\Delta t_{12}+$$$$R_{WB}^2\Delta p_{23}\Delta t_{12}-R_{WB}^1\Delta p_{12}\Delta t_{23}+R_{WB}^1\Delta v_{12}\Delta t_{12}\Delta t_{23}+$$$$\frac{1}{2}{R}_{WI}{\hat{g}}_{I}G(\Delta t_{12}^2\Delta t_{23}+\Delta t_{23}^2\Delta t_{12})$$
这里我推导的结果和论文也有一些出入，除了上面修改的$\psi (i)$的最后一项外，我计算的方程为：
$$[\lambda (i)-\varphi (i)\zeta (i)]\left[\begin{array}{c}s\\ \delta {\theta }_{xy}\\ b_a\end{array}\right]=-\psi (i)$$
还没有实现过论文里的方法，这里目前也仍然存疑。
同样利用SVD可以求解方程。

2.5 速度估计

在已经求出陀螺仪偏置、尺度、重力、加速度计偏置的情况下，速度初值是可以直接计算的：
$$v_{i+1}=v_i+g^W\Delta t_{ii+1}+R_{WB}^i(\Delta v_{ii+1}+J_{\Delta v_{ii+1}}^g{b}_g+J_{\Delta v_{ii+1}}^a{b}_a)$$
这里计算的速度是最靠近当前帧的关键帧对应的IMU速度。

到这里VI_ORB的初始化过程就结束了，虽然从公式上看好像很清楚，但是感觉实现起来不会简单；上面的内容有一些是自己的推测，也有一些与论文有出入，大家有想法的话，欢迎交流≧∀≦)o)。