算法导论 — 8.4 桶排序
笔记
为简化对于桶排序的分析,我们假设 n n n个输入数据分布在 [ 0 , 1 ) [0, 1) [0,1)区间上。将 [ 0 , 1 ) [0, 1) [0,1)区间划分为 n n n个相同大小的子区间,这些子区间都称为桶。如果输入数据是均匀分布的,可以预见每个桶所包含的元素个数是近乎均匀的,不太可能出现很多元素都落在同一个桶中的情况。为得到输出,我们先对每个桶中的元素进行排序,然按照次序把每个桶中的元素列出来即可。
在下面桶排序的伪代码中,输入是一个包含 n n n个元素的数组 A A A,且每个元素 A [ i ] A[i] A[i]满足 0 ≤ A [ i ] < 1 0 ≤ A[i] < 1 0≤A[i]<1。此外,还需要一个临时数组 B [ 0.. n − 1 ] B[0..n−1] B[0..n−1]来存放桶,这里的桶实际上是链表。另外,对每个桶内元素的排序采用的是插入排序算法。实际上由于每个桶都是一个链表,故采用插入排序是可行的,采用快速排序、堆排序等其他排序算法反而不可行。

下面给出一个例子来展示桶排序算法的过程。
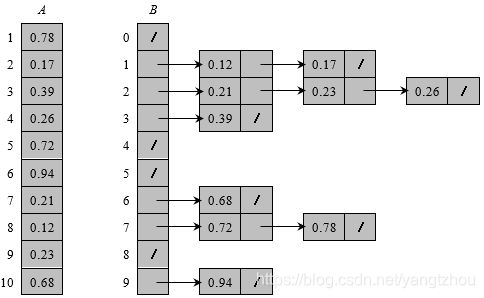
在桶排序算法中,除了第 8 8 8行以外,所有其他各行的时间代价都是 Θ ( n ) Θ(n) Θ(n)。我们现在来分析桶排序算法的期望运行时间。
用随机变量 n i n_i ni表示桶 B [ i ] B[i] B[i]中的元素个数,于是可以得到桶排序的运行时间为
T ( n ) = Θ ( n ) + ∑ i = 0 n − 1 O ( n i 2 ) T(n)=Θ(n)+\sum\limits_{i=0}^{n-1}O(n_i^2 ) T(n)=Θ(n)+i=0∑n−1O(ni2)
对上式取期望,得到
E [ T ( n ) ] = E [ Θ ( n ) + ∑ i = 0 n − 1 O ( n i 2 ) ] = Θ ( n ) + ∑ i = 0 n − 1 E [ O ( n i 2 ) ] E[T(n)]=E[Θ(n)+\sum\limits_{i=0}^{n-1}O(n_i^2 ) ]=Θ(n)+\sum\limits_{i=0}^{n-1}E[O(n_i^2 )] E[T(n)]=E[Θ(n)+i=0∑n−1O(ni2)]=Θ(n)+i=0∑n−1E[O(ni2)]
我们先单独分析 ∑ i = 0 n − 1 E [ O ( n i 2 ) ] \sum_{i=0}^{n-1}E[O(n_i^2 )] ∑i=0n−1E[O(ni2)]这一项,令 T ′ = ∑ i = 0 n − 1 E [ O ( n i 2 ) ] T'=\sum_{i=0}^{n-1}E[O(n_i^2 )] T′=∑i=0n−1E[O(ni2)]。根据 O O O记号的定义,存在正常量 c c c,使得对于足够大的 n i n_i ni,有 T ′ ≤ ∑ i = 0 n − 1 E [ c n i 2 ] = ∑ i = 0 n − 1 c E [ n i 2 ] T'≤\sum_{i=0}^{n-1}E[cn_i^2 ] =\sum_{i=0}^{n-1}cE[n_i^2 ] T′≤∑i=0n−1E[cni2]=∑i=0n−1cE[ni2] 。于是有 T ′ = ∑ i = 0 n − 1 O ( E [ n i 2 ] ) T'=\sum_{i=0}^{n-1}O(E[n_i^2 ]) T′=∑i=0n−1O(E[ni2])。于是 E [ T ( n ) ] E[T(n)] E[T(n)]可以写为
E [ T ( n ) ] = Θ ( n ) + ∑ i = 0 n − 1 O ( E [ n i 2 ] ) E[T(n)]=Θ(n)+\sum\limits_{i=0}^{n-1}O(E[n_i^2 ]) E[T(n)]=Θ(n)+i=0∑n−1O(E[ni2])
我们现在来分析 E [ n i 2 ] E[n_i^2 ] E[ni2]。对所有 i = 0 , 1 , … , n − 1 i = 0, 1, …, n−1 i=0,1,…,n−1和 j = 1 , 2 , … , n j = 1, 2, …, n j=1,2,…,n,定义指示器随机变量 X i j X_{ij} Xij
X i j = I { A [ j ] 落 入 桶 B [ i ] 中 } X_{ij} = I\{A[j]落入桶B[i]中\} Xij=I{ A[j]落入桶B[i]中}
于是可以得到桶 i i i中的元素个数 n i = ∑ j = 1 n X i j n_i=\sum\limits_{j=1}^{n}X_{ij} ni=j=1∑nXij。于是有
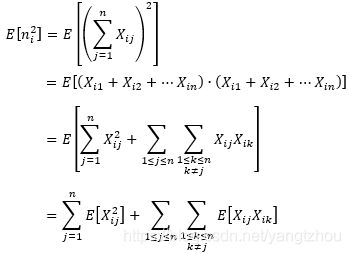
现在分别计算这两项累加和。由于我们假定输入数据服从均匀分布,所以指示器随机变量 X i j X_{ij} Xij为 1 1 1的概率是 1 / n 1/n 1/n,为 0 0 0的概率是 1 − 1 / n 1−1/n 1−1/n。于是有
E [ X i j 2 ] = 1 2 ∙ 1 n + 0 2 ∙ ( 1 − 1 n ) = 1 n E[X_{ij}^2 ]=1^2∙\frac{1}{n}+0^2∙(1-\frac{1}{n})=\frac{1}{n} E[Xij2]=12∙n1+02∙(1−n1)=n1
当 k ≠ j k ≠ j k=j时,随机变量 X i j X_{ij} Xij和 X i k X_{ik} Xik是互相独立的,因此有
E [ X i j X i k ] = E [ X i j ] E [ X i k ] = 1 n ∙ 1 n = 1 n 2 E[X_{ij}X_{ik}]=E[X_{ij}]E[X_{ik}]=\frac{1}{n}∙\frac{1}{n}=\frac{1}{n^2} E[XijXik]=E[Xij]E[Xik]=n1∙n1=n21
利用这两个期望值可以得到
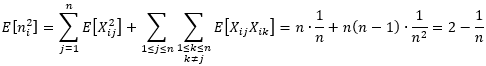
最终可以得到桶排序算法的期望运行时间为
E [ T ( n ) ] = Θ ( n ) + ∑ i = 0 n − 1 O ( E [ n i 2 ] ) = Θ ( n ) + n ∙ O ( 2 − 1 n ) = Θ ( n ) E[T(n)]=Θ(n)+\sum\limits_{i=0}^{n-1}O(E[n_i^2 ]) =Θ(n)+n∙O(2-\frac{1}{n})=Θ(n) E[T(n)]=Θ(n)+i=0∑n−1O(E[ni2])=Θ(n)+n∙O(2−n1)=Θ(n)
根据以上分析,如果输入数据服从均匀分布,桶排序可以在线性时间内完成。然而,根据等式 E [ T ( n ) ] = Θ ( n ) + ∑ i = 0 n − 1 O ( E [ n i 2 ] ) E[T(n)]=Θ(n)+\sum_{i=0}^{n-1}O(E[n_i^2 ]) E[T(n)]=Θ(n)+∑i=0n−1O(E[ni2]),只要满足所有桶中元素个数 n 0 , n 1 , … n n − 1 n_0, n_1, …n_{n−1} n0,n1,…nn−1的平方和 ∑ i = 0 n − 1 n i 2 = Θ ( n ) \sum_{i=0}^{n-1}n_i^2 =Θ(n) ∑i=0n−1ni2=Θ(n),桶排序就仍然可以在线性时间内完成。
练习
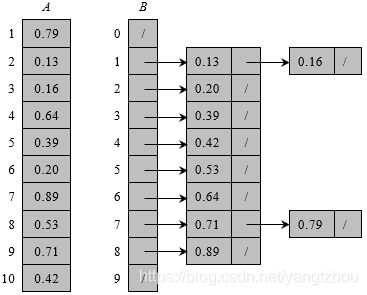
8.4-1 参照图8-4的方法,说明BUCKET-SORT在数组 A = < 0.79 , 0.13 , 0.16 , 0.64 , 0.39 , 0.20 , 0.89 , 0.53 , 0.71 , 0.42 > A = <0.79, 0.13, 0.16, 0.64, 0.39, 0.20, 0.89, 0.53, 0.71, 0.42> A=<0.79,0.13,0.16,0.64,0.39,0.20,0.89,0.53,0.71,0.42>上的操作过程。
解
8.4-2 解释为什么桶排序在最坏情况下运行时间是 Θ ( n 2 ) Θ(n^2) Θ(n2)?我们应该如何修改算法,使其在保持平均情况为线性时间代价的同时,最坏情况下时间代价为 Θ ( n l g n ) Θ(n{\rm lgn}) Θ(nlgn)?
解
桶排序的最坏情况发生在所有元素都集中一个桶中的时候,这时候对桶内的元素调用插入排序的时间为 Θ ( n 2 ) Θ(n^2) Θ(n2)。
要使得桶排序最坏情况下的时间代价为 Θ ( n l g n ) Θ(n\rm{lg}n) Θ(nlgn),可以将桶内元素的插入排序算法替换为具有 O ( n l g n ) O(n{\rm lg}n) O(nlgn)时间复杂度的排序算法。然而每个桶都是一个链表,符合 O ( n l g n ) O(n{\rm lg}n) O(nlgn)时间复杂度并且适合链表的排序算法只有归并排序。堆排序虽然时间复杂度也为 O ( n l g n ) O(n{\rm lg}n) O(nlgn),但是不能应用在链表上。
8.4-3 设 X X X是一个随机变量,用于表示在将一枚硬币抛掷两次时,正面朝上的次数。 E [ X 2 ] E[X^2] E[X2]是多少呢? E 2 [ X ] E^2[X] E2[X]是多少呢?
解
下表列出了 X X X可能的取值以及概率。
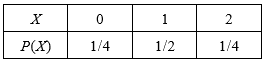
于是有
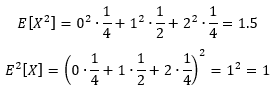
8.4-4 在单位圆内给定 n n n个点, p i = ( x i , y i ) p_i = (x_i, y_i) pi=(xi,yi),对所有 i = 1 , 2 , … , n i = 1, 2, …, n i=1,2,…,n,有 0 < x i 2 + y i 2 ≤ 1 0
解
可以按照面积将圆等分为 n n n等份。由于排序是按照点到圆心的距离来进行的,所以可以用同心圆来将圆进行 n n n等分,如下图所示。
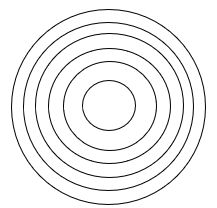
等分的目标是使得相邻同心圆之间的区域的面积相等。单位圆的面积 S = π ∙ 1 2 = π S = π∙1^2 = π S=π∙12=π。 n n n等分之后,每个区域的面积 s = π / n s = π/n s=π/n。可以算得同心圆的半径分别为 r 1 = 1 / n , r 2 = 2 / n , … , r n = n / n r_1=\sqrt{1/n}, r_2=\sqrt{2/n}, …, r_n=\sqrt{n/n} r1=1/n,r2=2/n,…,rn=n/n。对于第 i i i个等分区域,它内部的点到圆心的距离在 ( r i − 1 , r i ] (r_{i-1}, r_i] (ri−1,ri]之中 (注意: r 0 = 0 r_0 = 0 r0=0)。于是,我们对单位圆内的 n n n个点进行桶排序,具体做法是将到圆心距离在 ( r i − 1 , r i ] (r_{i-1}, r_i] (ri−1,ri]之内的点放入第 i i i个桶中。
如果按照距离来将每个点放入相应的桶中,还需要根据距离来查找相应的区间,而并不能直接将点入桶。这是因为在划分区间时,是按面积等分,而不是按距离等分。对每个点来说,用二分查找法来查找区间所花费的时间为 O ( l g n ) O({\rm lg}n) O(lgn),这样一来桶排序算法的代价为 O ( n l g n ) O(n{\rm lg}n) O(nlgn)。而如果利用面积作为参考,可以在 Θ ( 1 ) Θ(1) Θ(1)时间内将一个点放入到相应的桶中。对于点 ( x i , y i ) (x_i, y_i) (xi,yi)来说,经过该点的同心圆的面积 A i = π ( x i 2 + y i 2 ) A_i=π(x_i^2+y_i^2 ) Ai=π(xi2+yi2),那么这个点应当放入第 ⌈ A i / s ⌉ = ⌈ n ( x i 2 + y i 2 ) ⌉ ⌈A_i/s⌉=⌈n(x_i^2+y_i^2 )⌉ ⌈Ai/s⌉=⌈n(xi2+yi2)⌉个桶中 (注意,这里桶的序号从 1 1 1开始,而不是从 0 0 0开始)。
以下是该算法的伪代码。

8.4-5 定义随机变量 X X X的概率分布函数 P ( x ) P(x) P(x)为 P ( x ) = P r { X ≤ x } P(x) = Pr\{X ≤ x\} P(x)=Pr{ X≤x}。假设有 n n n个随机变量 X 1 , X 2 , … , X n X_1, X_2, …, X_n X1,X2,…,Xn服从一个连续概率分布函数 P P P,且它可以在 O ( 1 ) O(1) O(1)时间内被计算得到。设计一个算法,使其能够在平均情况下在线性时间内完成这些数的排序。
解
根据概率分布函数 P ( x ) P(x) P(x)将随机变量 X 1 , X 2 , … , X n X_1, X_2, …, X_n X1,X2,…,Xn划分到 n n n个桶内。对于任意一个随机变量 X i X_i Xi,将其放入第 ⌈ n P ( X [ i ] ) ⌉ ⌈nP(X[i])⌉ ⌈nP(X[i])⌉个桶 (注意,这里桶的序号从 1 1 1开始,而不是从 0 0 0开始)。如果 n n n个随机变量 X 1 , X 2 , … , X n X_1, X_2, …, X_n X1,X2,…,Xn服从概率分布函数 P ( x ) P(x) P(x),那么执行上述划分方法之后,所有随机变量应当会均匀分布在所有桶内。以下是伪代码。

代码链接:
https://github.com/yangtzhou2012/Introduction_to_Algorithms_3rd/tree/master/Chapter08/Section_8.4