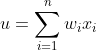《图解深度学习》学习笔记（一）

第一章 绪论

监督学习：需要基于输入数据及其期望输出，通过训练从数据中提取通用信息或特征信息(特征值)，以此得到预测模型。这里的特征值是指根据颜色和边缘等认为定义的提取方法从训练样本中提取的信息。（特征值就是根据图像转换成一串数值。）

以往的图像识别普遍使用尺度不变特征变换（Scale-Invariant Feature Transform,SIFT）、视觉词袋模型（Bag of Visual Words, BoVW)特征表达，以及费舍尔向量(Fishier Vector, FV)等尺度压缩方法。

GPU支持并行计算。计算力的提升和网络数据的采集，使得深度学习成为可能。

为什么是深度学习？

以往的机器学习都是人类手动设计特征值。例如在进行图像分类时，需要事先确定颜色、边缘或范围，再进行机器学习；

而深度学习则是通过学习大量数据自动确定需要提取的特征信息，甚至还能自动获取一些人类无法想象的由颜色和边缘等组合起来的特征信息。所以，利用深度学习，即便是难度较高的认证问题也能得到绝佳的性能。

什么是深度学习？

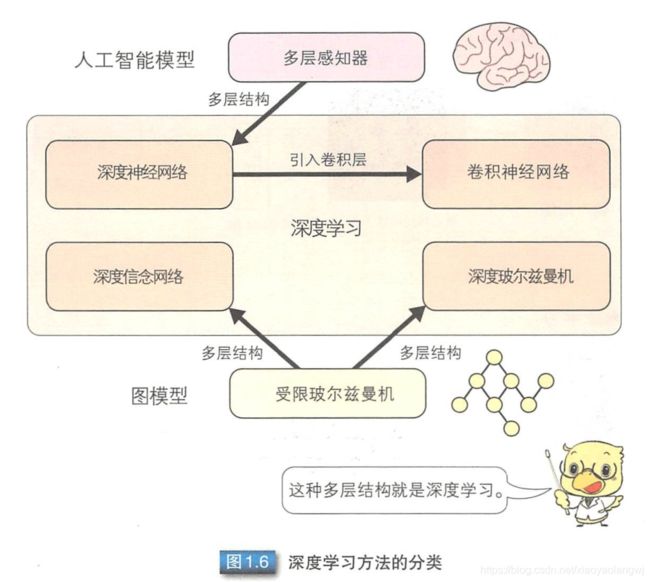
深度学习的起源包括感知器和玻尔兹曼机。

• 起源于“感知机”的深度学习中，最基本的结构是把多个感知器组合到一起得到的多层感知器。在多层感知器的基础上加入类似人类视觉皮质的结构而得到的卷积神经网络被广泛应用于图像识别领域。
• 起源于“基于图模型的玻尔兹曼机”的深度学习中，深度玻尔兹曼机以及深度信念网络是通过把多个受限玻尔兹曼机组合到一起而得到的。

起源于感知器的深度学习是一种有监督学习，根据期望输出训练网络；而起源于受限玻尔兹曼机的深度学习是一种无监督学习，只根据特定的训练数据训练网络。

第二章 神经网络

 

神经网络的历史

 

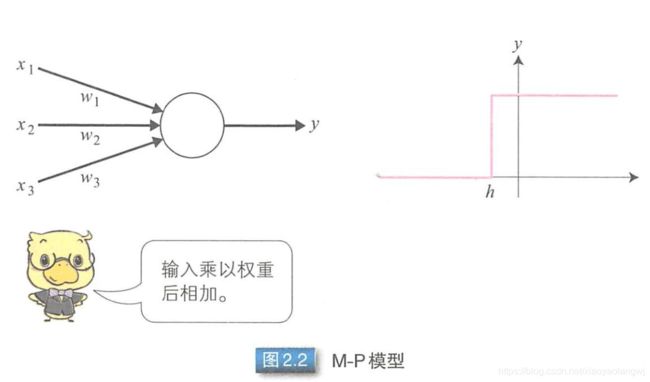
1、M-P模型：首个通过模仿神经元而形成的模型

在M-P模型中，多个输入节点{ }对应于一个输出节点y。每个输入乘以相应的连接权重wi,然后相加得到输出y。结果之和如果大于阈值h,则输出1，否则输出0。输入和输出均是0或1。

 

大于阈值输出1，否则为0。可以单入单出，也可以多入单出。

以or运算为例：y= f(x1+x2 -0.5)。x1和x2有一个为1，则输出1。

以and运算为例：y = f(x1+x2 -1.5)。x1和x2同时为1，则输出1。

人为事先计算后确定好权重系数。通过电阻来物理实现。可实现or和and操作。

---

2、感知器

与M-P模型需要人为确定参数不同，感知器能够通过训练自动确定参数。

训练方式为有监督学习，即需要设定训练样本和期望输出，然后调整实际输出和期望输出之差的方式（误差修正学习）。

h  h - α( r - y )

α是确定连接权重调整值的参数。a增大则误差修正速度增加，a减小则误差修正速度降低。学习率：用于控制调整速度，太大会影响训练的稳定性，太小则使训练的收敛速度变慢。

感知器中调整权重的基本思路如下：

• 实际输出y与期望输出 r 相等时，w和h不变。
• 实际输出y与期望输出 r 不相等时，调整w和h的值。

w和h的调整包括以下两种情况：

1）实际输出y=1、期望输出r=1时（未激活）

• 减小h

• 增大xi=1的连接权重wi

• xi=0的连接权重不变。

2）实际输出y=1、期望输出r =0时（激活过度）

• 增大h

• 降低xi=1的连接权重wi

• xi=0的连接权重不变。

 

因为感知器会利用随机数来初始化各项参数，所以训练得到的参数可能并不相同。

使用误差修正学习，我们可以自动获取参数，这是感知器引发的一场巨大变革。但是感知器训练只能解决线性可分问题，不能解决线性不可分问题。为了解决线性可分问题，我们需要使用多层感知机。

3、多层感知器

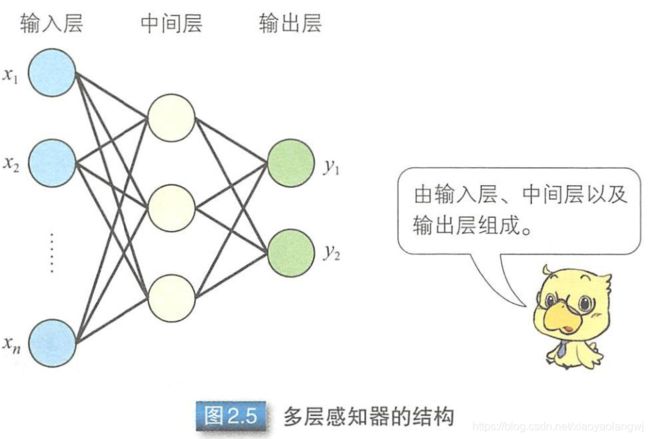
为了解决线性不可分等更复杂的问题，人们提出了多层感知器(multilayer perceptron)模型。

多层感知器指的是由多层结构的感知器递阶组成的输入值向前传播的网络，也被称为前馈网络或正向传播网络。

多层感知器通常采用三层结构，由输入层、中间层及输出层组成。与的M-P模型相同，中间层的感知器通过权重与输入层的各个单元（unit）相连接，通过阈值函数计算中间层各单元的输出值。中间层与输出层之间同样是通过权重相连接。

如何确定各层之间的连接权重呢？单层感知器是通过误差修正学习确定输入层与输出层之间的连接权重的。同样地，多层感知器也可以通过误差修正学习确定两层之间的连接权重。误差修正学习是根据输入数据的期望输出和实际输出之间的误差来调整连接权重，但是不能跨层调整，所以无法进行多层训练。因此，初期的多层感知器使用随机数确定输入层与中间层之间的连接权重，只对中间层与输出层之间的连接权重进行误差修正学习。所以，就会出现输入数据虽然不同，但是中间层的输出值却相同，以至于无法准确分类的情况。

那么，多层网络中应该如何训练连接权重呢？人们提出了误差反向传播算法。

4、误差反向传播算法

计算误差可以使用最小二乘误差函数。通过期望输出r和网络的实际输出y计算最小二乘误差函数E。E趋近于0，表示实际输出与期望输出更加接近。所以，多层感知器的训练过程就是不断调整连接权重w。以使最小二乘误差函数趋近于0。

误差反向传播算法是什么？

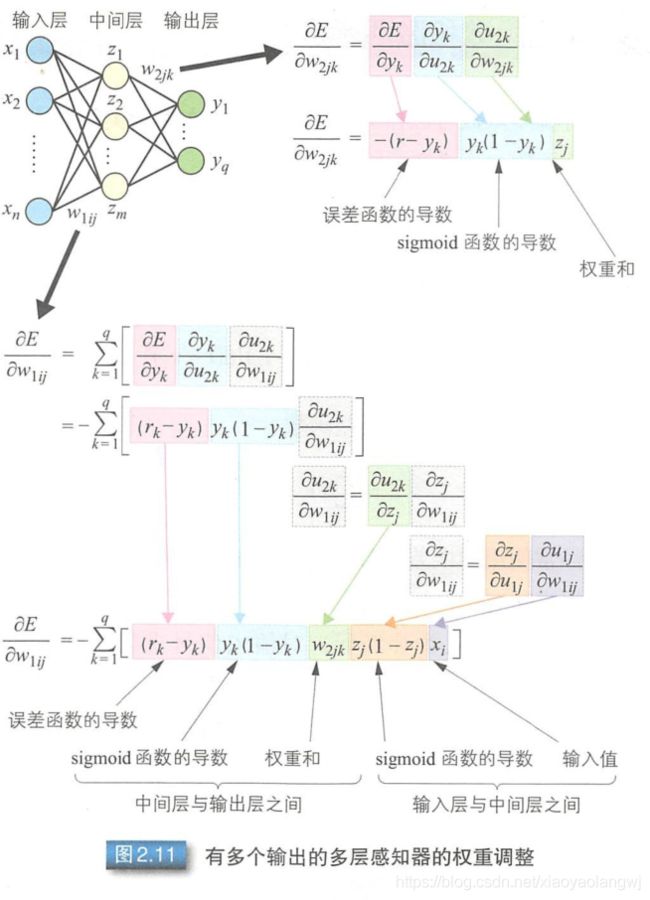
误差反向传播算法就是通过比较实际输出和期望输出得到误差信号，把误差信号从输出层逐层向前传播得到各层的误差信号，再通过调整各层的连接权重以减小误差。权重的调整主要使用梯度下降法。

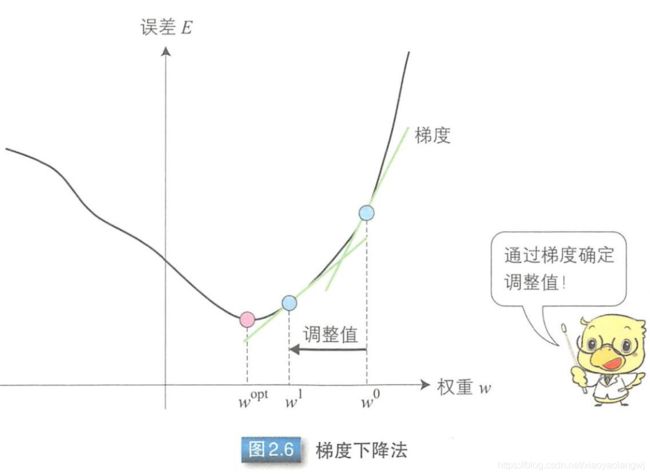
梯度下降法：通过实际输出和期望输出之间的误差E和梯度，确定连接权重w0的调整值，得到新的连接权重w1。然后像这样不断的调整权重以使误差达到最小，从中学习得到最优的连接权重wopt。

 

如何调节权重呢？

权重需要进行调整以使最小二乘误差函数趋近于0。对误差函数求导得到如图2.6中给定的梯度，即可在误差大时增大调整值，误差小时减小调整值，所以连接权重调整值可以用公式表示为：

     表示学习率，根据误差的程度进行权重调整。误差大，学习率大，误差小，学习率小。

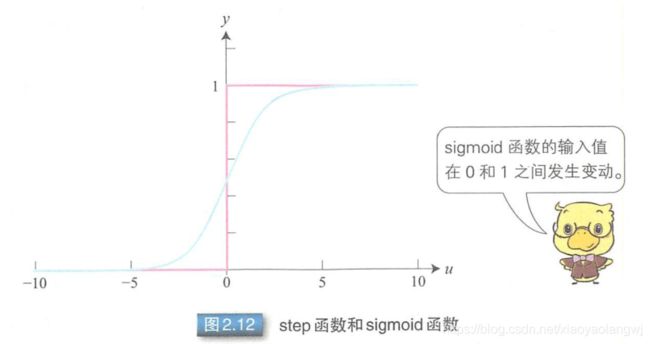
通过误差方向传播算法调整多层感知器的连接权重时，一个瓶颈问题是激活函数。M-P模型中使用step函数作为激活函数，只能输出0或者1，不连续，所以不可导。为了使误差能够传播，使用可导函数sigmoid作为激活函数。

权重调整值的计算就是对误差函数、激活函数以及连接权重 分别求导的过程。把得到的导数合并起来就得到了中间层与输出层之间的连接权重。而输入层与中间层之间的连接权重继承了上述误差函数和激活函数的导数。所以对连接权重求导就是对上一层的连接权重、中间层与输入层的激活函数以及连接权重进行求导的过程。像这种从后往前逐层求导的过程就称为链式法则（chain rule）。

输入层与与中间层之间的权重调整值是相关单元在中间层与输出层之间的权重调整值的总和。

梯度消失问题：

sigmoid函数：

                                                                 

激活函数使用sigmoid函数时，如果如果u远小于0，则y值趋近于0。所以，权重调整公式中对sigmoid函数求导后所得到的函数趋近于0。反之，如果u远大于1，则y值趋近于1，sigmoid函数求导后所得到的函数仍然趋近于0。此时由于权重调整值趋近于零，所以无法调整连接权重。这就是误差反向传播算法中的梯度消失导致无法调整连接权重的问题。对于这个问题，需要在训练过程中，调整学习率以防止梯度消失。

---

激活函数：

激活函数类似于人类神经元，对输入信号进行线性或非线性变换。M-P模型中使用step函数作为激活函数，多层感知器中使用的是sigmoid函数。

除了sigmoid函数以外，激活函数还有

• tanh函数：
• 修正线性单元ReLU: 

似然函数：

多分类问题中通常采用softmax函数为似然函数。softmax函数的分母是对输出层所有单元的激活值进行求和，起到了归一化的作用，输出层中每个单元取值都是介于0和1之间的概率值（概率总和为1。），我们选择其中概率最大的类别作为最终分类结果输出。

递归问题中，有时会使用线性输出函数作为似然函数。线性输出函数会把激活值作为结果直接输出。输出层各单元的取值仍是介于0和1之间。

5、随机梯度下降法：

误差反向传播算法会先对误差函数求导计算梯度，然后计算连接权重调整值。反复迭代训练，直至获得最优解。根据训练样本的输入方式不同，误差反向传播算法又有不同的种类。

1. 批量学习算法：每次迭代计算时遍历全部训练样本。由于每次迭代都计算全部训练样本，所以能够有效抑制训练集内带噪声的样本所导致的输入模式剧烈变动；但同时由于每次调整连接权重所有样本都要参与训练，所以训练用时较长。
2. 在线学习算法：这种算法会逐个输入训练样本。由于在线学习每次迭代计算一个训练样本，所以训练样本的差异会导致迭代结果出现大幅变动。迭代结果的变动可能导致训练无法收敛。为了解决这个问题，迭代计算时可以逐渐降低学习率，但仍然存在收敛速度缓慢甚至无法收敛的情况。
3. 小批量梯度下降：将训练集分成几个子集D,每次迭代使用一个子集。全部子集迭代完成后，再次从第一个子集开始迭代调整连接权重。由于每次迭代只使用少量样本，所以和批量学习相比，小批量梯度下降法能够缩短单次训练时间。同时每次迭代使用多个训练样本，所以和在线学习相比，小批量梯度下降法能够减少迭代结果变动。小批量梯度下降法能够同时弥补在线学习和批量学习的缺点。

在线学习和小批量梯度下降法都是使用部分训练样本进行迭代计算，这种方法叫作随机梯度下降法。由于随机梯度下降法只使用部分训练样本，每次迭代后样本集的趋势都会发生变化，所以减少了迭代结果陷入局部最优解的情况。

---

学习率：用来确定权重连接调整程度的系数。

随机梯度下降法中的计算结果乘以学习率，可得到权重调整值。如果学习率过大，则有可能修正过头，导致误差无法收敛，神经网络训练效果不佳；反之，如果学习率过小，则收敛速度会很慢，导致训练时间过长。

一般按照经验确定学习率，首先设定一个较大的值，再慢慢把这个值减小；还可以自适应调整学习率，比如AdaGrad方法：用学习率除以截至当前时刻t的梯度累积值，得到神经网络的连接权重。还可以使用Adadelta方法和动量方法。Adadelta方法在求梯度累积值时只使用距离当前时刻比较近的梯度，而动量方法中，则是以指数级衰减的形式累积之前系数的梯度。

---

本人小结：深度学习是由神经网络发展而来：而神经网络的发展是由模仿单个神经元的而形成的【M-P模型】，但由于没有通过对训练样本进行训练来确定参数的方法，只能人为事先计算后确定。后来就有了能够根据训练样本确定参数的【感知器】，由于不能解决逻辑异或运算这类线性不可分问题，第一次陷入低潮。因此有了【多层感知器】，但是却没有分层训练的的办法，因此就有了【误差反向传播算法】。同一时期，也有了【神经认知机】（后一节有讲）来模拟了生物的视觉传导通路。LeCun将相当于生物初级视觉皮层的卷积层引入到神经网络中，提出了【卷积神经网络】。使用了误差反向传播算法虽然进行了分层训练，但是由于自身问题（缺少预防过拟合问题），外因（计算力有限、SVM太火），第二次陷入低潮。

如今，随着互联网的普及，获得大量的训练数据，进而抑制了过拟合问题，自身问题得到解决。同时外界环境的变化（GPU的发展和SVM的冷静），又使深度学习重新焕发新生。

 

追本溯源，这下子，历史思路清晰了，底气也足了。知史使人明智：知道了新生的原因，知道了衰败的原因。对技术的各个认知角度要有。这样才好说：系统，连贯。焕然一体，随机应变。