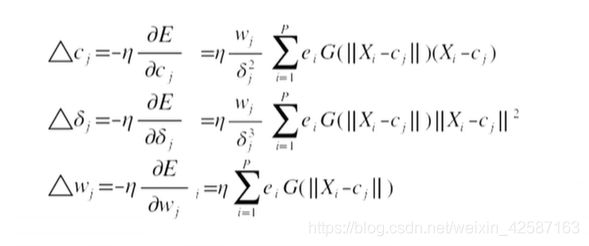神经网络(BP神经网络、RBF网络、模拟退火算法、HOPFIELD神经网络、Botzmann机)
神经网络 学习、笔记
- 神经网络发展
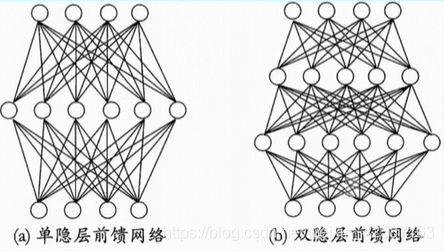
- 多层前馈神经网络
- RBF径向基函数网络
- ART自适应谐振理论网络
- SOM 自组织映射网络
- 级联相关网络
- Elman网络循环神经网络
- Botzmann机(引入较多其他概念)
-
- 爬山算法:
- 模拟退火算法
- HOPFIELD神经网络
- 玻尔兹曼分布:
- 玻尔兹曼机/随机神经网络
神经网络发展
全称人工神经网络,Artificial Neural Network, ANN
1943年,Warren McCulloch和Walter Pitts提出 M-P神经元模型;
1957年,Frank Rosenblatt 感知机Perceptron, 精确定义神经网络;
1969年,出版 感知器,提出:单层神经网络无法解决不可线性分割问题;
1986年,Hinton和David Rumelhart, 发表:Learning Representations by Back propagating errors。阐述了反向传播算法,使计算量下降到与神经元数目成正比的反向传播算法,增加一个隐层,解决了无法解决不可线性分割问题。
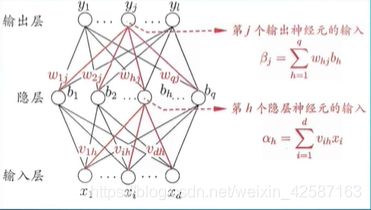
多层前馈神经网络
学习过程,就是根据训练数据来调整,神经元直之间的连接权(或称权值)和每个功能神经元的阈值(输出界值)。
误差逆传播算法(Error BackPropagation),BP算法进行训练;
输入层:只传递输入变量
功能层(隐层、输出层):既接收输入变量,同时有相应激活函数,计算后进行输出;
激活函数,可以将较大范围的数据,挤压到0-1之间,常见功能函数:

左侧阶跃函数,比较理想,1表示神经元兴奋,0表示抑制,但是不连续,不光滑等性质;一般用sigmoid.
Sigmoid函数:把可能较大范围内变化的输入值,挤压到0-1之间,也称挤压函数,有比较好求导性质:
f ′ ( x ) = e − x ( 1 + e − x ) 2 = f ( x ) ( 1 − f ( x ) ) f'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=f(x)(1-f(x)) f′(x)=(1+e−x)2e−x=f(x)(1−f(x))
可见其求导的良好性质,没有引入更多的运算。
设训练集: D = ( x ( 1 ) , y ( 1 ) ) , ( x ( 1 ) , y ( 1 ) ) , . . . , ( x ( m ) , y ( m ) ) D={(x^{(1)},y^{(1)}), (x^{(1)},y^{(1)}),..., (x^{(m)},y^{(m)})} D=(x(1),y(1)),(x(1),y(1)),...,(x(m),y(m)), 其中 x ( i ) ∈ R d , y ( i ) ∈ R l x^{(i)} \in \R^d, y^{(i)} \in \R^l x(i)∈Rd,y(i)∈Rl, 即 x x x为 d d d维 ( x 1 ( i ) , . . . x i ( i ) , . . . , x d ( i ) ) (x^{(i)}_1,...x^{(i)}_i,...,x^{(i)}_d) (x1(i),...xi(i),...,xd(i)), y y y为 l l l维 ( y 1 ( i ) , . . . y j ( i ) , . . . , y l ( i ) ) (y^{(i)}_1,...y^{(i)}_j,...,y^{(i)}_l) (y1(i),...yj(i),...,yl(i));
输入神经元: d d d个;隐层神经元: q q q个;输出神经元: l l l个;
v i h v_{ih} vih: 第 i i i个输入神经元到第 h h h个隐层神经元的权值/连接权值;
α h \alpha_h αh: 第 h h h个隐层神经元的输入值,则 α h = ∑ i = 1 d v i h x i \alpha_h=\sum_{i=1}^{d}v_{ih}x_i αh=∑i=1dvihxi;
γ h \gamma_h γh: 第 h h h个隐层神经元功能函数的阈值;
b h b_h bh: 第 h h h个隐层神经元的输出值;
b h = f ( α h − γ h ) b_h=f(\alpha_h-\gamma_h) bh=f(αh−γh)
w h j w_{hj} whj: 第 h h h个隐层神经元到第 j j j个输出神经元的权值/连接权值;
β j \beta_j βj: 第 j j j个输出神经元的输入值,则 β j = ∑ h = 1 q w h j b h \beta_j=\sum_{h=1}^{q} w_{hj}b_h βj=∑h=1qwhjbh;
θ j \theta_j θj:第 j j j个输出神经元功能函数的阈值;
y j ( k ) = f ( β j − θ j ) y^{(k)}_j=f(\beta_j-\theta_j) yj(k)=f(βj−θj)
设对某一训练数据 ( x ( k ) , y ^ ( k ) ) (x^{(k)},\hat{y}^{(k)}) (x(k),y^(k)), 设神经网络的输出为: y ( k ) = ( y 1 ( k ) , ( y 2 ( k ) , . . . ( y l ( k ) ) y^{(k)}=(y_1^{(k)}, (y_2^{(k)},...(y_l^{(k)}) y(k)=(y1(k),(y2(k),...(yl(k))
即 y j ( k ) = f ( β j − θ j ) y_j^{(k)}=f(\beta_j-\theta_j) yj(k)=f(βj−θj), 这里的阈值可以理解为 w x + b wx+b wx+b中的 − b -b −b, 也就是偏移量;
该网络在 ( x ( k ) , y ^ ( k ) ) (x^{(k)},\hat{y}^{(k)}) (x(k),y^(k))上的均方误差为: E ( k ) = 1 2 ∑ j = 1 l ( y j ( k ) − y ^ j ( k ) ) 2 E^{(k)}=\frac{1}{2}\sum_{j=1}^{l}(y_j^{(k)}-\hat{y}_j^{(k)})^2 E(k)=21∑j=1l(yj(k)−y^j(k))2
网络中参数是数量: d q + q + q l + l dq+q+ql+l dq+q+ql+l
参数更新估计式: v ← v + Δ v v \gets v+\Delta v v←v+Δv
举例(1):更新 Δ w h j = − η ∂ E ( k ) ∂ w h j \Delta w_{hj}= -\eta\frac{\partial E^{(k)}}{\partial w_{hj}} Δwhj=−η∂whj∂E(k)
∂ E ( k ) ∂ w h j = ∂ E ( k ) ∂ y j ( k ) ∂ y j ( k ) ∂ β j ∂ β j ∂ w h j = ( y j ( k ) − y ^ j ( k ) ) ⋅ y j ( k ) ( 1 − y j ( k ) ) ⋅ b h \frac{\partial E^{(k)}}{\partial w_{hj}}=\frac{\partial E^{(k)}}{\partial y_j^{(k)}}\frac{\partial y_j^{(k)}}{\partial \beta_j}\frac{\partial \beta_j}{\partial w_{hj}}=(y_j^{(k)}-\hat{y}_j^{(k)}) \cdot y_j^{(k)}(1-y_j^{(k)}) \cdot b_h ∂whj∂E(k)=∂yj(k)∂E(k)∂βj∂yj(k)∂whj∂βj=(yj(k)−y^j(k))⋅yj(k)(1−yj(k))⋅bh
令
g j = − ∂ E ( k ) ∂ y j ( k ) ∂ y j ( k ) ∂ β j = − ( y j ( k ) − y ^ j ( k ) ) ⋅ y j ( k ) ( 1 − y j ( k ) ) g_j=-\frac{\partial E^{(k)}}{\partial y_j^{(k)}}\frac{\partial y_j^{(k)}}{\partial \beta_j}=-(y_j^{(k)}-\hat{y}_j^{(k)}) \cdot y_j^{(k)}(1-y_j^{(k)}) gj=−∂yj(k)∂E(k)∂βj∂yj(k)=−(yj(k)−y^j(k))⋅yj(k)(1−yj(k))
可得:
∂ E ( k ) ∂ w h j = − g j ⋅ b h \frac{\partial E^{(k)}}{\partial w_{hj}}=-g_j\cdot b_h ∂whj∂E(k)=−gj⋅bh
Δ w h j = η g j b h \Delta w_{hj}=\eta g_j b_h Δwhj=ηgjbh
举例(2): 更新 Δ θ j = − η ∂ E ( k ) ∂ θ j = − η g i \Delta \theta_j=-\eta\frac{\partial E^{(k)}}{\partial \theta_j}=-\eta g_i Δθj=−η∂θj∂E(k)=−ηgi
∂ E ( k ) ∂ θ j = ∂ E ( k ) ∂ y j ( k ) ∂ y ( k ) ∂ θ j = ( y j ( k ) − y ^ j ( k ) ) ⋅ ( − 1 ) y j ( k ) ( 1 − y j ( k ) ) = g j \frac{\partial E^{(k)}}{\partial \theta_j}=\frac{\partial E^{(k)}}{\partial y^{(k)}_j} \frac{\partial y^{(k)}}{\partial \theta_j}=(y_j^{(k)}-\hat{y}_j^{(k)}) \cdot (-1)y_j^{(k)}(1-y_j^{(k)})=g_j ∂θj∂E(k)=∂yj(k)∂E(k)∂θj∂y(k)=(yj(k)−y^j(k))⋅(−1)yj(k)(1−yj(k))=gj
举例(3): 更新 Δ v i h = − η ∂ E ( k ) ∂ v i h = η e h x i \Delta v_{ih}=-\eta\frac{\partial E^{(k)}}{\partial v_{ih}}=\eta e_h x_i Δvih=−η∂vih∂E(k)=ηehxi
∂ E ( k ) ∂ v i h = ∑ j = 1 l ∂ E ( k ) ∂ y j ( k ) ∂ y j ( k ) ∂ β j ∂ β j ∂ b h ∂ b h ∂ α h ∂ α h ∂ v i h = ∑ j = 1 l ( − g j ) ⋅ ∂ β j ∂ b h ∂ b h ∂ α h ∂ α h ∂ v i h = ∑ j = 1 l ( − g j ) ⋅ w h j ⋅ b h ( 1 − b h ) ⋅ x i \begin{aligned} \frac{\partial E^{(k)}}{\partial v_{ih}} &=\sum_{j=1}^{l}\frac{\partial E^{(k)}}{\partial y^{(k)}_j} \frac{\partial y^{(k)}_j}{\partial \beta_j} \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \alpha_h}\frac{\partial \alpha_h}{\partial v_{ih}}\\ &=\sum_{j=1}^{l}(-g_j)\cdot \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \alpha_h}\frac{\partial \alpha_h}{\partial v_{ih}}\\ &=\sum_{j=1}^{l}(-g_j)\cdot w_{hj} \cdot b_h(1-b_h)\cdot x_i \end{aligned} ∂vih∂E(k)=j=1∑l∂yj(k)∂E(k)∂βj∂yj(k)∂bh∂βj∂αh∂bh∂vih∂αh=j=1∑l(−gj)⋅∂bh∂βj∂αh∂bh∂vih∂αh=j=1∑l(−gj)⋅whj⋅bh(1−bh)⋅xi
令:
e h = − ∂ E ( k ) ∂ b h ∂ b h ∂ α h = b h ( 1 − b h ) ∑ j = 1 l w h j g j e_h=-\frac{\partial E^{(k)}}{\partial b_h}\frac{\partial b_h}{\partial \alpha_h}=b_h(1-b_h)\sum_{j=1}^{l}w_{hj}g_j eh=−∂bh∂E(k)∂αh∂bh=bh(1−bh)j=1∑lwhjgj
则:
∂ E ( k ) ∂ v i h = ( − e h ) ⋅ x i \frac{\partial E^{(k)}}{\partial v_{ih}}=(-e_h)\cdot x_i ∂vih∂E(k)=(−eh)⋅xi
Δ v i h = − η ⋅ ( − e h ) ⋅ x i = η e h x i \Delta v_{ih}=-\eta \cdot (-e_h) \cdot x_i=\eta e_h x_i Δvih=−η⋅(−eh)⋅xi=ηehxi
举例(4):更新 Δ γ h = − η ∂ E ( k ) ∂ γ h = − η e h \Delta \gamma_h=-\eta \frac{\partial E^{(k)}}{\partial \gamma_h}=-\eta e_h Δγh=−η∂γh∂E(k)=−ηeh
∂ E ( k ) ∂ γ h = ∑ j = 1 l ∂ E ( k ) ∂ y j ( k ) ∂ y j ( k ) ∂ β j ∂ β j ∂ b h ∂ b h ∂ γ h = ∑ j = 1 l ( − g j ) ⋅ ∂ β j ∂ b h ∂ b h ∂ γ h = ∑ j = 1 l ( − g j ) ⋅ w h j ⋅ − b h ( 1 − b h ) = e h \begin{aligned} \frac{\partial E^{(k)}}{\partial \gamma_h} &=\sum_{j=1}^{l}\frac{\partial E^{(k)}}{\partial y^{(k)}_j} \frac{\partial y^{(k)}_j}{\partial \beta_j} \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \gamma_h}\\ &=\sum_{j=1}^{l}(-g_j)\cdot \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \gamma_h}\\ &=\sum_{j=1}^{l}(-g_j)\cdot w_{hj} \cdot -b_h(1-b_h)\\ &=e_h \end{aligned} ∂γh∂E(k)=j=1∑l∂yj(k)∂E(k)∂βj∂yj(k)∂bh∂βj∂γh∂bh=j=1∑l(−gj)⋅∂bh∂βj∂γh∂bh=j=1∑l(−gj)⋅whj⋅−bh(1−bh)=eh
所以 Δ γ h = − η e h \Delta \gamma_h=-\eta e_h Δγh=−ηeh
接下来总结BP算法的流程:
输入: 训练集 D = { ( x ( k ) , y ^ ( k ) ) } k = 1 m D=\{(x^{(k)}, \hat{y}^{(k)})\}_{k=1}^m D={ (x(k),y^(k))}k=1m, 学习率 η \eta η
过程:
- 在(0,1)范围内随机初始化网络中所有连接权和阈值;
- repeat
- for all ( x ( k ) , y ^ ( k ) ) ∈ D (x^{(k)}, \hat{y}^{(k)})\in D (x(k),y^(k))∈D do:
(1)计算当前参数,计算当前样本的输出 y ( k ) {y}^{(k)} y(k);
(2)计算输出层神经元的梯度项 g j g_j gj;
(3)计算隐层神经元的梯度项 e h e_h eh;
(4)根据上文计算公式,更新连接权 w h j , v i h w_{hj}, v_{ih} whj,vih和阈值 θ j , γ h \theta_j, \gamma_h θj,γh;
(5) end for - until 达到停止条件(如训练误差)
输出:连接权与阈值确定的多层前馈神经网络
以上是标准误差逆传播算法(error Backpropagation)。
还有一种方法是累计误差逆传播算法(accumulated errorbackpropagation), 不再用某个数据的误差进行迭代,而是用所有数据误差的均值:
E = 1 m ∑ k = 1 m E k E=\frac{1}{m} \sum_{k=1}^{m} E_k E=m1k=1∑mEk
标准误差逆传播算法:更新针对单个样例,参数更新非常频繁;对不同样例更新,可能出现相互抵消现象;因此,可能需要更多次数的迭代。
累计误差逆传播算法:直接针对累计误差最小化,遍历完整个数据集后,才更新一次参数,参数更新频率低很多;但很容易到极值点,进一步下降就会非常缓慢,所以收敛速度往往不如标准BP快;尤其在大数据集时,标准BP优势明显。
RBF径向基函数网络
RBF(Radial Basis Function, 径向基函数)网络。
径向基函数:取值仅依赖于离原点(或到中心点c)距离的实质函数
ϕ ( x ) = ϕ ( ∣ ∣ x ∣ ∣ ) \phi (x)=\phi(\mid\mid x\mid\mid) ϕ(x)=ϕ(∣∣x∣∣)
ϕ ( x , c ) = ϕ ( ∣ ∣ x − c ∣ ∣ ) \phi (x, c)=\phi(\mid\mid x-c\mid\mid) ϕ(x,c)=ϕ(∣∣x−c∣∣)
如,可取高斯径向基函数:
h ( x ) = e x p ( − ( x − c ) 2 r 2 ) h(x)=exp\big( - \frac{(x-c)^2}{r^2}\big) h(x)=exp(−r2(x−c)2)
径向基函数一般作为隐层神经元的激活函数,而输出层则是对隐层神经元输出的线性组合。
它能以任意精度逼近任意连续函数,特别适合用于解决分类问题。(证明?)
RBF结构:

第一层输入层为信号源结点;
第二层为隐层,单元数目根据需要设定,隐单元激活函数为RBF径向基函数,对中心点径向对称的衰减非负非线性函数;
第三层输出层,对输入模式做出响应;
径向基函数构成隐层空间,可以将输入矢量映射到该空间(一般为高维,看选择单元数),低维不可分数据映射到该高维空间,可能就变的可分。
隐层功能:将低维空间的输入通过非线性函数转换成高维空间,可在高维空间内去寻找最合适的拟合训练。
隐层到输出层是线性的加权和,加大学习速度,避免局部极小值。
RBF网络参数:径向基函数中心点 c j c_j cj,方差 σ \sigma σ和隐层到输出层的权值 w j w_{j} wj
y ( k ) = ∑ j = 1 h w j e x p ( − 1 2 ( σ ) 2 ∣ ∣ x ( k ) − c j ∣ ∣ 2 ) y^{(k)}=\sum_{j=1}^{h} w_{j}exp(-\frac{1}{2(\sigma)^2} \mid\mid x^{(k)}-c_j\mid\mid^2) y(k)=j=1∑hwjexp(−2(σ)21∣∣x(k)−cj∣∣2)
学习方法1:
(1)非监督方法得到径向基函数的中心和方差;
(2)监督方法(最小均方误差)得到隐含层到输出层权值。(详细计算方法后续有时间补充。。。)

其中,通过聚类是指通过KNN等方法进行聚类,将聚类中心当做h个中心, c m a x c_{max} cmax为所选取中心间最大距离,可避免径向基函数太尖锐或太平。
学习方法2:监督学习方法对所有参数进行训练。主要是对代价函数(均方误差)进行梯度下降:
(1) 随机初始化径向基函数的中心,方差和隐含层到输出层的权值。当然,也可用1方法来初始化;
(2)通过梯度下降法对网络中三种参数进行监督训练优化。代价函数是网络输出和期望输出的均方误差:
E = 1 2 ( y ( x ) − d ) 2 E=\frac{1}{2}(y(x)-d)^2 E=21(y(x)−d)2
每次迭代,在误差梯度的负方向以一定的学习率调整参数。
ART自适应谐振理论网络
Adaptive Resonance Theory。
1976年, Carpenter 提出自适应共振理论;
1978年,G.A.Carpenter 与S. Grossberg 提出ATR网络。
ART网络是竞争型学习competitive learning 的代表,有三种形式:
ART I型处理双极型或二进制信号
ART II型处理连续型模拟信号
ART III型分级搜索模型
竞争型含义:一种常用无监督学习策略,使用时,网络的输出神经元相互竞争,同一时刻有且仅有一个获胜的神经元被激活,其他被抑制,也称胜者通吃winner take all 原则。
对于有监督学习网络,通过反复输入样本模式进行学习,加入新样本训练时,前面的训练结果可能会受影响,表现为对旧知识的遗忘。
而无监督学习的权值调整,学习包含了对数据的学习项和对旧数据忘却项,通过控制学习系数和忘却系数大小达到某种折中,但系数确定无确定方法,所以也可能会出现忘却旧样本情况。
通过无线扩大网络规模解决样本遗忘, 不现实。而ART网络,是在适当增加网络规模同时,在过去和新模式中做出折中,最大限度接受新知识,同时较少影响过去模式或样本,灵活性和稳定性相统一。

基本思路:
(1)按照预设定的参考门限检查输入模式与之前存储的所有模式类典型向量之间的匹配程度,以确定相似度;
(2)对相似度超过门限的所有模式类,选择最相似的作为该模式的代表类,并调整与该类别相关的权值;使后续与该模式相似的输入,与该模式匹配时得到更大的相似度;
(3)若相似度未超过门限,网络中新建模式类,同时建立与其相连的权值,存储该模式和后来输入所有同类模式。
ART网络:比较层、识别层,识别阈值和重置模块构成。
比较层:负责接收输入样本,将其传递给识别层神经元;
识别层:每个神经元对应一个模式类,神经元数目可在训练过程中动增长以增加新模式类。
ART I网络结构:
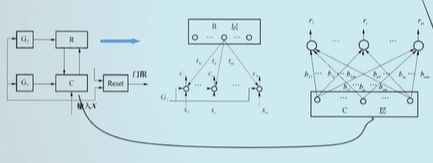
两层神经网络,比较层C,识别层R。
三种控制信号: 复位信号,逻辑控制信号G1和G2。
接收到输入层信号时,识别层神经元相互竞争,计算输入向量与每个识别层神经元模式向量之间距离,距离小的获胜;获胜神经元加上其他的识别层神经元,发送信号,抑制激活。如果相似度不大于阈值,则重置模块在识别层增设新神经元,代表向量为当前输入向量。
具有良好学习新知识能力和稳定性。可有效进行增量学习或在线学习。
SOM 自组织映射网络
Self Organizing Map, Kohonen 1982.
竞争学习型无监督神经网络。
高维降维方法,通常降为2维,同时保证高维空间的拓扑结构,也就是将高维相似的映射到网络输出层当中邻近的神经元。
可用于可视化,聚类等。

竞争学习规则-Winner-Take-All
主要用于分类(分类)和聚类(无监督)
各神经元对应的权重向量全部进行归一化,使 W W W的模全为1,归一化后,相似度最大就是内积最大;依次判断竞争获胜神经元,其实就是在单位圆中寻找夹角最小点,得到获胜神经元后,调整神经元。
W ^ j ∗ T X ^ = m a x j ∈ { 1 , 2 , . . . , m } ( W ^ j T X ^ ) \hat{W}_{j*}^T\hat{X}=max_{j \in \{1,2,...,m\}} (\hat{W}_j^T\hat{X}) W^j∗TX^=maxj∈{ 1,2,...,m}(W^jTX^)
调整权重:
o j ( t + 1 ) = { 1 , j = j ∗ 0 , j ≠ j ∗ o_j(t+1)=\begin{cases} 1 , j=j^*\\ 0 , j\ne j^*\end{cases} oj(t+1)={ 1,j=j∗0,j=j∗
W j ∗ ( t + 1 ) = W ^ j ∗ ( t ) + Δ W j ∗ = W ^ j ∗ ( t ) + η ( t ) ( X ^ − W ^ j ∗ ) W_{j*}(t+1)=\hat{W}_{j*}(t)+\Delta W_{j*}=\hat{W}_{j*}(t)+\eta(t)(\hat{X}-\hat{W}_{j*}) Wj∗(t+1)=W^j∗(t)+ΔWj∗=W^j∗(t)+η(t)(X^−W^j∗)
W j ( t + 1 ) = W ^ j ( t ) , j ≠ j ∗ W_j(t+1)=\hat{W}_j(t), j\ne j^* Wj(t+1)=W^j(t),j=j∗
SOM网络训练过程:
接收到一个训练样本后,每个输出层神经元会计算该样本与自身携带的权向量之间距离,距离最近神经元成为竞争获胜者,称为最佳匹配单元best matching unit;
然后,最佳匹配单元及其邻近神经元的权向量将被调整,以使得这些权向量与当前输入样本距离缩小;
过程不断迭代,直至收敛。
级联相关网络
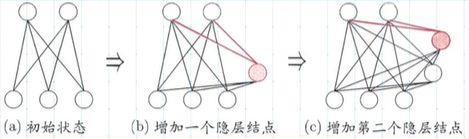
Cascade-Correlation, 1990 Fahlman and Lcbiere, 是结构自适应网络的重要代表,把网络结构当做学习的目标之一;
两个主要成分:‘级联’和‘相关’
级联:建立层次连接的层级结构,开始时,只有输入层,输出层,处于最小拓扑结构,训练进行,逐渐加入隐层神经元,新加入后其输入端连接权值冻结固定;
相关:最大化新神经元的输出与网络误差之间的相关性来训练相关参数。
无需设置网络层数,隐层神经元数目,且训练速度较快,但其在数据较小时易陷入过拟合。
Elman网络循环神经网络
Elman 1990提出,属于Recurrent neural networks, 循环神经网络。
允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号,能处理与时间有关的动态变化,语音处理时经常使用。
隐层神经元的输出被反馈回来,与下一时刻的输入信号一起输入隐层神经元,通常采用sigmoid激活函数。网络训练常采用推广的BP算法进行。
LSTM 长短时存储网络,就是由该网络发展而来。
Botzmann机(引入较多其他概念)
全称 玻尔兹曼学习机。
Hinten和Ackley发明,1985年,一种随机的递归神经网络。能通过学习数据的固有内在表示来解决困难问题,因样本分布遵循玻尔兹曼分布而命名。
在此需引入一堆新概念/算法,如果要比较好的应用,建议需要耐心慢慢看完,慢慢理解:
首先引入简单的爬山算法
爬山算法:
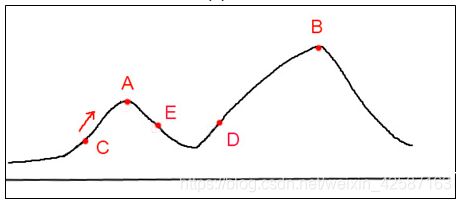
爬山算法是一种贪心算法,该算法每次从当前解空间选取一个解作为最优解,直到达到一个局部最优解,设函数 f ( x ) f(x) f(x)图像如下,用爬山算法求其最大值,若C为当前最优解,则爬山算法搜索到A就会停止搜索,从而获得一个局部最优解,但不是全部最优解;
模拟退火算法
引入模拟退火算法,Simulated Annealing, SA
参考 这里讲的比较易懂
爬山算法搜索到A就会停止,因为A左右的值均小于A的值。而模拟退火算法采用的解决办法是以一定的概率选择A两边的点,尽管A两边的点不是局部最优解,甚至不如A点更优,这样就有一定概率搜索到D点,从而有一定概率搜索到B点,最终获得全局最优解。至于是以怎样的概率跳出了局部最优点,是模拟退火算法的精髓,为了解决局部最优问题,1983年,Kirkpatrik等提出模拟退火算法SA,能有效解决该问题。如下进行介绍:
首先大家了解下退火的大概原理:在分子原子世界中,能量越大,意味着分子和原子越不稳定,当能量越低时,原子越稳定。‘退火’是物理术语,指对物体加温再冷却的过程,既然要冷却为何要加温呢?
因为晶体冷却过程中,如果固体不处于最低能量状态,需要给固体加热再冷却,随着温度缓慢下降,固体中的原子按照一定形状排列,形成高密度,低能量的有规则晶体,对应于算法中的全局最优解;
如果冷却温度下降过快,可能导致原子缺少足够时间排列成晶体结构,结果会产生具有较高能量的非晶体,也就是我们所说的局部最优解。
因此可以根据退火过程,给其增加一点能量,然后再冷却,如果增加能量跳出了局部最优解,则本次退火就是成功的。
模拟退火算法包含两个部分,Metropolis算法和退火过程。Metropolis算法是退火的基础,解释了如何在局部最优解情况下让其跳出来。1953年Metropolis提出该采样方法,即以概率来接受新状态,而不是使用完全确定的规则,称为Metropolis准则,计算量较低。下面进行说明:
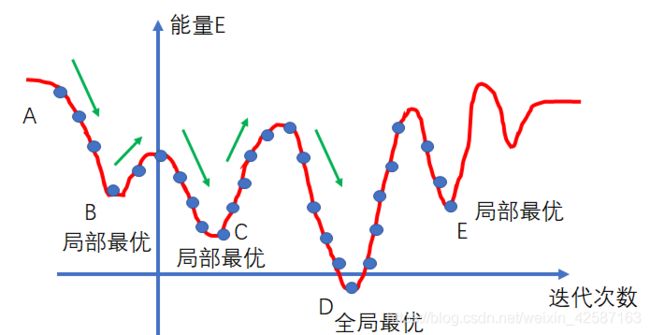
如上图,我们可把能量当做优化算法的代价函数/损失函数 f ( x ) f(x) f(x) (当成能量E,即是物理意义上的退火;当成 f ( x ) f(x) f(x), 即为算法中优化损失函数过程),退火模拟算法优化损失函数,假设开始状态A,随着迭代次数更新到B的局部最优解,此时发现更新到B时, E E E / f ( x ) f(x) f(x)比A要低,说明接近最优解,因此百分百转移;状态到B后,发现下一步 E E E / f ( x ) f(x) f(x)上升了,如果是梯度下降法/爬山算法,是不允许继续前进,而这里则会以一定概率跳出这里,而这个概率和当前状态、能量等都有关系。
上面过程从数学角度考虑:
假设前一个状态为 x ( n ) x(n) x(n), 系统根据某一指标(如梯度下降),状态变为 x ( n + 1 ) x(n+1) x(n+1), 相应地,系统能量从 E ( n ) E(n) E(n)变为 E ( n + 1 ) E(n+1) E(n+1), 定义系统从 x ( n ) x(n) x(n)变为 x ( n + 1 ) x(n+1) x(n+1)的接受概率为:
P = { 1 , 当 E ( n + 1 ) < E ( n ) 时 1 , 当 E ( n + 1 ) ≥ E ( n ) , 且 P ∗ = e − E ( n + 1 ) − E ( n ) T > ε 时 0 , 当 E ( n + 1 ) ≥ E ( n ) , 且 P ∗ = e − E ( n + 1 ) − E ( n ) T ≤ ε 时 P=\begin{cases} 1 , 当E(n+1)
ε \varepsilon ε: 为在区间 [ 0 , 1 ] [0,1] [0,1]中产生的一个均匀分布的随机数
上式看到,如果能量减小了,那么这种转移就会被接受( P = 1 P=1 P=1),如果能量增大了,说明可能系统偏离全局最优更远了,但是它不会像爬山算法一样,马上摒弃,而是进行概率操作:首先在区间 [ 0 , 1 ] [0,1] [0,1]中产生一个均匀分布的随机数 ε \varepsilon ε ,计算 P ∗ P^* P∗, 如果 ε < P ∗ \varepsilon
P ∗ = e − E ( n + 1 ) − E ( n ) T P^*=e^{-\frac{E(n+1)-E(n)}{T}} P∗=e−TE(n+1)−E(n)
退火算法参数控制: T T T比较高时, P ∗ P^* P∗较大,显然此时未达到最佳冷却状态,倾向于进行退火,而随着冷却进行, T T T的减小, P ∗ P^* P∗会减小,比 ε \varepsilon ε大的概率会越来越小,越倾向于不进行加温再冷却。
对应到算法里,并不存在温度这样一个物理变量,但是 T T T可等价于一个关于时间 t t t(或理解为总迭代次数)的函数,先令 T = t T=t T=t开始迭代时, t t t较小遇到局部最优时,倾向于跳出,而随着 t t t增大,大概率离全局最优更近, P ∗ P^* P∗减小,转移的概率相应会减小。
但是直接使用Metropolis算法, T = t T=t T=t,可能导致寻优速度太慢,以至于实际无法使用,为了确保有限时间内收敛,必须设定控制算法收敛的参数,上面公式中,如果 T T T过大,也就是转移概率会比较大,经过更频繁的转移,可能会导致退火太快,达到局部最优就会结束迭代,如果 T T T太小,则计算时间会增加,实际中采用退火温度表,退火初期采用大 T T T值,随着退火进行,逐步降低,具体有以下几个方面考量:
(1)较高的初始温度/参数T(0):使开始时所有转移都尽量被接受,初始越高,获得高质量解概率越大,但耗费时间会越长;
(2)退火速率:简单的方法是采用指数下降方式:
T ( n + 1 ) = λ T ( n ) , n = 1 , 2 , 3 , . . . T(n+1)=\lambda T(n), n=1,2,3,... T(n+1)=λT(n),n=1,2,3,...
其中 λ \lambda λ是小于1的整数,一般取为 0.8 − 0.99 0.8-0.99 0.8−0.99之间,使其对每一温度,都有足够的转移尝试,但指数式下降收敛速度比较慢,其他下降方式如下:
T ( n ) = T ( 0 ) log ( 1 + t ) T(n)=\frac{T(0)}{\log(1+t)} T(n)=log(1+t)T(0)
T ( n ) = T ( 0 ) 1 + t T(n)=\frac{T(0)}{1+t} T(n)=1+tT(0)
(3)终止温度:如果在若干次迭代后,没有可以更新的新状态,或没有达到用户设定的阈值,则退火完成。
综上后,退火算法程序流程可总结如下:
(1) 初始化:初始“温度” T T T(充分大,之所以“温度”带引号,意思是并非真正的物理温度,而是可当做算法里的一个关于时间的参数),随机生成初始状态或随机生成初始参数为 w w w(是算法迭代起点),损失函数为 f ( w ) f(w) f(w),每 T T T值最大迭代 L L L次;
(2)对 k = 1 , 2 , . . . , L k=1,2,...,L k=1,2,...,L做第(3)至第(6)步;
(3)扰动产生新 w ′ w' w′,计算新损失函数值 f ( w ′ ) f(w') f(w′);
(4)计算损失函数增量 Δ f = f ( w ′ ) − f ( w ) \Delta f=f(w')-f(w) Δf=f(w′)−f(w);
(5)若 Δ f < 0 \Delta f<0 Δf<0(图中为 ≤ 0 \le 0 ≤0), 则接受新解,否则用Metropolis准则判断是否接受 w ′ w' w′;
(6)判断当前迭代 k k k是否到达该 T T T设置迭代次数 L L L, 若没超过,返回第(3)步,若迭代次数达到 L L L, 则进入(7);
(7)判断是否满足终止条件,若不满足,更新温度为 T ′ T' T′, 在新 T ′ T' T′下返回到第(2)步;
(8)如上循环,直至满足终止条件,运算结束,输出结果。

事实上,模拟退火算法与初始值无关,算法求得的解与初始状态 w w w无关, 且具有渐近收敛性,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法,且具有并行性。
HOPFIELD神经网络
引入HOPFIELD神经网络:
比较好的参考:这里,但原文符号有点乱,下面进行了统一化
上文探讨了BP前馈式神经网络,但同时另一个神经网络也很重要,为Hopfield神经网络,是反馈式。其学习规则是基于灌输式学习,网络的权值不是通过训练出来的,而是按照一定规则计算出来的,Hopfield神经网络便是此学习方式,其权值一旦确定便不再更改,而网络中各神经元状态在运行过程不断更新,网络演变到稳定时,各神经元的状态便是问题解。
Hopfield神经网络分为离散型和连续型两种网络模模型,分别记为DHNN(Discrete Hopfield Neural Network)和CHNN (Continues Hopfield Neural Network), 这里主要探讨离散型。
Hopfield最早提出的网络便是二值神经网络,各神经元激励函数为阶跃或双极值函数,神经元的输入输出只取{0, 1}或{-1, 1}。1和0或1和-1分别表示神经元处于激活状态和抑制状态。
离散Hopfield DHNN是一个单层网络,有n个神经元结点,每个输出均接到其他神经元的输入。各结点没有自反馈,每个结点都可处于一种可能的状态(如1或-1),即当该神经元所受刺激超过阈值时,处于一种激活状态(如1), 否则始终处于另一状态(如-1)。
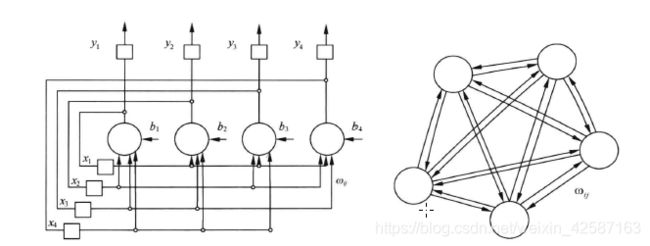
右图相当于忽略了输出输入分枝后,得到的简化图,更容易看出其神经元互联特点, 此时Hopfield网络成了单层全互连网络。
Hopfield网络的稳定性:Hopfield网络按照神经动力学方式运行,对于给定初始状态按照能量减少方式演化,最终达到稳定状态。
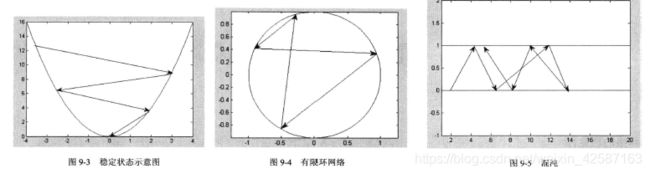
(1)DHNN网络实质为一个离散的非线性动力学系统,网络从初态 x ( 0 ) x(0) x(0)开始,若能经有限次递归后,其状态不再发生变化,即 x ( t + 1 ) = x ( t ) x(t+1)=x(t) x(t+1)=x(t),则称该网络是稳定的;
(2)如果网络是稳定的,它可以从任一初态收敛到一个稳态;
(3)若网络是不稳定的,由于DHNN网每个节点只有1和-1两种情况,网络不可能出现无限发散情况,只能出现限幅的自持振荡,这种网络称为有限环网络;
(4)在有限环网络中,系统在确定的几个状态之间循环往复,系统也可能不稳定收敛于一个确定状态,而是在无限多个状态之间变化,但是轨迹不发散到无穷远,这种现象叫混沌;
对于中间层(神经元层),任意两个神经元链接权值为 w i j w_{ij} wij (定义为神经元 i i i的输出,连接到神经元 j j j的输入的连接权), 一般定义神经元连接有对称性,即 w i j = w j i w_{ij}=w_{ji} wij=wji。上面提到各神经元应无自反馈,即 w i i = 0 w_{ii}=0 wii=0, 如此保证神经元自身无连接,称为无自反馈Hopfield网络,如果 w i i w_{ii} wii 不为0, 则对应有自反馈的Hopfield网络,但出于稳定性考虑,应避免具有自反馈的网络。
除了权值参数 w w w外,每个神经元还有一个自己的阈值 b i b_i bi(有些地方会记作 T i T_i Ti,且定义往往相反,即 T i = − b i T_i=-b_i Ti=−bi, 但不影响使用,为避免大家混乱,此处统一记作 b i b_i bi, 可理解为线性模型中" w x + b wx+b wx+b"中的阈值b), 每个神经元的输出 y i y_i yi会被再次作为 x i x_i xi(统一符号,后续输出状态也用 x i 来 表 示 x_i来表示 xi来表示),作为各个神经元的输入的一部分,返回到各神经元。
数学角度来分析DHNN网络:
DHNN的输入就是网络的状态初始值,表示为 X ( 0 ) = [ x 1 ( 0 ) , x 2 ( 0 ) , . . . , x n ( 0 ) ] T X(0)=[x_1(0), x_2(0),...,x_n(0)]^T X(0)=[x1(0),x2(0),...,xn(0)]T;
DHNN在外界输入激发下,从初始状态进入动态演变过程,变化规律为 x j ( t + 1 ) = f ( n e t j ( t ) ) x_j(t+1)=f(net_j(t)) xj(t+1)=f(netj(t)), n e t j ( t ) net_j(t) netj(t)表示 t t t时 j j j神经元该时的净输入, f f f为其转移函数。转移符号常用如下:
x j ( t + 1 ) = s g n ( n e t j ( t ) ) = { 1 , 当 n e t j ( t ) ≥ 0 时 − 1 , 当 n e t j ( t ) < 0 时 x_j(t+1)=sgn(net_j(t))=\begin{cases} 1, 当net_j (t)\ge 0时\\ -1, 当net_j (t)< 0时\\ \end{cases} xj(t+1)=sgn(netj(t))={ 1,当netj(t)≥0时−1,当netj(t)<0时
n e t j ( t ) = ∑ i = 1 n ( w i j x i ( t ) ) + b j net_j(t)=\sum_{i=1}^n(w_{ij}x_i(t))+b_j netj(t)=i=1∑n(wijxi(t))+bj
对于DHNN网络,一般有 w i i = 0 , w i j = w j i w_{ii}=0, w_{ij}=w_{ji} wii=0,wij=wji。
当网络每个神经元状态不再改变时,此时状态就是网络的最后输出稳态,表示为: lim t → ∞ x ( t ) \lim_{t\rightarrow\infty} x(t) limt→∞x(t)
引入吸引子,吸引域:
吸引子:网络达到稳定时的状态 X ^ = ( x ^ 1 , x ^ 2 , . . . , x ^ n ) \hat{X}=(\hat{x}_1,\hat{x}_2,..., \hat{x}_n) X^=(x^1,x^2,...,x^n),称为网络吸引子;
吸引域:能够最终演化为吸引子的初始状态 X ( 0 ) X(0) X(0)的集合为该吸引子的吸引域;
具体地:若网络状态 X X X满足 X = f ( W X + B ) X=f(WX+B) X=f(WX+B), 则称X为网络的吸引子。
引入异步(串行)更新方式和同步(并行)更新方式:
(1)异步(串行):网络运行时每次只有一个神经元 i i i进行转态更新,其他神经元状态权值不变,即:
x j ( t + 1 ) = { s g n ( n e t j ( t ) ) , 当 j = i 时 x j ( t ) , 当 j ≠ i 时 x_j(t+1)=\begin{cases} sgn(net_j(t)), 当j=i时\\ x_j(t), 当j \ne i时\\ \end{cases} xj(t+1)={ sgn(netj(t)),当j=i时xj(t),当j=i时
神经元状态更新顺序可以按照预先设定的顺序进行调整,也可以随机选定。
(2)同步(并行):和异步相比,网络同步工作方式为一种并行方式,所有神经元同时调整状态,即:
x j ( t + 1 ) = s g n ( n e t j ( t ) ) , j = 1 , 2 , 3 , . . . , n x_j(t+1)=sgn(net_j(t)), j=1,2,3,...,n xj(t+1)=sgn(netj(t)),j=1,2,3,...,n
网络计算的过程就是初始输入向量经过逐次迭代向吸引子演化的过程,演化规则是向能量函数减小的方向演化,直到最终达到稳定状态。能量函数的定义(定义出处一直没找到):
E = − 1 2 X T W X − X T B = − 1 2 ( x 1 , x 2 , . . . , x n ) ( w 11 w 12 . . . w 1 n w 21 w 22 . . . w 2 n . . . . . . . . . . . . w n 1 w n 2 . . . w n n ) ( x 1 x 2 . . . x n ) − ( x 1 , x 2 , . . . x n ) ( b 1 b 2 . . . b n ) = − 1 2 ( x 1 , x 2 , . . . , x n ) ( ∑ j = 1 n w 1 j x j ∑ j = 1 n w 2 j x j . . . ∑ j = 1 n w n j x j ) − ∑ i = 1 n b i x i = − 1 2 ∑ i = 1 n ∑ j = 1 n w i j x j x i − ∑ i = 1 n b i x i \begin{aligned} E &=-\frac{1}{2}X^TWX-X^TB\\ &=-\frac{1}{2}(x_1,x_2,...,x_n)\begin{pmatrix} w_{11} & w_{12}& ...&w_{1n}\\ w_{21} &w_{22} & ...&w_{2n} \\...&...&...&...\\ w_{n1} &w_{n2}&...&w_{nn}\end{pmatrix} \begin{pmatrix} x_1 \\x_2\\ ...\\x_n\end{pmatrix}-(x_1,x_2,...x_n)\begin{pmatrix} b_1\\ b_2 \\... \\ b_n\end{pmatrix}\\ &=-\frac{1}{2}(x_1,x_2,...,x_n)\begin{pmatrix} \sum_{j=1}^n w_{1j}x_j\\ \sum_{j=1}^n w_{2j}x_j \\...\\ \sum_{j=1}^n w_{nj}x_j\end{pmatrix}-\sum_{i=1}^nb_ix_i\\ &=-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^nw_{ij}x_jx_i-\sum_{i=1}^nb_ix_i \end{aligned} E=−21XTWX−XTB=−21(x1,x2,...,xn)⎝⎜⎜⎛w11w21...wn1w12w22...wn2............w1nw2n...wnn⎠⎟⎟⎞⎝⎜⎜⎛x1x2...xn⎠⎟⎟⎞−(x1,x2,...xn)⎝⎜⎜⎛b1b2...bn⎠⎟⎟⎞=−21(x1,x2,...,xn)⎝⎜⎜⎛∑j=1nw1jxj∑j=1nw2jxj...∑j=1nwnjxj⎠⎟⎟⎞−i=1∑nbixi=−21i=1∑nj=1∑nwijxjxi−i=1∑nbixi
以上给出了矩阵及数值计算公式。
对于DHNN网络,已被证明:
若按异步串行方式调整网络状态,且连接权矩阵 W W W为对称阵,则对于任意初态,网络都最终收敛到一个吸引子;
若按同步并行方式调整网络状态,且连接权为非负定对称矩阵,则对于任意状态,网络最终都收敛于一个吸引子。
- 异步收敛证明:
对异步串行收敛到一个吸引子的证明:
令网络的能量改变量为 Δ E \Delta E ΔE, 状态改变量为 Δ X \Delta X ΔX, 显然有:
Δ E ( t ) = E ( t + 1 ) − E ( t ) \Delta E(t)=E(t+1)-E(t) ΔE(t)=E(t+1)−E(t)
Δ X ( t ) = X ( t + 1 ) − X ( t ) \Delta X(t)=X(t+1)-X(t) ΔX(t)=X(t+1)−X(t)
由以上两式及能量公式,得:
Δ E ( t ) = − 1 2 X T ( t + 1 ) W X ( t + 1 ) − X T ( t + 1 ) B + 1 2 X T ( t ) W X ( t ) + X T ( t ) B = − 1 2 ( X ( t ) + Δ X ( t ) ) T W ( X ( t ) + Δ X ( t ) ) − ( X ( t ) + Δ X ( t ) ) T B + 1 2 X T ( t ) W X ( t ) + X T ( t ) B = ( − 1 2 X T ( t ) W X ( t ) − 1 2 X T ( t ) W Δ X ( t ) − 1 2 Δ X T ( t ) W X ( t ) − 1 2 Δ X T ( t ) W Δ X ( t ) + 1 2 X T ( t ) W X ( t ) ) + ( X T ( t ) B − ( X ( t ) + Δ X ( t ) ) T B ) = − Δ X T ( t ) W X ( t ) − 1 2 Δ X T ( t ) W Δ X ( t ) − Δ X T ( t ) B = − Δ X T ( t ) [ W X ( t ) + B ] − 1 2 Δ X T ( t ) W Δ X ( t ) \begin{aligned}\Delta E(t) &=-\frac{1}{2}X^T(t+1)WX(t+1)-X^T(t+1)B+\frac{1}{2}X^T(t)WX(t)+X^T(t)B\\ &=-\frac{1}{2}(X(t)+\Delta X(t))^TW(X(t)+\Delta X(t))-(X(t)+\Delta X(t))^TB+\frac{1}{2}X^T(t)WX(t)+X^T(t)B\\ &=\big(-\frac{1}{2}X^T(t)WX(t)-\frac{1}{2}X^T(t)W\Delta X(t) -\frac{1}{2}\Delta X^T(t)WX(t) -\frac{1}{2}\Delta X^T(t)W\Delta X(t)+\frac{1}{2}X^T(t)WX(t)\big)+\big(X^T(t)B-(X(t)+\Delta X(t))^TB\big)\\ &=-\Delta X^T(t)WX(t)-\frac{1}{2} \Delta X^T(t)W\Delta X(t)-\Delta X^T(t)B\\ &=-\Delta X^T(t)[WX(t)+B]-\frac{1}{2} \Delta X^T(t)W\Delta X(t) \end{aligned} ΔE(t)=−21XT(t+1)WX(t+1)−XT(t+1)B+21XT(t)WX(t)+XT(t)B=−21(X(t)+ΔX(t))TW(X(t)+ΔX(t))−(X(t)+ΔX(t))TB+21XT(t)WX(t)+XT(t)B=(−21XT(t)WX(t)−21XT(t)WΔX(t)−21ΔXT(t)WX(t)−21ΔXT(t)WΔX(t)+21XT(t)WX(t))+(XT(t)B−(X(t)+ΔX(t))TB)=−ΔXT(t)WX(t)−21ΔXT(t)WΔX(t)−ΔXT(t)B=−ΔXT(t)[WX(t)+B]−21ΔXT(t)WΔX(t)
因为是异步串行更新方式,所以状态改变量为:
Δ X ( t ) = ( 0 , 0 , . . . , Δ x j ( t ) , . . . , 0 ) T \Delta X(t)=(0,0,...,\Delta x_j(t),...,0)^T ΔX(t)=(0,0,...,Δxj(t),...,0)T
带入上式:
Δ E ( t ) = − ( 0 , 0 , . . . Δ x j ( t ) , . . . , 0 ) ( ( w 11 w 12 . . . w 1 n w 21 w 22 . . . w 2 n . . . . . . . . . . . . w n 1 w n 2 . . . w n n ) ( x 1 ( t ) x 2 ( t ) . . . x n ( t ) ) + ( b 1 b 2 . . . b n ) ) − 1 2 ( 0 , 0 , . . . , Δ x j ( t ) , . . . , 0 ) ( w 11 w 12 . . . w 1 n w 21 w 22 . . . w 2 n . . . . . . . . . . . . w n 1 w n 2 . . . w n n ) ( 0 . . . Δ x j ( t ) . . . 0 ) = − ( Δ x j ( t ) w j 1 , Δ x j ( t ) w j 2 , . . . , Δ x j ( t ) w j n ) ( x 1 ( t ) x 2 ( t ) . . . x n ( t ) ) − Δ x j ( t ) b j − 1 2 ( Δ x j ( t ) w j 1 , Δ x j ( t ) w j 2 , . . . , Δ x j ( t ) w j n ) ( 0 . . . Δ x j ( t ) . . . 0 ) = − Δ x j ( t ) ∑ i = 1 n w j i x i ( t ) − Δ x j ( t ) b j − 1 2 Δ x j 2 ( t ) w j j = − Δ x j ( t ) [ ∑ i = 1 n w i j x i ( t ) + b j ] \begin{aligned}\Delta E(t) &=-(0,0,...\Delta x_j(t),...,0)\big(\begin{pmatrix} w_{11}& w_{12} &...& w_{1n}\\w_{21} & w_{22} &...&w_{2n}\\ ...&...&...&...\\ w_{n1} &w_{n2} &...& w_{nn}\end{pmatrix} \begin{pmatrix} x_1(t)\\x_2(t)\\...\\x_n(t)\end{pmatrix}+\begin{pmatrix} b_1\\b_2\\...\\b_n\end{pmatrix}\big)-\frac{1}{2}(0,0,...,\Delta x_j(t),...,0)\begin{pmatrix} w_{11}& w_{12} &...& w_{1n}\\w_{21} & w_{22} &...&w_{2n}\\ ...&...&...&...\\ w_{n1} &w_{n2} &...& w_{nn}\end{pmatrix}\begin{pmatrix} 0\\...\\\Delta x_j(t)\\...\\0\end{pmatrix}\\ &=-(\Delta x_j(t)w_{j1}, \Delta x_j(t)w_{j2}, ..., \Delta x_j(t)w_{jn})\begin{pmatrix} x_1(t)\\x_2(t)\\...\\x_n(t)\end{pmatrix}-\Delta x_j(t)b_j-\frac{1}{2}(\Delta x_j(t)w_{j1}, \Delta x_j(t)w_{j2}, ..., \Delta x_j(t)w_{jn})\begin{pmatrix} 0\\...\\\Delta x_j(t)\\...\\0\end{pmatrix}\\ &=-\Delta x_j(t)\sum_{i=1}^{n}w_{ji}x_i(t)-\Delta x_j(t)b_j-\frac{1}{2}\Delta x_j^2(t)w_{jj}\\ &=-\Delta x_j(t)\big[\sum_{i=1}^{n}w_{ij}x_i(t)+b_j\big] \end{aligned}\\ ΔE(t)=−(0,0,...Δxj(t),...,0)(⎝⎜⎜⎛w11w21...wn1w12w22...wn2............w1nw2n...wnn⎠⎟⎟⎞⎝⎜⎜⎛x1(t)x2(t)...xn(t)⎠⎟⎟⎞+⎝⎜⎜⎛b1b2...bn⎠⎟⎟⎞)−21(0,0,...,Δxj(t),...,0)⎝⎜⎜⎛w11w21...wn1w12w22...wn2............w1nw2n...wnn⎠⎟⎟⎞⎝⎜⎜⎜⎜⎛0...Δxj(t)...0⎠⎟⎟⎟⎟⎞=−(Δxj(t)wj1,Δxj(t)wj2,...,Δxj(t)wjn)⎝⎜⎜⎛x1(t)x2(t)...xn(t)⎠⎟⎟⎞−Δxj(t)bj−21(Δxj(t)wj1,Δxj(t)wj2,...,Δxj(t)wjn)⎝⎜⎜⎜⎜⎛0...Δxj(t)...0⎠⎟⎟⎟⎟⎞=−Δxj(t)i=1∑nwjixi(t)−Δxj(t)bj−21Δxj2(t)wjj=−Δxj(t)[i=1∑nwijxi(t)+bj]
仔细观察上式, ∑ i = 1 n w i j x i ( t ) + b j \sum_{i=1}^{n}w_{ij}x_i(t)+b_j ∑i=1nwijxi(t)+bj即为 j j j神经元的输入,则对应输出为:
x j ( t + 1 ) = { 1 , 当 ∑ i = 1 n w i j x i ( t ) + b j ≥ 0 − 1 , 当 ∑ i = 1 n w i j x i ( t ) + b j < 0 x_j(t+1)=\begin{cases} 1, 当\sum_{i=1}^{n}w_{ij}x_i(t)+b_j\ge0\\ -1,当\sum_{i=1}^{n}w_{ij}x_i(t)+b_j<0 \end{cases} xj(t+1)={ 1,当∑i=1nwijxi(t)+bj≥0−1,当∑i=1nwijxi(t)+bj<0
分情况讨论 x j ( t ) x_j(t) xj(t)和 x j ( t + 1 ) x_j(t+1) xj(t+1):
(1)若 x j ( t + 1 ) = x j ( t ) x_j(t+1)=x_j(t) xj(t+1)=xj(t), 则 Δ x j ( t ) = 0 \Delta x_j(t)=0 Δxj(t)=0, 故此时 Δ E ( t ) = 0 \Delta E(t)=0 ΔE(t)=0;
(2)若 x j ( t + 1 ) = − 1 , x j ( t ) = 1 x_j(t+1)=-1,x_j(t)=1 xj(t+1)=−1,xj(t)=1, 则 ∑ i = 1 n w i j x i ( t ) + b j < 0 \sum_{i=1}^{n}w_{ij}x_i(t)+b_j<0 ∑i=1nwijxi(t)+bj<0, 且 Δ x j ( t ) = − 2 < 0 \Delta x_j(t)=-2<0 Δxj(t)=−2<0,所以 Δ E ( t ) < 0 \Delta E(t)<0 ΔE(t)<0;
(3)若 x j ( t + 1 ) = 1 , x j ( t ) = − 1 x_j(t+1)=1,x_j(t)=-1 xj(t+1)=1,xj(t)=−1, 则 ∑ i = 1 n w i j x i ( t ) + b j ≥ 0 \sum_{i=1}^{n}w_{ij}x_i(t)+b_j\ge0 ∑i=1nwijxi(t)+bj≥0, 且 Δ x j ( t ) = 2 > 0 \Delta x_j(t)=2>0 Δxj(t)=2>0,所以 Δ E ( t ) ≤ 0 \Delta E(t)\le0 ΔE(t)≤0。
以上三种情况包含了所有可能的情况。因此,若以串行异步方式调整网络,而且连接矩阵为对称阵 w i j = w j i w_{ij}=w_{ji} wij=wji,无自反馈 w i i = 0 w_{ii}=0 wii=0, 则总有 Δ E ≤ 0 \Delta E\le0 ΔE≤0,即网络总数向能量函数减小方向演化,而能量函数有下界,因此最终一定能达到某个平衡点。
- 同步更新方式收敛证明:
在某时刻t, 所有神经元状态都产生变化,对于离散Hopfield网络,如果采用并行运行方式,且连接矩阵为非负定对称矩阵(即为半正定矩阵,不熟悉的可回去看下线代),则对于任意一个初态,系统都能稳定收敛到某个吸引子:
这里沿用上文的变量定义,有:
Δ E ( t ) = − 1 2 X T ( t + 1 ) W X ( t + 1 ) − X T ( t + 1 ) B + 1 2 X T ( t ) W X ( t ) + X T ( t ) B = − 1 2 ( X ( t ) + Δ X ( t ) ) T W ( X ( t ) + Δ X ( t ) ) − ( X ( t ) + Δ X ( t ) ) T B + 1 2 X T ( t ) W X ( t ) + X T ( t ) B = ( − 1 2 X T ( t ) W X ( t ) − 1 2 X T ( t ) W Δ X ( t ) − 1 2 Δ X T ( t ) W X ( t ) − 1 2 Δ X T ( t ) W Δ X ( t ) + 1 2 X T ( t ) W X ( t ) ) + ( X T ( t ) B − ( X ( t ) + Δ X ( t ) ) T B ) = − Δ X T ( t ) W X ( t ) − 1 2 Δ X T ( t ) W Δ X ( t ) − Δ X T ( t ) B = − Δ X T ( t ) [ W X ( t ) + B ] − 1 2 Δ X T ( t ) W Δ X ( t ) \begin{aligned}\Delta E(t) &=-\frac{1}{2}X^T(t+1)WX(t+1)-X^T(t+1)B+\frac{1}{2}X^T(t)WX(t)+X^T(t)B\\ &=-\frac{1}{2}(X(t)+\Delta X(t))^TW(X(t)+\Delta X(t))-(X(t)+\Delta X(t))^TB+\frac{1}{2}X^T(t)WX(t)+X^T(t)B\\ &=\big(-\frac{1}{2}X^T(t)WX(t)-\frac{1}{2}X^T(t)W\Delta X(t) -\frac{1}{2}\Delta X^T(t)WX(t) -\frac{1}{2}\Delta X^T(t)W\Delta X(t)+\frac{1}{2}X^T(t)WX(t)\big)+\big(X^T(t)B-(X(t)+\Delta X(t))^TB\big)\\ &=-\Delta X^T(t)WX(t)-\frac{1}{2} \Delta X^T(t)W\Delta X(t)-\Delta X^T(t)B\\ &=-\Delta X^T(t)[WX(t)+B]-\frac{1}{2} \Delta X^T(t)W\Delta X(t) \end{aligned} ΔE(t)=−21XT(t+1)WX(t+1)−XT(t+1)B+21XT(t)WX(t)+XT(t)B=−21(X(t)+ΔX(t))TW(X(t)+ΔX(t))−(X(t)+ΔX(t))TB+21XT(t)WX(t)+XT(t)B=(−21XT(t)WX(t)−21XT(t)WΔX(t)−21ΔXT(t)WX(t)−21ΔXT(t)WΔX(t)+21XT(t)WX(t))+(XT(t)B−(X(t)+ΔX(t))TB)=−ΔXT(t)WX(t)−21ΔXT(t)WΔX(t)−ΔXT(t)B=−ΔXT(t)[WX(t)+B]−21ΔXT(t)WΔX(t)
上述推导依然不变。
下面将上式的左右两半边分开证明:
(1)左半边:
− Δ X T ( t ) [ W X ( t ) + B ] = − ( Δ x 1 ( t ) , Δ x 2 ( t ) , . . . Δ x n ( t ) ) ( ( w 11 w 12 . . . w 1 n w 21 w 22 . . . w 2 n . . . . . . . . . . . . w n 1 w n 2 . . . w n n ) ( x 1 ( t ) x 2 ( t ) . . . x n ( t ) ) + ( b 1 b 2 . . . b n ) ) = − ( Δ x 1 ( t ) , Δ x 2 ( t ) , . . . Δ x n ( t ) ) ( ∑ i = 1 n w 1 i x i ( t ) + b 1 ∑ i = 1 n w 2 i x i ( t ) + b 2 . . . ∑ i = 1 n w n i x i ( t ) + b n ) = ∑ j = 1 n [ − Δ x j ( t ) ( ∑ i = 1 n w i j x i ( t ) + b j ) ] \begin{aligned} -\Delta X^T(t)[WX(t)+B] &=-(\Delta x_1(t),\Delta x_2(t),...\Delta x_n(t))\big(\begin{pmatrix} w_{11}& w_{12} &...& w_{1n}\\w_{21} & w_{22} &...&w_{2n}\\ ...&...&...&...\\ w_{n1} &w_{n2} &...& w_{nn}\end{pmatrix} \begin{pmatrix} x_1(t)\\x_2(t)\\...\\x_n(t)\end{pmatrix}+\begin{pmatrix} b_1\\b_2\\...\\b_n\end{pmatrix}\big)\\ &=-(\Delta x_1(t),\Delta x_2(t),...\Delta x_n(t))\begin{pmatrix} \sum_{i=1}^{n}w_{1i}x_i(t)+b_1\\\sum_{i=1}^{n}w_{2i}x_i(t)+b_2\\...\\\sum_{i=1}^{n}w_{ni}x_i(t)+b_n\end{pmatrix}\\ &=\sum_{j=1}^{n}\big[-\Delta x_j(t)(\sum_{i=1}^{n}w_{ij}x_i(t)+b_j)\big] \end{aligned} −ΔXT(t)[WX(t)+B]=−(Δx1(t),Δx2(t),...Δxn(t))(⎝⎜⎜⎛w11w21...wn1w12w22...wn2............w1nw2n...wnn⎠⎟⎟⎞⎝⎜⎜⎛x1(t)x2(t)...xn(t)⎠⎟⎟⎞+⎝⎜⎜⎛b1b2...bn⎠⎟⎟⎞)=−(Δx1(t),Δx2(t),...Δxn(t))⎝⎜⎜⎛∑i=1nw1ixi(t)+b1∑i=1nw2ixi(t)+b2...∑i=1nwnixi(t)+bn⎠⎟⎟⎞=j=1∑n[−Δxj(t)(i=1∑nwijxi(t)+bj)]
而在异步更新的证明中,实际上已经证明了,对于任何一个要更新的神经元 j j j, 都有 − Δ x j ( t ) [ ∑ i = 1 n w i j x i ( t ) + b j ] ≤ 0 -\Delta x_j(t)[\sum_{i=1}^{n}w_{ij}x_i(t)+b_j] \le0 −Δxj(t)[∑i=1nwijxi(t)+bj]≤0, 对所有神经元求和,依然会 ≤ 0 \le0 ≤0, 左半边证毕。
(2)右半边:
为证 − 1 2 Δ X T ( t ) W Δ X ( t ) ≤ 0 -\frac{1}{2} \Delta X^T(t)W\Delta X(t)\le0 −21ΔXT(t)WΔX(t)≤0, 考虑到矩阵 W W W为非负正定矩阵,直接利用非负正定矩阵(一般叫半正定矩阵)性质:
u T W u ≥ 0 u^TWu\ge0 uTWu≥0对所有非0向量 u u u成立。直接得证。
综上得,同步并行算法,依然满足 Δ E ( t ) ≤ 0 \Delta E(t)\le 0 ΔE(t)≤0。从上面可以看到,当网络的能量始终向减小方向演变,当能量最终稳定于一个常数时,该常数对应网络能量的极小状态,称该网络的极小状态为能量井,能量井对应网络的吸引子。
玻尔兹曼分布:
参照:
(1)
(2)
(3)
玻尔兹曼分布Boltzmann distribution(又叫Gibbs Distribution),本是热力学和统计学分布,但在量子力学和机器学习领域也得到广泛应用。
在决策树章节,引入了熵,
然后引入最大熵原理:
有些随机事件往往不可能直接计算,平常对具体问题做处理时,掌握的仅仅是一些与随机事件有关的随机变量的统计平均值,以及某些其他制约条件。而当一个随机变量平均值给定时,可以有多种概率分布与之相容。如何挑选出“最可几”的分布作为实际分布,要做到这点,最大熵原理可作为挑选标准。(最可几分布Most Probable Distribution, 或最概然分布。表示在特定系统的特定状态下,出现概率最大的分布。实际上并不是某种具体的分布,而更像符合某一特定目标的分布。)
最大熵原理,主要思想是,在只掌握关于未知分布的部分知识时,应该选取符合这些知识且熵值最大的概率分布。其实质就是,在已知知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断(也就是说已知的一定要满足,未知的不去过多臆测,而是认为平均分布),这是一个唯一不偏不倚的选择。任何其他的选择都意味着增加了其他的约束和假设,这些约束和假设根据我们掌握的信息无法做出。
数学分析如下:
设实验有 n n n种状态(结果),含 M M M个随机变量。
下面先寻找其约束条件(即已知条件):
(1) 第 j j j个随机变量 f ( j ) f^{(j)} f(j)的期望(或统计均值) F j F_j Fj可由实验得知,且知期望公式:
F j = ∑ i = 1 n f i ( j ) p i F_j=\sum_{i=1}^n f_i^{(j)}p_i Fj=i=1∑nfi(j)pi
其中 f i ( j ) f_i^{(j)} fi(j)表示系统在状态 i i i时,第 j j j个随机变量的对应取值。一共有 M M M个变量,所以有 M M M个等式(约束);
(2) 系统各个状态概率满足归一化条件:
∑ i = 1 n p i = 1 \sum_{i=1}^np_i=1 i=1∑npi=1
根据以上两个约束(实际上是 M + 1 M+1 M+1个约束),用Lagrange乘子法求最大熵 H ( X ) H(X) H(X)(构造凸函数,求 − H ( x ) -H(x) −H(x)最小值):
J ( p i ) = − H ( X ) + α ( ∑ i = 1 n p i − 1 ) + ∑ j = 1 M β j ( ∑ i = 1 n f i ( j ) p i − F j ) = ∑ i = 1 n p i ln p i + α ( ∑ i = 1 n p i − 1 ) + ∑ j = 1 M β j ( ∑ i = 1 n f i ( j ) p i − F j ) \begin{aligned} J(p_i) &=-H(X)+\alpha (\sum_{i=1}^np_i-1)+\sum_{j=1}^M \beta_j(\sum_{i=1}^n f_i^{(j)}p_i-F_j)\\ &=\sum_{i=1}^np_i \ln p_i+\alpha (\sum_{i=1}^np_i-1)+\sum_{j=1}^M \beta_j(\sum_{i=1}^n f_i^{(j)}p_i-F_j) \end{aligned} J(pi)=−H(X)+α(i=1∑npi−1)+j=1∑Mβj(i=1∑nfi(j)pi−Fj)=i=1∑npilnpi+α(i=1∑npi−1)+j=1∑Mβj(i=1∑nfi(j)pi−Fj)
对 p i p_i pi求导得:
∂ J ( p i ) ∂ p i = ln p i + 1 + α + ∑ j = 1 M β j f i ( j ) \frac{\partial J(p_i)}{\partial p_i}=\ln p_i+1+\alpha+\sum_{j=1}^M\beta_jf_i^{(j)} ∂pi∂J(pi)=lnpi+1+α+j=1∑Mβjfi(j)
令上式为0, 可得:
p i = e x p ( − 1 − α − ∑ j = 1 M β j f i ( j ) ) p_i=exp(-1-\alpha-\sum_{j=1}^M\beta_jf_i^{(j)}) pi=exp(−1−α−j=1∑Mβjfi(j))
这就是一般情况下最大熵公式。
接下来引入推导玻尔兹曼分布:
设一个由 N N N( N N N很大)个微观粒子组成的近独立体系,体系总能量E等于各个粒子能量和。通常围观粒子的状态和能量是量子化的,每一个能级上又具有若干个量子态,如下:
单粒子状态编号: 1 , 2 , . . . N 1,2,...N 1,2,...N, 共有 N N N个粒子;
能级: E 1 , E 2 , . . . E n E_1, E_2,...E_n E1,E2,...En,共有 n n n个能级;
量子态数: g 1 , g 2 , . . . g n g_1, g_2,...g_n g1,g2,...gn, 能级 E j E_j Ej上,有 g j g_j gj个量子态数。
总量子态数: m = g 1 + g 2 + . . . + g n m=g_1+g_2+...+g_n m=g