机器学习基础回顾
序言 ----为了巩固一下之前的知识,最近重温了下西瓜书和统计学习方法,所以顺带写篇博客。
一、什么是机器学习,即机器学习的定义。
我认为可以从广义和狭义上去说,
广义上说就是让机器具有类似人一样的学习能力,通过学习新知识来提高自己的能力,而非直接编程告诉机器每一步执行什么。
狭义上说,就是让计算机基于数据构建(概率统计)模型,并通过该模型对未知数据进行预测与分析的方法。
(西蒙曾对“学习”下过这么一个定义:如果一个系统能够通过执行某个过程改进它的性能,这就是学习)
总结性的话说,机器学习研究的是数据,识别或总结出数据中的规律,构建模型。而它目的是对未知数据做预测,可以通过训练能够提升预测的准确度
二、有了定义,那么机器学习又可以分为哪些类呢?
常见的分类有:监督学习、无监督学习、强化学习
监督学习是我们最为常见的情况,它又可以分为回归问题、分类问题和标注问题。
输入和输出都是连续的值则是回归问题。输出是离散值则为分类问题。
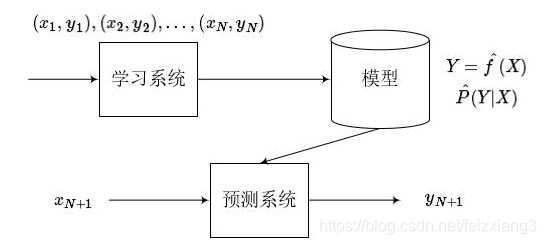
下图监督学习的过程图,首先基于训练数据学习一个模型,然后再用该模型对测试集做预测。
模型一般有两种表示方法,决策函数(输入X,得到结果Y),或者 条件概率分布(已知X得到Y的概率)
那么模型又分为哪些类型呢?
根据决策函数是否是线性函数,可以分为线性模型和非线性模型。
感知机、线性回归、线性支持向量机、k近邻 k均值等都是线性模型
核函数支持向量机、决策树、神经网络都是非线性模型
根据生产方法的不同,又可以分为生产模型和判别模型
由数据学习联合概率分布P(X,Y)然后求出条件概率分布P(Y|X)作为预测模型,即生成模型。典型的生成模型有朴素贝叶斯 、隐马尔科夫模型。
由数据直接学习决策函数或条件概率分布作为预测的模型,即判别模型。包括k邻近 、感知机、决策树、逻辑回归、最大熵模型、支持向量机、条件随机场等。
我们已经知道,模型由决策函数或条件概率分布的形式给出,同时它也可以理解为由输入空间到输出空间的映射,而这些映射的集合成为假设空间。
那么下面的问题是,怎么从假设空间中找到最佳的映射,或者称找到最佳的模型,使得模型的预测最为准确。
为了解决这个问题,我们要评价模型的好坏,于是引入了损失函数、风险函数的概念。损失函数是度量模型一次预测的好坏。风险函数是度量整体样本的 平均意义下的模型的好坏。
常见的损失函数有 0-1损失 绝对值损失 平方损失 对数损失 。本质都是对比模型的估计值y_hat与标记值y 来衡量模型的好坏。当然,损失函数的值越小,模型的越好。因此我们把问题转换为使经验风险最小化的,最优化问题。通过最小化经验风险得到参数theta的值,从而得到最优的模型。
最小化的过程,又涉及到了梯度下降算法,这里不再展开讲。
三、过拟合、数据集的划分 和 模型的评估
首先解释一个重要概念,过拟合。
我们知道,模型是通过我们在已有的训练数据上不断训练学习到的,但模型好坏最终的评判是在测试集上,模型对未知数据的预测能力成为泛化能力。 当模型过于复杂比如参数过多时,会出现模型对已知数据预测的很好,但对未知数据预测的很差的情况,这就称为过拟合。我们要尽可能减少过拟合,提升模型的泛化能力。
另外一种偏口语化的理解方式是,模型越复杂它的学习能力就会越强,当它过于复杂时,它就会过分的在训练数据中追求极致,以至于把训练集的误差都当做是特征给学习了。当遇到一个新问题,它很可能没法给出好的答案,因为之前的学习方法错了,它也许能给出一个好答案,也许会给出一个错的很离谱的答案,因为它学到的模型把误差考虑了进去,经过不断放大,结果可想而知。
相应的概念还有欠拟合,顾名思义,模型过于简单,即使再怎么训练也无法较好的对数据拟合做出预测,这种情况一般我们只要提高模型的复杂度即可。
提升模型的泛化能力,一般有两种方法:
第一是增加训练样本,但这种方法不是很实用,很多时候数据集很难收集,只能在有限的数据集上去操作。
第二,经验风险加上正则化项,从而在迭代过程中,控制模型的复杂度。
常见的正则化项,包括 L1范数、L2范数 Dropout等
L1正则化是指权值向量w 中各个元素的绝对值之和
L2正则化是指权值向量w 中各个元素的平方和然后再求平方根
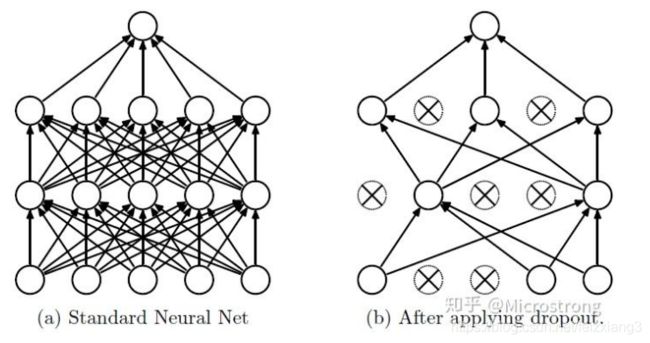
Dropout主要是用在 人工神经网络中,简单的解释:当数据在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征。 这个过程看下图
最后提一下奥姆剃刀原理在模型选择上的解释:在所有可能的选择中,能够很好的解释已知数据并且十分简单的模型才是最好的模型。 通俗一点理解就是,如果你要杀死一只鸟,给你两个选择,1是鸟枪,2是原子弹。你会选择哪个? 很明显这两个选择都完全可以满足你的目的,但原子弹显然要比鸟枪复杂的多,同时也危险的多,它杀死鸟的同时还会杀死无数的其它生物。而你想要的只不过是打个鸟而已。你并不想毁灭这个世界。
接下来要说的是数据集的划分,这是一个很实际的问题。
通常我们会把数据集分成两部分,一部分称为训练集,用于模型训练,一部分称为测试集,用来验证模型的选择。
如果数据量非常充足,我们可以简单的使用留出法,即划分两个互斥的子集,常见的比例有8:2 、7:3
另外最常见的划分方法是s折交叉验证。即把数据划分为S等分,取其中S-1份为训练集,剩余一份做测试集,去训练模型。将这一过程对可能的S中选择重复进行,最后选出S次测评中误差最小的模型。
作为S折交叉验证的特例,留一交叉验证,它的评估结果是最准确的,但是它的缺陷是数据集比较大时,要训练太多的模型,计算开销是无法忍受的。
当数据量较小,难以有效划分训练集和测试集时,可以使用自助法。所谓自助法,就是有放回的采样。每次从数据中采样一个样本加入训练集,然后把它放回数据集,重复这一过程m次,这样就得到一个样本大小为m的训练集。显然有一部分样本会在训练集中重复出现多次,这样做的缺点是,它改变了数据集的初始数据分布,会引入估计误差。
最后我想说下,模型的评估指标
这里讨论下分类问题的评估指标
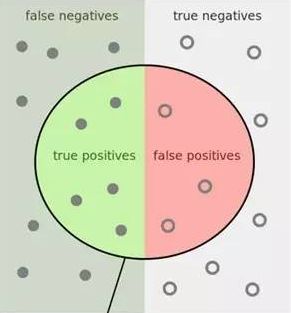
首先引入一张经典图片:
如上图,整张图片中的点是所有测试集数据。
数据分成了四部分:
TP : True Positive 真正例
FP : False Positive 假正例
FN: False Negative 假负例
TN: True Negative 真正例
有以下几个常用指标:
ACC 即准确率 accuracy ; acc = (TP +TN ) / (TP + FP +TN +FN) 即 预测正确的样本数占整体样本数的比例。
精准率(Precision) P = TP / (TP+FP) 即你预测所有正样本中真的是正样本的比例。
召回率(Recall) R = TP / (TP + FN) 即所有正样本中你预测出来的正样本的比例(确实有点召回的意思)。
上述三个指标都能一定程度上评估模型的好坏,但都存在一定的问题。
当数据类别不平衡的时候,比如一个预测垃圾邮件的任务,如果1000封邮件中只存在10封垃圾邮件,如果你的模型是把所有邮件都判断为正常邮件,那么你的准确率仍高达99%但其实你的模型没有任何卵用。
这是,上面例子的 召回率 R = 0% 貌似召回率还挺靠谱的
但看下面的例子,还是1000封邮件中只存在10封垃圾邮件,但你的模型预测,直接把所有邮件都判断为垃圾邮件。
那么 召回率R = 100% ,但模型仍然没有卵用。这时精准率为1%,看起来这个指标比较靠谱,但看下面的例子
10000个肿瘤样例,里面有10个是恶性的。 模型的预测 10个中有9个预测正确,另外9990个良性中把10个预测为恶性。
那么 P = 9 /(9+10) = 47.37% 分数并不高 而其实这样的成绩已经相当好了,召回率 R = 90% 准确率ACC = 0.9989
从上面的例子可以看出,上面三个指标,当遇到类别不平衡的数据时,如果单看一个指标都有可能对模型评估出现偏差。
所以有了下面的 F-SCORE
其中最常见的是 F1-score 即 上式中β = 1时 ,f1 = 2 * P*R / (P+R) 它是综合考虑了召回率和精准率,值在0到1之间。
另外当β小于1时,分数的权重更偏向于 Precision 当β大于1时,分数的权重偏向于 Recall
最后还有一个很重要的二分类模型评价指标 ---ROC曲线 和 AUC值
如图所示ROC曲线,纵坐标是TPR 横坐标是FPR
TPR = TP/(TP+FN)
FPR = FP/(FP + TN)
那么这条曲线是怎么画出来的呢?
以逻辑回归为例,每个测试样本,可以有一个0到1的输出值,代表为正样本的概率。我们把所有样本按为正样本的概率从大到小排序。这样最有可能为正例的样本排在最前,最不可能是正例的排在最后。
接下来,我们从高到低,依次将概率值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。这样,每次我们就可以得到一组FPR和TPR,即ROC曲线上的一点。最终所有测试数据画出一个点,连接所有点就是ROC曲线。
AUC 是ROC曲线下面的面积,AUC的值在 0.5~1之间
一般来说,如果ROC是光滑的,那么基本可以判断没有太大的overfitting,AUC面积越大一般认为模型越好。
为什么使用ROC曲线
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。