强化学习之Q-learning算法实战1

实战内容：

1、一维探宝

2、二维探宝

 

所需环境：pycharm

所需安装包：graphic、numpy、pandas、gym

 

 

一、实际效果：

一维探宝：

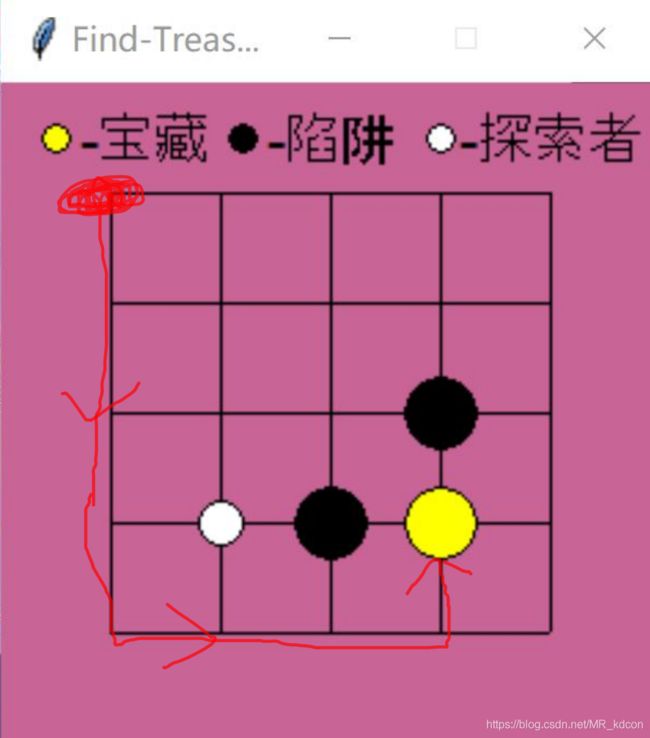
二维探宝：

二维探宝升级版：

 

 

二、Q-learning算法：

输入：

     环境E：用于对机器人做出的动作进行反馈，反馈当前奖励r（本设计中，规定拿到宝藏才有奖励，落入陷阱获得负奖励，其余无奖励）与下个状态state'。如实际效果中的横向轴与棋盘

     动作空间A：一维中['left', 'right']；二维中[‘up’, 'down', 'left', 'right']

     奖赏折扣：Q-learning一般使用折扣累计奖赏，利用动态规划，用状态-动作值函数Q做决策，是个对每一步奖赏进行衰减的一个0-1之间的常数，我设为0.9

     更新步长：也可以说学习率，0-1之间的常数，我设为0.01

     尝试概率：Q-learning会采用-greedy策略去选取动作，0-1之间的值，我设为0.1，也就是10%的概率随机在动作空间A中随机选取动作，90%的概率选取当前最优动作，即aciton* = argmax Q(s,a)

过程：

     1、初始化动作-状态值函数为pandas表格，index为各个状态，column为动作空间，内容为0；初始化状态s0；随机抽取动作

     2、for t=1,2,3...do

     3、    r,s' = 在E中执行动作a（a由-greedy策略对当前状态s产生）后产生环境回馈的当前奖励和下个状态。

     4、    选择最优策略选出s'状态下的动作a'。

     5、    更新Q表：Q（s，a） +=  * （r +  * Q（s'，a'） - Q（s，a））

     6、    更新s = s'，输出策略a'' = argmax Q(x, a'')存于Q表中

     7、end for

     8、最后Q表中的值就是输出的策略policy，通过这个策略，机器人可以以最快速度找到宝藏

 

note：

1、一维中的状态为x轴点的值0-4，以及宝藏‘end’；二维中为22个点的坐标（x,y）以及陷阱的2个坐标和宝藏‘end’坐标

2、很多Q-learning算法中将4、5两步合并成Q（s，a） +=  * （r +  * max Q（s'） - Q（s，a）），其实是一样的。

3、当s'=宝藏或者陷阱的时候，Q（s'，a'）= 0，因为值函数Q的含义是，在s'状态下，执行a'动作后获得的累积奖励，而找到宝藏和落入陷阱不会执行任何动作，所以没有值。

4、-greedy策略在实际编程过程中，要用的argmax，这个函数在当存在多个值相同时，会选取索引最前面的那个动作，为了避免这个，我们需要在几个相同最大值的动作中进一步随机选取。

5、以一维寻宝 为例，第一次尝试成功后，经过努力最终产生一个策略（即Q表），但这个策略并不好用，此时Q中只有拿到宝藏前那个状态_s才有值，而其余均为初始化的0。接下来的尝试中，机器人会向无头苍蝇一样到处乱走，花很久才收敛，第二次尝试成功       后，走到 _s前的那个状态__s也会有一个合理的值，其实在__s状态下，由于_s的max特点，会诱导机器人走向_s，而不是往另一个方向走，从而走向宝藏，加快了收敛，这样就是为什么越是训练到后面，机器人寻宝速度越快的原因！因此，接下来的尝试中，       Q表中的值会由最后一个状态_s出发，一个个计算出Q表中的其他值，加快收敛，最终形成policy。

6、实际中会发现，在找到最佳策略policy后，机器人偶尔也会“走下弯路”，就是说会比最佳策略还要收敛慢一点。那是因为机器人不完全是按使Q表最大下的最优动作执行的，这是因为-greedy策略有10%会随机选取动作。

7、实际中，需要在状态更新后加点延迟，这样看起来才有效果，不然飞速的执行，人的眼球跟不上的。。。

8、关于第五行Q值的更新原理：Q-learning是基于值迭代算法的，因此r +  * Q（s'，a'）表示target Q，即目标Q值，因此Q-learning算法就需要让下时刻的Q（s,a）无线靠近它，因此采用了一种类似梯度下降的算法，让Q（s,a）每次一小步（步伐取决于学习率lr）不断靠近target Q，最后达到收敛。

 

 

 

三、代码解析：

一维：

Q-lerning类

class Qlearning(object):
    def __init__(self):
    用于规定输入的参数以及Q表
    def choose_action(self, s):
    用-greedy策略选取动作
    def return_back_env(self, a, s):
    得到环境的反馈r、s'
    def q_table_update(self, s, a, s_, r):
    算法第5步，更新Q表
    def update_env(self, S, episode, step_counter):
    更新环境，实时显示状态变化

主函数：描述Q-learning算法

def rl_train():
    ql = rl.Qlearning()  # Q-learning算法例化
    for epoch in range(ql.epochs):  # 训练回合
        s = 0  # 初始化状态
        step_counter = 0  # 记录一共用了几步收敛
        is_end = False  # 记录是否结束
        ql.update_env(s, epoch, step_counter)  # 更新环境
        while not is_end:
            a = ql.choose_action(s)  # 选择动作
            r, s_ = ql.return_back_env(a, s)  # 得到E的反馈
            if s_ == 'end':
                _, s = ql.q_table_update(s, a, s_, r)  # 更新Q表，并更新状态
                is_end = True
            else:
                _, s = ql.q_table_update(s, a, s_, r)
            step_counter += 1
            ql.update_env(s, epoch, step_counter)
    return ql.table  # 返回最终策略policy

 

二维：

这里用到了graphic包用于GUI，也可以用tkinter或者gym

用graphic创建棋盘环境E

Q-learning类：和一维差不多，只是要增加一个检查状态是否存在的函数，因为棋盘上状态很多，还有陷阱，无法一一罗列，因此创建空的Q表，遇到一个状态，经过检擦不在Q表内，就增加这个状态

class Qlearning(object):
    def __init__(self):
    规定输入的参数
    def choose_action(self, s):
    用-greedy策略选取动作
    def q_table_update(self, s, a, s_, r):
    Q表更新
    def check_exsit_state(self, state):
    检查状态是否存在Q表中

class Table():
    def __init__(self, width, height, grid_size,ql):
    初始化棋盘E一些参数
    def reset(self):  
    # 探索者复位，用于当落入陷阱或者找到宝藏回到原位继续训练
    def step(self, a):
    # 用于对环境做出反应，输出当前奖励r以及下个状态（这个函数在一维中是在Q-learning类中的因为环境也在那个类中，依赖于环境，所以放到了棋盘类中）

主函数：描述Q-learning算法

二维探宝
def fine_treasure():
    for epoch in range(50):
        s = table.reset()  # 复位

        while True:
            time.sleep(0.1)  # 更好的显示每一步的走路时间
            a = ql.choose_action(str(s))  # 选取动作
            r, s_, done = table.step(a)  # 得到反馈并更新环境
            _, s = ql.q_table_update(str(s), a, str(s_), r)  # 更新Q表

            if done:  # 遇到陷阱或者宝藏，开启下次探索
                break
    return ql.table  # 返回最终策略

if __name__ == '__main__':
    # width = 6;height = 6;size = 40  # GUI窗口大小
    # ql = rl.Qlearning()  # Q-learning算法函数类
    # table = tb.Table(width, height, size, ql)  # 棋盘类例化
    # q_table = fine_treasure()  # 执行Q-learning算法
    # print(q_table)  # 打印policy

 

 

 

四、inference

上述的训练过程得到了最终策略policy，那么接下来讲下机器人如何去利用这个自己摸索出来的最优policy呢？

接下来分别以一维和二维为例子：（二维是一样的道理，只是多了2个动作，状态从数值变成了坐标，还多了陷阱）

 

一维下：

初始状态s=0：

这是某次训练得到的Q表：

    left                     right
0  0.000000e+00  2.363961e-08
1  1.427087e-10  1.649183e-06
2  0.000000e+00  1.131456e-04
3  5.853488e-07  3.839580e-03
4  0.000000e+00  9.561792e-02
5  0.000000e+00  0.000000e+00

 

根据Q-learning算法（注意方便叙述，-greedy策略直接选用90%概率的最大Q值策略），首先根据-greedy策略，选取动作为 2.363961e-08对应的‘right’动作，向右并没有得到宝藏，所以r=0，s'=1，s'下对应的a'='right'，接下来更新Q表，然后s=s'=1.

然后下个回合继续：根据-greedy策略，选取动作为1.649183e-06对应的‘right’动作，向右并没有宝藏，所以r=0，s'=2，s'下对应的a'='right'，接下来更新Q表，然后s=s'=2.

然后下个回合继续：根据-greedy策略，选取动作为1.131456e-04对应的‘right’动作，向右并没有宝藏，所以r=0，s'=3，s'下对应的a'='right'，接下来更新Q表，然后s=s'=3.

然后下个回合继续：根据-greedy策略，选取动作为3.839580e-03对应的‘right’动作，向右并没有宝藏，所以r=0，s'=4，s'下对应的a'='right'，接下来更新Q表，然后s=s'=4.

然后下个回合继续：根据-greedy策略，选取动作为9.561792e-02对应的‘right’动作，向右得到宝藏，所以r=1，s'=‘end’，Q(s',a')直接为0，并更新Q表，然后s=s'='end'

结束一次探宝过程。

从Q表可以看出，策略使得left值和right的值相差不小，这样可以使得机器人更准确做出每一步的决策，随着不断地inference，策略会更加准确，但是从经验上看，收敛会变得缓慢，但是足以做出很好的决策了。

 

 

 

二维下：

初始状态（x,y）= （40，40），棋盘每个格子大小为40*40，窗口大小6*40*6*40，棋盘大小5*40*5*40

某次训练后的Q表，我们来分析看机器人会走啥路线

 

动作0：向上  1：向下  2：向左  3：向右     反馈：获取宝藏+2，落入陷阱-2，其余不给奖励

首先位于棋盘左上方，通过-greedy策略选取最大值对应的动作1，为向下走；获取环境的反馈为r=0，s'=（40，80），s'下的对应的a'为1，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作1，为向下走；获取环境的反馈为r=0，s'=（40，120），s'下的对应的a'为1，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作1，为向下走；获取环境的反馈为r=0，s'=（40，160），s'下的对应的a'为1，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作1，为向下走；获取环境的反馈为r=0，s'=（40，200），s'下的对应的a'为3，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作3，为向右走；获取环境的反馈为r=0，s'=（80，200），s'下的对应的a'为3，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作3，为向右走；获取环境的反馈为r=0，s'=（120，200），s'下的对应的a'为3，然后更新Q表，并更新s=s'。

 然后继续下个回合，通过-greedy策略选取最大值对应的动作3，为向右走；获取环境的反馈为r=0，s'=（160，200），s'下的对应的a'为0，然后更新Q表，并更新s=s'。

然后继续下个回合，通过-greedy策略选取最大值对应的动作0，为向上走；获取环境的反馈为r=0，s'=（160，160），s'=宝藏。游戏结束。

 

所以机器人走的路线是

最短路线：共8步。当然在其他训练过程中，还会出现其他8步的最短路线，但无论哪一条，都是最优路线8步。

对于升级版，也是同理，升级版中也使用了陷阱，还增加了墙壁障碍（黑色为Agent，黄色为宝藏）：

结果如下：

从上图看出，Agent在400个episode之后就达到收敛，Q-learning对离散状态、离散动作下的RL任务收敛效果很不错！

 

 

五、总结：

可以看粗一维到二维增加的难度来源于状态、动作的增多，随着环境的复杂恶劣，会有许多状态，因此Q表的存储和查询就相对不那么让人满意，因此接下来就会出现DQN，deep Q-learning network，加入了深度网络进行处理。

参考莫烦强化学习：https://www.bilibili.com/video/BV13W411Y75P