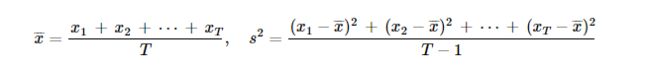https://github.com/hym105289/Percolation
1. 基本介绍
1.作业地址:http://coursera.cs.princeton.edu/algs4/assignments/percolation.html
2.模型介绍
①有一个N-by-N矩阵,如上图,每个小格子代表一个site
②当site为black时说明当前site为blocked(关闭的)
③非黑色为open
④当一个site为open且他和其他相邻的site连接并且可以连接到矩阵顶部我们称这个site为full
⑤如果矩阵最底部有site可以连接到矩阵顶部,我们称这个矩阵为渗透的
3. 作业要求
每个site以概率p为open,1-p的概率阻塞,计算当概率多少时系统是渗透的?
4. 基本思路
假设要测试20*20的系统以概率多少能渗透,比如每次随机地选择一个site设置成open,当系统渗透时有204个site是open的,那么p=204/400=0.51.我们需要做的就是反复试验计算p的值。
2. 判断系统是否是渗透?
1.数据结构
public class Percolation {
private WeightedQuickUnionUF grid;//保存连通的信息
private boolean[] state;//保存每个site是否open
private final int n;
public Percolation(int n) // create n-by-n grid, with all sites blocked
public void open(int row, int col) // open site (row, col) if it is not open already
public boolean isOpen(int row, int col) // is site (row, col) open?
public boolean isFull(int row, int col) // is site (row, col) full?
public int numberOfOpenSites() // number of open sites
public boolean percolates() // does the system percolate?
public static void main(String[] args) // test client (optional)
}
2.如何进行Open操作
①[row,col]当前的state为true,则已经open了则直接返回
②[row,col]当前的state为false,先将state设置为true,然后判断相邻的上下左右四个点是否是open的,如果是open的就将其进行连接。注意:每次都要检测row和col的合法性质,下标从1开始。
2.如何进行isFull操作
①首先判断[row,col]isOpen,如果false直接返回false;
②for 第一行的第一列 to 第一行的最后一列:先判断是否isOpen,如果false,直接返回false;如果是open的那么就继续判断[row,col]和该点是不是connected,如果是则返回true,否则返回false;
3.反复进行实验,计算概率p
①首先初始化一个N-by-N矩阵,全部为blocked。
②重复以下动作直到这个矩阵渗透为止:从blocked状态的sites中随机选择一个site将其open,直到当前模型渗透为止。
③然后计算open状态的sites的个数设为number,利用number/(N*N)计算出渗透率。
假设进行T次实验,每次求得阈值为x,则有:
利用标准差和平均值思想找出置信率为95%的阀值:
public class PercolationStats {
private final double[] threshold;
private double x;
private double s;
public PercolationStats(int n, int trials) // perform trials independent experiments on an n-by-n grid
public double mean() // sample mean of percolation threshold
public double stddev() // sample standard deviation of percolation threshold
public double confidenceLo() // low endpoint of 95% confidence interval
public double confidenceHi() // high endpoint of 95% confidence interval
public static void main(String[] args) // test client (described below)
}
总结
1.要注意row和col的取值范围都是1-n,并不是我们通常的从0开始索引。
2.一定要记得判断row和col的合法性质
3.StdRandom.uniform(lo,hi)产生的是从lo到hi-1的随机数
4.代码:
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.WeightedQuickUnionUF;
public class Percolation {
private WeightedQuickUnionUF grid;
private boolean[] state;
private final int n;
public Percolation(int n) {
if (n <= 0) {
throw new IllegalArgumentException();
} else {
this.n = n;
int size = this.n * this.n + 1;
grid = new WeightedQuickUnionUF(size);
state = new boolean[size];
for (int i = 1; i < size; i++) {
state[i] = false;
}
}
}
private boolean isInGrid(int i, int j) {
if ((i < 1 || i > n) || (j < 1 || j > n))
return false;
else
return true;
}
public void open(int row, int col) {
if (!isInGrid(row, col)) {
throw new IllegalArgumentException();
}
if (isOpen(row, col))
return;
int p = (row - 1) * this.n + col;
state[p] = true;
int up = p - this.n;
if (isInGrid(row - 1, col) && state[up]) {
grid.union(p, up);
}
int left = p - 1;
if (isInGrid(row, col - 1) && state[left]) {
grid.union(p, left);
}
int right = p + 1;
if (isInGrid(row, col + 1) && state[right]) {
grid.union(p, right);
}
int bottom = p + this.n;
if (isInGrid(row + 1, col) && state[bottom]) {
grid.union(p, bottom);
}
}
public boolean isOpen(int row, int col) {
if (row < 1 || row > this.n || col < 1 || col > this.n) {
throw new IllegalArgumentException();
}
int index = (row - 1) * this.n + col;
return state[index];
}
public boolean isFull(int row, int col) {
if (row < 1 || row > this.n || col < 1 || col > this.n) {
throw new IllegalArgumentException();
}
int p = (row - 1) * this.n + col;
for (int i = 1; i < this.n + 1; i++) {
// first must consider the row,col is open
if (isOpen(1, i) && isOpen(row, col) && grid.connected(p, i))
return true;
}
return false;
}
public int numberOfOpenSites() {
int num = 0;
int size = this.n * this.n + 1;
for (int i = 0; i < size; i++) {
if (state[i])
num++;
}
return num;
}
public boolean percolates() {
int row = this.n;
for (int col = 1; col < this.n + 1; col++) {
if (isFull(row, col))
return true;
}
return false;
}
public static void main(String[] args) {
int[] test = new In(args[0]).readAllInts();
Percolation percolation = new Percolation(test[0]);
for (int i = 1; i < test.length - 2; i += 2) {
percolation.open(test[i], test[i + 1]);
System.out.println(
test[i] + "," + test[i + 1] + " isopen:" + percolation.isOpen(test[i], test[i + 1]));
System.out.println(
test[i] + "," + test[i + 1] + " isfull:" + percolation.isFull(test[i], test[i + 1]));
System.out.println(test[i] + "," + test[i + 1] + " percolation:" + percolation.percolates());
}
}
}
import edu.princeton.cs.algs4.StdRandom;
import edu.princeton.cs.algs4.StdStats;
public class PercolationStats {
private final double[] threshold;
private double x;
private double s;
public PercolationStats(int n, int trials) {
if (n <= 0 || trials <= 0) {
throw new IllegalArgumentException();
}
threshold = new double[trials];
for (int i = 0; i < trials; i++) {
Percolation p = new Percolation(n);
while (!p.percolates()) {
int row = StdRandom.uniform(1, n + 1);
int col = StdRandom.uniform(1, n + 1);
if (!p.isOpen(row, col)) {
p.open(row, col);
}
}
threshold[i] = (double) p.numberOfOpenSites() / n / n;
}
}
public double mean() {
x=StdStats.mean(threshold);
return x;
}
public double stddev() {
s=StdStats.stddev(threshold);
return s;
}
public double confidenceLo() {
double low = x - 1.96 * s / (Math.sqrt((double) threshold.length));
return low;
}
public double confidenceHi() {
double hi = x + 1.96 * s / (Math.sqrt((double) threshold.length));
return hi;
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
int trials = Integer.parseInt(args[1]);
PercolationStats stats = new PercolationStats(n, trials);
double x = stats.mean();
double s = stats.stddev();
double low = stats.confidenceLo();
double hi = stats.confidenceHi();
System.out.printf("mean=%f\n", x);
System.out.printf("stddev=%f\n", s);
System.out.printf("%f %f\n", low, hi);
}
}
http://blog.csdn.net/zerodshei/article/details/53504171