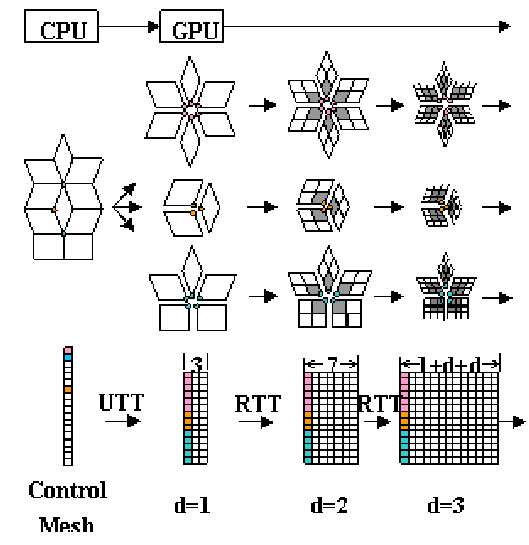
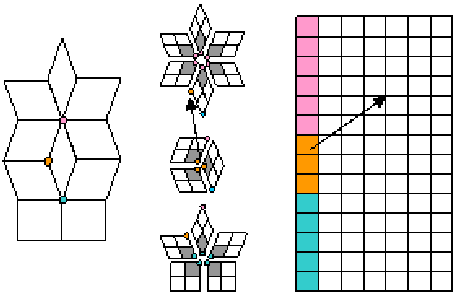细分曲面的GPU完全实现
细分曲面的GPU完全实现
张嘉华 梁成 李桂清
(华南理工大学计算机科学与工程学院 广东 广州 510640)
摘要:本文提出一种完全在GPU上实现的细分曲面绘制策略。该方法以扇区为基本单元,利用三种新的枚举坐标对网格顶点进行编码。初始控制网格按扇区分割后,其顶点被编码到一张纹理上,控制顶点的不规则性分离到扇区的同时扇区之间又具有松耦合联系,使GPU像素管线的并行性从片段网格内扩展到整个网格。另外,通过三张查找表来降低实时计算量并且避免了在CPU上预先细分一次。经过实验对比,本文方法具有更高的实时性能。
关键词:细分曲面、GPU、扇区、枚举系统
Fully GPU Implementation Of Subdivision Surfaces
Zhang Jiahua Liang Cheng Li Guiqing
(College of Computer Science and Engineering, South China University Of Technology , Guangzhou Guangdong, 510640, China)
Abstract A novel strategy is proposed for fully GPU Implementation of subdivision surfaces, using multi-pass general-purpose computation on GPU to accomplish refinement. “fully implement” includes two meanings: The first one is highly using the capability of GPU, The second one is fully processing on GPU. Sector based idea is introduced and three novel enumeration systems are proposed to encode vertices. Vertices in the same depth can be encoded to a texture after partitioning by sectors and the irregularity of control vertices can be partitioned to sector while sectors are low coupling with each other so that concurrent processing can expand from fragment mesh to entire mesh. In addition, three lookup tables are used in order to reduce computing cost and avoid first refinement on CPU. According to experiment, the proposed strategy has better real-time performance and the real-time deformation and editing and be done better.
Key words subdivision surface,GPU,sector,enumeration system
细分曲面已成为图形学最常用的表示技术之一,在一些领域它甚至取代了NURBS。几乎每个大型3D造型与动画设计系统都支持细分曲面造型方法。Pixar的A Bug’s Life(虫虫特工队),Finding Nemo(海底总动员),The Incredibles(超人特工队)都使用了细分曲面造型。Lord of the Rings(指环王)中的Gollum生物就是使用细分曲面造型的。[Bunnell 2005]。
由于细分曲面的顶点和面数以指数速度增长,绘制速度会随细分深度增加而迅速降低,因此采用GPU来加速细分曲面绘制成为一种重要的手段。已有的GPU细分策略需要预先在CPU做一次细分以隔离奇异顶点。在形变和动画过程中,控制顶点每帧都需要改变,在CPU通过半边结构进行一次细分势必会大大降低帧速。为此本文提出一种基于扇区编码顶点元素、通过多趟通用目的绘制在GPU中实现细分曲面的方法,该方法有如下特点:
l 灵活耦合的顶点编码:以扇区为基本单位,组织到一张纹理上。不但扇区内的元素能够相互访问,同一深度所有扇区间的元素都能够相互遍历,使控制顶点的不规则性分离到扇区独立处理的同时仍然具有较好的邻接访问能力。
l 全程GPU细分:使用了三张查找表,无需在CPU做一次预细分,所有细分操作均在GPU中实现,从而支持对控制网格的GPU编辑。
l 高实时性能:同一深度所有顶点组织到一张纹理上,使像素管线的并行性从片段网格内扩展到整个细分网格,每个深度的细分仅调用两次绘制函数,大大减少了纹理和绘制对象上下文的切换,更好地利用GPU大批量处理能力,对于约1000个控制顶点的控制网格细分四次后能够达到100FPS以上。
在GPU上完全进行细分可给动画设计师提供更多的交互自由,能够直接在每帧通过拖曳控制顶点实现定制形变和动画。另外,虽然本文的方法以Catmull-Clark细分曲面为主进行阐述,但容易推广到三角网格上。
后续内容组织如下:第1节介绍相关工作及存在的主要问题;第2节描述所提出的细分框架;第3节简要描述三种基于扇区概念的枚举系统;第4节讨论一次GPU细分的具体细节,第5节给出本文方法的结果以及一些实例。
1.相关工作
细分曲面由拓扑规则和几何规则两类规则构成。前者负责插入新顶点和面得到更细密的网格,后者负责计算新旧顶点的位置使得曲面更光滑。CPU细分可以利用类似半边结构的方式来访问邻接信息。由于此类数据结构不再适用,如何编码邻接信息便成为GPU细分的关键。
考虑到控制网格每个多边形面对应一块细分曲面片,大多数GPU细分方法都是以面为单位进行处理。Bolz等人独立地绘制每个细分曲面片[Bolz 2004],对Catmull-Clark曲面而言,需要以该面片周围一圈四边形面构成的子网作为输入。由于利用预计算的基函数查找表[Bolz and Schröder 2002],进行GPU细分之前需要预先在GPU做一次细分保证每个片最多只包含一个奇异点。该奇异点处的多余顶点需要在专门存储。Brickhill描述了Loop模式的类似实现[Brickhill 2001]。
Shiue等以顶点1-邻域曲面片为绘制单元[Shiue et al. 2005]。其控制顶点为2-邻域子网,称为片断网格(Fragment meshes)。通过螺旋枚举可以把片断网格的所有顶点映射为一行纹理。在Pixel Shader,以特殊的“纹理放大滤波”形式进行细分。计算下一细分层顶点所需要的细分模板以查找表形式保存。由于不同价的查找表不一样,对不同片段网格细分时会导致过多的绘制对象上下文的切换,并行处理只局限在片段网格内部的顶点,价不同的片段网格不能有效地并行绘制,没有充分发挥多象素管线的GPU的并行处理能力。
2. 基于扇区的细分框架
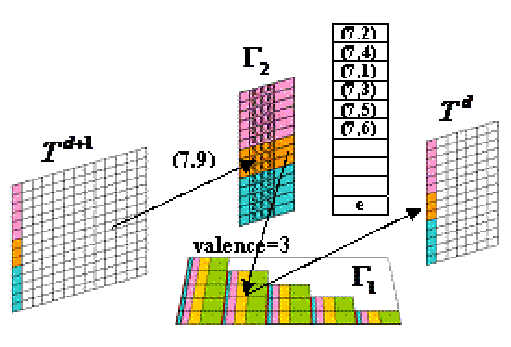
为避免片断网格带来的上下文切换,以更小的区域——扇区作为基本GPU绘制单元。扇区顶点线性地存储在一行纹理上;同一顶点的扇区按逆时针顺序占用连续的纹理行;最后,所有扇区构成一张矩形纹理。最初的扇区为一个四边形。如图1所示,价分别为6, 3, 5的控制顶点共产生6+3+5=14个扇区。初始时,每个控制顶点与它的一个相邻面构成一个扇区, 该控制顶点称为扇区的基点。基点在它的所有扇区上都出现,两个相邻扇区间边界上的其它顶点则列入后一个扇区进行枚举(见3.1节)。
与传统基于面的方法不同,每个扇区只负责绘制相应控制网格四边形面对应曲面片的1/4区域(见图1中的灰色区域),把所有扇区对应的曲面片都绘制后,就得到完整的细分曲面。
记M=<V,F>为原始控制网格,![]() 为控制顶点集。vi的价记为ni,则整个控制网格总的价N如下:
为控制顶点集。vi的价记为ni,则整个控制网格总的价N如下:
最初的时候由CPU把M的N个扇区顶点按前面所述的线性化方法上载到GPU的纹理空间(见图1第2列), 记相应的N×3纹理区域为![]() 。对控制网格的细分变成对扇区的细分。每次细分之后,纹理区域行数保持不变,而宽度增加。d-1次细分后对应的顶点纹理是一个N×(1+Ld+(Ld)2)的矩形区域,记为
。对控制网格的细分变成对扇区的细分。每次细分之后,纹理区域行数保持不变,而宽度增加。d-1次细分后对应的顶点纹理是一个N×(1+Ld+(Ld)2)的矩形区域,记为![]() ,其中Ld为扇区中面的层数,满足:
,其中Ld为扇区中面的层数,满足:
顶点纹理![]() 中每个纹素的RGB代表对应顶点的xyz位置坐标,纹理坐标为顶点枚举编码的索引。与vi
中每个纹素的RGB代表对应顶点的xyz位置坐标,纹理坐标为顶点枚举编码的索引。与vi![]() V第x个面对应的扇区d-1次细分后的结果记为
V第x个面对应的扇区d-1次细分后的结果记为![]() 。第一次细分,即对
。第一次细分,即对![]() 的扇区进行细分时会得到两层顶点和面的新扇区;之后对
的扇区进行细分时会得到两层顶点和面的新扇区;之后对![]() 的扇区时,每次把扇区最外层顶点丢弃(此时,外层顶点不再影响相应曲面片的计算)。
的扇区时,每次把扇区最外层顶点丢弃(此时,外层顶点不再影响相应曲面片的计算)。
GPU中的一次细分通过绘制到纹理实现(Render to Texture,RTT)。进行第d次细分时,Td是源纹理,Td+1是绘制对象。视口初始化为包含N×(1+Ld+(Ld)2)的矩形区域。在Pixel Shader,GPU为每个纹素并行地从上一深度纹理计算获得有影响权重的顶点,再根据模板计算出当前纹素对应顶点的值,输出并渲染为新纹素。
细分到达指定深度后,如果是Shader Model 3.0之前的版本,还需要把以纹理形式存放的顶点转换回顶点缓冲最终绘制顶点到帧缓冲。对于支持Shader Model 3.0的GPU,可以在Vertex Shader中通过Vertex Texture Fetch技术利用tex2DLOD指令直接从纹理纹素得到顶点位置,变换后输出到Pixel Shader,最终绘制到帧缓冲。
每次细分都分成两部分,即不规则顶点计算和规则顶点计算(见第4节)。
图1:流程和数据描述
3. 图元枚举与映射
为了第4节更好地介绍查找表细分的实现细节,本节先介绍三种图元枚举系统,即索引枚举系统(Index Enumeration System, IES);扇区-索引枚举系统(Sector-Index Enumeration System, SIES);扇区-层-索引枚举系统(Sector-Layer-Index Enumeration System, SLIES) 来解决不同环境下的顶点枚举问题,每个系统有两套坐标分别表示整个网格内的全局编码和当前基点扇区内的局部编码。各种枚举系统间转换推导详见[Li et al. 2008]。
3.1 扇区-索引枚举系统(SIES)
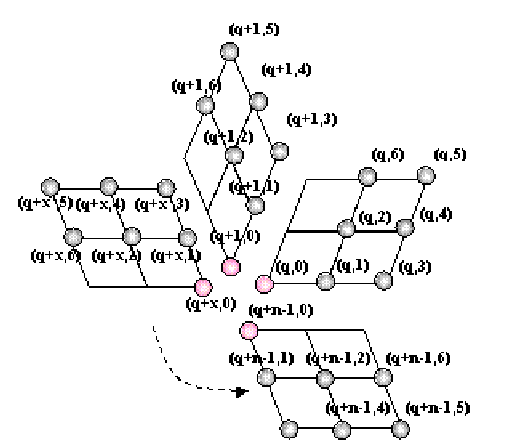
SIES顶点枚举与第2节GPU细分时的顶点存储方式相对应,用于索引纹理Td中的顶点信息。SIES枚举系统用整数对(a,b)来索引顶点,其中a表示顶点在纹理Td中的行号,b则表示该顶点在第a行中的(即相应扇区中的)序号,若以当前基点的扇区为范围进行局部编码,也可以用整数对(a‘,b)来进行索引,其中a‘为以vi为基点的所有扇区中的某个扇区号。如图2所示,每个扇区以基点为中心依次从内到外枚举各顶点,同一层的顶点按逆时针方向枚举。容易知道扇区![]() 中某个顶点的行坐标a存在以下关系:
中某个顶点的行坐标a存在以下关系:
其中qi为从v1到vi-1的基点的价之和,也就是基点的起始扇区号,根据第二节可知a‘与x等价。
图2:邻域顶点的SIES枚举(基点价为n,起始扇区为q)
3.2 扇区-层次-索引枚举系统(SLIES)
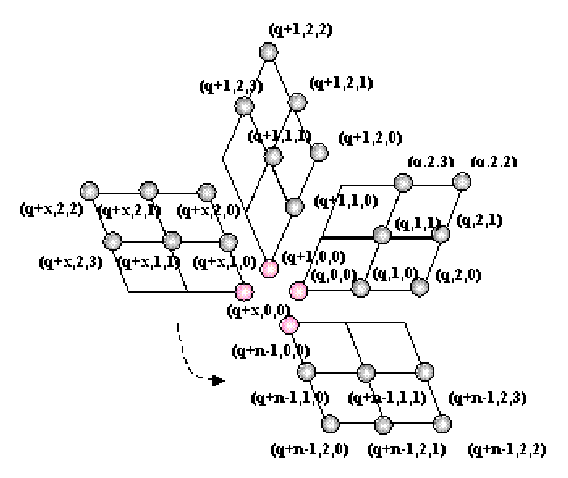
SIES枚举方式能够把扇区顶点映射为一维纹理,但不便于查找元素间的邻接关系。SLIES枚举系统即用于解决这个问题,它由扇区号、层号和层内序号构成,是一种三维坐标系统。因此SLIES坐标(r,s,t)即表示整个网格M中第r个扇区、第s层中的第t个顶点,类似地若在基点的扇区内进行局部编码,可以用三元组(r’,s,t)来进行索引。图3为某个价为nj的基点vj的SLIES坐标编码情况,虽然利用SLIES可以很方便地查找顶点的邻接关系,但网格顶点却是按SIES坐标存放的,因此我们需要从SLIES到SIES的转换公式:
全局SLIES坐标(r,s,t)与局部SLIES 坐标(r’,s,t)满足:
图3:价为n,起始扇区为q的基点2-邻域顶点的SLIES枚举
3.3 索引枚举系统(IES)
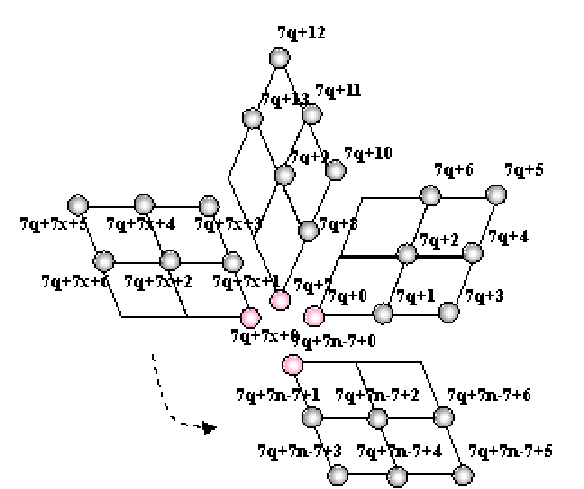
在二维查找表中由于纵坐标需要排列多个模板项,只剩下横坐标排列顶点元素,因此需要一维的枚举系统。IES枚举按行从上到下,行内从左到右对![]() 中的所有顶点线进行线性化,因此价为n的基点会出现n次。图4所给出了
中的所有顶点线进行线性化,因此价为n的基点会出现n次。图4所给出了![]() 的某个基点扇区顶点的枚举情况。
的某个基点扇区顶点的枚举情况。
图4:价为n,起始扇区为q的基点2-邻域顶点的IES枚举
全局IES坐标(ζ)表示整个网格M中按扇区为先序枚举的一维索引,从图4还容易得到在基点vj范围内所有扇区中的局部一维IES索引(ζ‘)。公式(6)实现了从SIES坐标到IES坐标的转换:
全局IES坐标与局部IES坐标存在转换:
3.4 SIES与纹理坐标转换
由于纹理的坐标范围取值从0-1,其二元组(u,v)为横坐标优先,因此全局SIES坐标(a,b)与纹理坐标(u,v)之间仍需要进行如下转换:
其中加上0.5是为了使纹理坐标落在纹素的中心位置,顶点纹理Td宽度为1+Ld+(Ld)2,高为N。
4. 基于查找表的细分
为了计算d次细分后的顶点纹理Td+1上纹素(ad+1,bd+1)的值,需要Td中找到Catmull-Clark模板所需的各个顶点纹素索引集合![]() (注:集合元素设为9的原因见4.2节)。本文也是通过在CPU上预先构建查找表来进行顶点索引,但一次计算整张Td+1纹理,把所有价的模板查找表组合到一张模板查找表Г1一次上传到GPU。如图5所示,图中Г1是模板查找表,它把所有用到的细分权值按价依次存放在纹理空间。为找到(ad+1,bd+1)在查找表Г1中对应的权值信息,需要建立另一张基点信息查找表Г2 记录对应的基点的价(ni)和基点的起始扇区号(qi),以便进行全局坐标与局部坐标之间的转换。
(注:集合元素设为9的原因见4.2节)。本文也是通过在CPU上预先构建查找表来进行顶点索引,但一次计算整张Td+1纹理,把所有价的模板查找表组合到一张模板查找表Г1一次上传到GPU。如图5所示,图中Г1是模板查找表,它把所有用到的细分权值按价依次存放在纹理空间。为找到(ad+1,bd+1)在查找表Г1中对应的权值信息,需要建立另一张基点信息查找表Г2 记录对应的基点的价(ni)和基点的起始扇区号(qi),以便进行全局坐标与局部坐标之间的转换。
根据Td+1上纹素的全局SIES坐标(ad+1,bd+1)查找上一深度顶点纹理Td中有权重贡献的9个顶点的索引过程如下:
1) 根据顶点的行号ad+1在查找表Г2的ad+1行得到对应的基点的价(ni)和基点的起始扇区号(qi)
2) 根据公式(3)把全局SIES坐标(ad+1,bd+1)转换为局部SIES坐标((a’)d+1,bd+1)
3) 根据公式(6)对SIES坐标线性化得到一维的局部IES坐标((ζ‘)d+1)
4) 以(ni×10+j,(ζ‘)d+1)到Г1找出Catmull-Clark模板所需的j从0到8的9个顶点的局部SLIES坐标![]()
5) 根据公式(4)把局部SLIES坐标((r‘)dj,s dj,t dj)转换为局部SIES坐标((a’)dj,bdj)
6) 根据公式(3)把每一个局部SIES坐标((a’)dj,bdj)转换为全局SIES坐标(adj,bdj)
如图5,设查找表最大深度为dmax,dmax=6时根据公式(2)有面层数:Lmaxd=17,![]() =307,需要处理
=307,需要处理![]() 中全局SIES坐标
中全局SIES坐标![]() =(7,9)顶点元素,首先到查找表Г2的第7行找出对应的价为ni =3,基点的起始行号qi=6,同时把全局SIES坐标(7,9)根据公式(3)转换为局部SIES坐标((a’)d+1,bd+1)=(1,9),根据公式(6)线性化后为局部IES坐标(ζ‘)d+1=1×307+9=316,接着以(3×10+j,316)到查找表Г1找出Catmull-Clark模板所需的9个顶点的局部SLIES坐标((r’)dj,sdj,tdj),例如((r’)d0,sd0,td0)=(1,2,2),把局部SLIES坐标(1,2,2)转换为局部SIES坐标((a’)d0,bd0)=(1,5),根据公式(3)把每局部SIES坐标(1,5)转换为全局SIES坐标 (ad0,bd0)=(7,5),接着根据SIES坐标读取Td中具体顶点位置值。
=(7,9)顶点元素,首先到查找表Г2的第7行找出对应的价为ni =3,基点的起始行号qi=6,同时把全局SIES坐标(7,9)根据公式(3)转换为局部SIES坐标((a’)d+1,bd+1)=(1,9),根据公式(6)线性化后为局部IES坐标(ζ‘)d+1=1×307+9=316,接着以(3×10+j,316)到查找表Г1找出Catmull-Clark模板所需的9个顶点的局部SLIES坐标((r’)dj,sdj,tdj),例如((r’)d0,sd0,td0)=(1,2,2),把局部SLIES坐标(1,2,2)转换为局部SIES坐标((a’)d0,bd0)=(1,5),根据公式(3)把每局部SIES坐标(1,5)转换为全局SIES坐标 (ad0,bd0)=(7,5),接着根据SIES坐标读取Td中具体顶点位置值。
图5:查找表细分示意
从T1到T2的细分,由于最外层顶点亦须保存,其计算与后续深度的细分是不同的,需要采用专门的Pixel Shader,其中为找到最外层顶点的计算模板,特别建立了查找表![]() 。算法1是GPU细分基于Direct3D的technique,其中第一次细分用LUTQuadSubdivisionDepth1,之后的细分采用LUTQuadSubdivision。下面分3节分别讨论第一次细分和之后细分的基点以及规则顶点的计算。
。算法1是GPU细分基于Direct3D的technique,其中第一次细分用LUTQuadSubdivisionDepth1,之后的细分采用LUTQuadSubdivision。下面分3节分别讨论第一次细分和之后细分的基点以及规则顶点的计算。
算法1 基于查找表细分的technique
technique LUTQuadSubdivision
{
pass 1: VS IrregularVertex LUTRefinementMain();
PS IrregularVertex LUTRefinementMain();
pass 2: VS RegularVertex LUTRefinementMain();
PS RegularVertex LUTRefinementMain();
}
technique LUTQuadSubdivisionDepth1
{
pass 1: VS IrregularVertex LUTRefinementMain();
PS IrregularVertex LUTRefinementMain();
pass 2: VS RegularVertex LUTRefinementMain();
PS RegularVertex LUTDepth1Main();
}
4.1 各次细分的基点计算
对所有细分深度,基点的计算都是一样的,通过1-邻域顶点以Catmull-Clark细分权值线性组合得到。对于输入的顶点纹理Td+1中的纹素坐标![]() ,首先转换为SIES坐标(ad+1,bd+1),接着通过查找表Г2得到基点的价(ni)和基点的起始扇区号(qi),那么上一深度有权重贡献的顶点索引集合为:
,首先转换为SIES坐标(ad+1,bd+1),接着通过查找表Г2得到基点的价(ni)和基点的起始扇区号(qi),那么上一深度有权重贡献的顶点索引集合为:
.(qi+j,1)对应基点的边邻接点,(qi+j,2)对应基点邻接面对角点(注:起始列号为0)。算法2描述了不规则顶点细分的Pixel Shader,其中MaxValence为基点的最大价,对于GPU Shader来说是一常数,这里取MaxValence=24,βn=3/(2n),γn=3/(4n),αn=1-βn-γn 。
算法2 不规则顶点细分的Pixel Shader
PS_IrregularVertexRefinement(u d+1,v d+1)
{
(a d+1,b d+1)=VertexUVToSIES(u d+1,v d+1);
(i,q,n)=tex2D(Г2,0.5,v d+1);
for(j=0;j<MaxValence && j<n; j++)
{
(u dj,vdj)=VertexSIESToUV(q+j,1);
pdj=tex2D(Td, udj,vdj);
(sj,tj)=VertexSIESToUV(q+j,2);;
rdj=tex2D(Td, sdj,tdj);
}
}
4.2第二次细分及以后的规则顶点的计算
第二次及之后的细分的规则顶点的计算,都需要通过查找表Г1得到模板索引。查找表Г1由多个价的查找表在纵向拼合而成,存放在同一张纹理,以避免纹理上下文切换。记价ni的查找表为Ωn。Ωn的长度为扇区数乘上每个扇区最大细分深度的顶点个数:![]() 。所有Ωn的高度是一样的,还需要一行存储顶点的类型,Catmull-Clark模式的查找表Г1 宽度为10 (9个模版数据项+1个顶点类型项),Loop模式为8。查找表Г1由Ω1,Ω2,...,ΩMaxValence个子表纵向拼接而成,其中MaxValence为所允许的控制网格的最大价,因此Г1就是一个10×MaxValence行,
。所有Ωn的高度是一样的,还需要一行存储顶点的类型,Catmull-Clark模式的查找表Г1 宽度为10 (9个模版数据项+1个顶点类型项),Loop模式为8。查找表Г1由Ω1,Ω2,...,ΩMaxValence个子表纵向拼接而成,其中MaxValence为所允许的控制网格的最大价,因此Г1就是一个10×MaxValence行,![]() 列的矩形纹理区域。
列的矩形纹理区域。
查找表Г1横坐标按局部IES坐标(ζ‘)根据扇区内的顶点编码,编完一个扇区内的顶点再编码下一个扇区的顶点,纵坐标根据价从小到大排列。查找表Г1的每一项是一个四元组:
其中(ζ’)是顶点的局部IES坐标,((r‘)dj,s dj,t dj)是局部SLIES三维坐标,j为模板项的序号。查找表的第(ζ‘)d+1列给出了Md能贡献于Md+1按IES编码的顶点索引集合。第十行存储该顶点的类型(V点、E点还是F点),因此可得公式(9),通过Г1计算Md+1的顶点((a’)d+1,bd+1)的位置:
其中![]() 为访问查找表Г1的函数,f((ζ’)d+1,j) =((r’)dj,sdj,tdj)。处理过程中,首先根据公式(3)通过查找表Г2把全局SIES坐标(
为访问查找表Г1的函数,f((ζ’)d+1,j) =((r’)dj,sdj,tdj)。处理过程中,首先根据公式(3)通过查找表Г2把全局SIES坐标(![]() )转换为局部SIES坐标((a’)d+1,bd+1),对局部SIES坐标((a’)d+1,bd+1)通过公式(6)线性化得到局部IES坐标((ζ’)d+1),通过查找表Г1找到Catmull-Clark模板所需的顶点纹理
)转换为局部SIES坐标((a’)d+1,bd+1),对局部SIES坐标((a’)d+1,bd+1)通过公式(6)线性化得到局部IES坐标((ζ’)d+1),通过查找表Г1找到Catmull-Clark模板所需的顶点纹理![]() 各个纹素的局部SLIES坐标((r’)dj,sdj,tdj),根据公式(4)把局部SLIES坐标((r’)dj,sdj,tdj)转换为局部SIES坐标((a’)dj,bdj),再根据公式(3)通过查找表Г2把局部SIES坐标((a’)dj,bdj)转换为全局SIES坐标(adj,bdj),最后再根据公式(8)转换为纹素坐标(ud,vd),读取顶点纹理Td该纹素得到顶点位置,根据模板加权得到细分后的顶点位置。
各个纹素的局部SLIES坐标((r’)dj,sdj,tdj),根据公式(4)把局部SLIES坐标((r’)dj,sdj,tdj)转换为局部SIES坐标((a’)dj,bdj),再根据公式(3)通过查找表Г2把局部SIES坐标((a’)dj,bdj)转换为全局SIES坐标(adj,bdj),最后再根据公式(8)转换为纹素坐标(ud,vd),读取顶点纹理Td该纹素得到顶点位置,根据模板加权得到细分后的顶点位置。
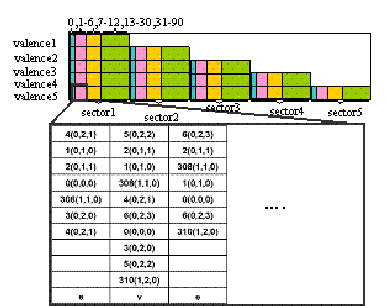
(a) Shuie2005等工作空间螺旋枚举的查找表
(b) 根据SLIES和IES以扇区为先序的查找表
图6:最大价为5的细分曲面查找表Г1
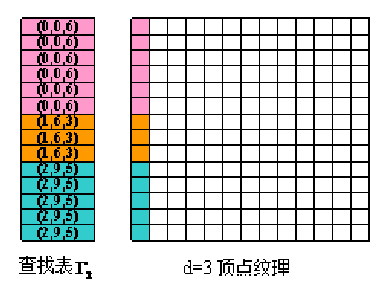
查找表Г2只有一列,高度为N。Г2的每项是一个三元组,它的第k行的元素为(ik,qk,nk),其含义是顶点纹理Td的第l行元素对应着第ik个基点,这个基点的价为nk、第一个扇区的起始行号为qk,因此容易看出同一个基点的三元组元素是一样的,对应于同一个基点vi的元素Г2 (ik,qk,nk)=(i,qi,ni)。图7给出的示例中,Г2的信息说明,前三个基点的价分别为6,3,5,相应地起始行号分别为0,6和9。
图7:左为基点信息查找表Г2,右为顶点纹理顶点纹理T3
算法3 规则顶点第2以上深度细分的Pixel Shader
PS_RegularVertexLUTRefinement_Main (ud+1,vd+1)
{
(a d+1,b d+1)=VertexUVToSIES(u d+1,v d+1);
(i,q,n)=tex2D(Г2,0.5,v d+1);
(ζ d+1)=VertexSIESToIES(a d+1,b d+1);
((ζ’) d+1)=VertexIESGlobalToLocal(ζ d+1,q);
VType=tex2D(Г1,, (ζ’) d+1, n*10+9);
for(j=0;j<9;j++)
{
((r‘)dj,s dj,t dj)=tex2D(Г1,, (ζ’) d+1, n*10+j);
((a’)dj,bdj)=VertexSLIESToSIES((r‘)dj,s dj,t dj);
(adj,bdj)=VertexSIESLocalToGlobal((a’)dj,bdj,q);
(udj,vdj)=VertexSIESToUV(adj,bdj);
Pj=tex2D(Td,, udj,vdj);
}
(VType==1)+pv(VType==2)
}
算法3描述了细分过程的Pixel Shader。 算法首先把输入的Td+1的顶点纹素的纹理坐标(ud+1,vd+1)转换为全局SIES坐标(ad+1,bd+1),再转换为局部SIES坐标((a’)d+1,bd+1),再转换为局部IES坐标(ζ‘)。然后到Г1查找出该顶点的顶点类型VType,再依次从Г1读取9个模板数据项对应的顶点局部SLIES坐标((r’)dj,sdj,tdj),转换为局部SIES坐标((a’)dj,bdj),转换为全局SIES坐标(adj,bdj),再转换为纹理坐标(udj,vdj),通过纹理坐标(udj,vdj)到顶点纹理Td读出顶点位置Pj,根据顶点类型VType选择其中一种模板计算并返回结果。
4.3第一次细分的规则顶点计算
第一次细分,即纹理T2的计算。考虑价为ni的基点vi,设它第一个扇区的起始行号为qi。则vi的新位置也是由它原来的位置与qi到qi+ni-1行的1,2列元素的线性组合得到,因此基点可以按照4.1节计算。接下来考察扇区内基点以外的其他规则顶点元素,规则顶点的新位置也是由它所在的基点的所有邻接点作加权平均得到的。因为第一次细分(d=2)后最外层顶点仍须保留,并参与第2次细分,需要找出相应模板进行正确计算。因此第一次细分还需要一张专门的查找表Г3。查找表Г3的大小和第2深度的顶点纹理![]() 一样大,对于
一样大,对于![]() 中的每个纹素都可以在Г3找到对应的纹素。
中的每个纹素都可以在Г3找到对应的纹素。
图8:第1次细分通过查找表Г3对不规则V点进行拷贝。从左到右依次为原始控制网格,第2深度的细分网格,第2深度细分网格对应的顶点的纹理。
第一次细分时首先按4.1节计算T2中第一列各个扇区基点的值,接着对扇区中其余规则顶点,根据顶点类型分别处理:F点仍然通过读取查找表![]() 得到上一深度有贡献模板权重的各个顶点;E点根据原始控制网格的拓扑关系访问片段网格外部扇区的顶点;V点,第1深度每个扇区外围一圈顶点都对应其他扇区的不规则V点,因此第2深度V点的值只要通过查找表Г3找回第一列中已经计算好的不规则V点就可以了。因此Catmull-Clark模式第一次细分的计算如下:
得到上一深度有贡献模板权重的各个顶点;E点根据原始控制网格的拓扑关系访问片段网格外部扇区的顶点;V点,第1深度每个扇区外围一圈顶点都对应其他扇区的不规则V点,因此第2深度V点的值只要通过查找表Г3找回第一列中已经计算好的不规则V点就可以了。因此Catmull-Clark模式第一次细分的计算如下:
(8)
对于E点,g为访问查找表Г3的函数,g(aj2, bj2,j) =(aj1, bj1),g函数直接在Г3对应位置找到Catmull-Clark模板E点所需的上一深度顶点纹理T1的6个顶点纹素坐标(aj1, bj1);对于V点,h也是访问查找表Г3的函数,![]() ,如上所述
,如上所述![]() 为第一列中已经计算好的不规则V点的值,接着拷贝到顶点纹理T2中的(a2,b2)纹素。如图8,对于T2中第5行第4个纹素,其SIES坐标(4,3),根据原始网格的拓扑关系,在Г3中可以找到它对应橙色片段网格的中心不规则V点,其SIES坐标为(0,6),因此查找表Г3中第5行第4个纹素的值为(0.5/7,6.5/N,0,2)。
为第一列中已经计算好的不规则V点的值,接着拷贝到顶点纹理T2中的(a2,b2)纹素。如图8,对于T2中第5行第4个纹素,其SIES坐标(4,3),根据原始网格的拓扑关系,在Г3中可以找到它对应橙色片段网格的中心不规则V点,其SIES坐标为(0,6),因此查找表Г3中第5行第4个纹素的值为(0.5/7,6.5/N,0,2)。
5. 实验与讨论
三个查找表已离线生成,因此CPU阶段只须读入查找表及控制网格信息,并把控制网格分割为一个个扇区,其计算复杂度为O(N)。在GPU阶段, Vertex Shader对于每个深度细分只分别变换不规则顶点纹理的矩形区域和规则顶点纹理的矩形区域,共处理8个顶点。分裂后的各个深度网格Md整体排布到一张顶点纹理Td,每个深度的绘制函数仅调用两次,绘制对象上下文的切换不再成为瓶颈。通过NVIDIA PerfHUD 5.0进行观察以及上文的分析可知,计算量主要取决于Pixel Shader逐纹素计算新的顶点纹理,以及查找表纹理的随机访问消耗。
图9:细分效果,从左到右从上到下依次对应Frog,Rockarm,Kelin,Ax,CubeHC五个模型
在一台带有512M显存,24个象素管线的NVIDIA 8800 GTX GPU以1024×768屏幕分辨率进行实验,在CPU上对原始控制网格的顶点数组不断修改实现形变,CPU上顶点数组根据拓扑分裂为一个个扇区映射排布到第1深度的顶点纹理T1上。经过多次细分后,在最终网格绘制时,通过Vertex Texture Fetch读取细分好的纹理上的顶点数据并绘制到帧缓冲。对于中等大小1000控制顶点左右的模型有24以上FPS值表现,能够满足视觉要求。目前主流的GPU对于绘制对象型纹理一般支持到4096×4096大小,而顶点纹理Td的大小为W×N,因此N应该小于4096,根据表2,深度d最大为7。图9依次给出表1各个网格在深度4下绘制的效果。
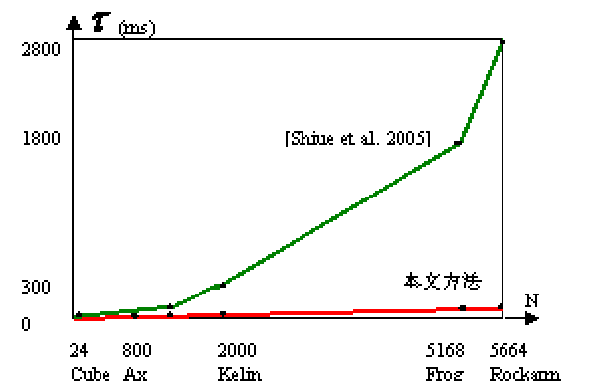
与[Shiue et al. 2005]工作进行对比,从表1可以看到,FPS值有了大幅提高。图10对两种方法的处理时间进行了对比。
表1:各个模型细分数据,表中FPS值表示为r1/r2,r1为本文方法的FPS值,右侧为[Shiue et al. 2005]方法的FPS值,?表示无法得到实验结果:
| 模型名 |
N |
深度 |
||||
| 1 |
2 |
3 |
4 |
5 |
||
| Rockarm |
5664 |
922/40 |
461/14 |
329/4 |
179/1 |
76/? |
| Frog |
5168 |
994/41 |
792/14 |
428/4 |
208/1 |
82/? |
| Kelin |
2000 |
1020/144 |
879/55 |
779/13 |
447/4 |
197/1 |
| CubeHC |
1280 |
1018/189 |
889/166 |
837/46 |
580/19 |
284/13 |
| Ax |
800 |
1024/301 |
893/250 |
842/134 |
765/30 |
405/17 |
图10中纵坐标为每帧处理时间τ=1/FPS-μ,μ为每帧用于其他操作的时间,本实验为0.88ms。本文方法(图10中红色曲线)每帧处理时间τ与N基本成线性关系,这与用于细分的绘制函数仅调用2×细分次数相符;而[Shiue et al. 2005] (图10中绿色曲线)按相同的价进行分组细分后,τ仍随N的增长而急剧增加,这是由于片段网格即使按价分组后,作为绘制对象仍需要逐一切换绘制对象上下文,其绘制函数的调用次数为片段网格数N×细分次数。
图10:同一深度(d=4)下N与τ的关系
已知每个深度一个扇区的顶点数为W=(1+Ld+(Ld)2),又有![]() ,用ψ(d)表示从1到d深度一个扇区顶点数之和,则有:
,用ψ(d)表示从1到d深度一个扇区顶点数之和,则有:
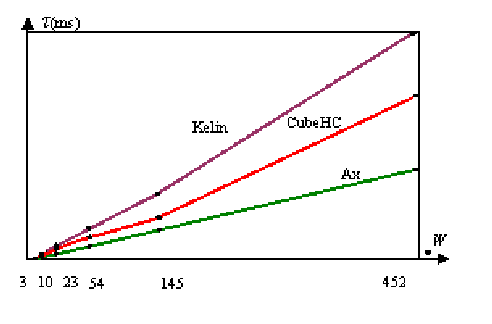
那么细分到d深度Pixel Shader共要处理ψ×N个纹素。表2给出了同一个模型不同细分深度下ψ与τ关系。从图11可以看出随着细分深度的增加,每帧时间τ并不线性于扇区内顶点数量,而是近似线性于累计扇区顶点数量ψ。因为每多细分一个深度需要累加上一深度的细分计算量,所以大批量处理(Large Batch)带来的增益很明显。
表2:同一模型不同细分深度下ψ与τ关系
| d |
L |
ψ |
τ(ms) |
|||
| Kelin |
Ax |
CubeHC |
||||
| 1 |
1=0+1 |
3 |
3 |
0.10 |
0.10 |
0.10 |
| 2 |
2=1+1 |
7 |
10 |
0.25 |
0.24 |
0.24 |
| 3 |
3+2+1 |
13 |
23 |
0.40 |
0.31 |
0.31 |
| 4 |
5=4+1 |
31 |
54 |
1.35 |
0.44 |
0.84 |
| 5 |
9=8+1 |
91 |
145 |
4.20 |
1.59 |
2.64 |
| 6 |
17=16+1 |
307 |
452 |
14.99 |
5.79 |
10.61 |
图11:同一模型不同细分深度下ψ与τ关系
本文方法在GPU上实现所有深度的细分,动画设计者简单地在屏幕上拾取若干控制顶点,通过拖曳这些控制顶点编辑以产生动画或形变过程,比需要在CPU完成一次细分的方法有更快的响应时间。图12给出了形变的效果。
图12:Catmull-Clark细分曲面实时形变(Rockarm模型)
6 小结与展望
通过把网格分割为更小的扇区单元进行处理,使得不规则性独立分离到扇区,之后再整体组织到一张顶点纹理上能够更好地获取邻接关系,对于扇区中的任意一个元素都能获取任意片段网格中的扇区的元素,能够在GPU中更好地并行处理。对方法中的查找表在自动生成时作简单修改就能支持三角形网格的Loop模式细分。在未来,将考虑如何在GPU上实现尖锐特征以及细节保持,以及添加位移贴图实现几何细节。鉴于已经能够在GPU完全实现细分,可以给控制顶点分别设置轨迹路径实现更为复杂的动画和形变过程。
致谢
本文的工作受国家自然基金(60673005)和广东省自然基金(05006540)支持。
参考文献
1. BRICKHILL, D. Practical Implementation Techniques for Multi-Resolution Subdivision Surfaces. In Game Developers Conference. 2001.
2. BOLZ J., AND SCHRöDER P.: Evaluation of subdivision surfaces on programmable graphics hardware. http://www.multires.caltech.edu/pubs/GPUSubD.pdf.
3. BOLZ J., AND SCHRöDER P.: Rapid evaluation of Catmull- Clark subdivision surfaces. In Proceedings of the Seventh Intertional Conference Web3D Symposium 2002, 11-18.
4. BUNNELL, M. GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation.Addison-Wesley, Reading,MA, ch. Adaptive Tessellation of Subdivision Surfaces with Displacement Mapping. 2005.
5. CATMULL, E., AND CLARK, J. Recursively generated Bspline surfaces on arbitrary topological meshes. Computer Aided Design, 1978. 10, 350–355.
6. LI GUIQING, ZHANG JIAHUA, LIANG CHENG. GPU-based Composite Subdivision. 待发表. 2008
7. LOOP, C. Smooth Subdivision Surfaces Based on Triangles. Master’s thesis,University of Utah, Department of Mathematics. 1987.
8. LOSASSO, F., HOPPE, H., SCHAEFER, S., AND WARREN, J. Smooth geometry images. In Proceedings of the symposium on Geometry processing, 2003.138–145.
9. PETERS, J. Patching Catmull-Clark Meshes. In Proceedings of SIGGRAPH, 2000. 255–258.
10. SHIUE L.-J., JONES I. AND PETERS J.: A realtime GPU subdivision kernel. ACM Transactions on Graphics (Proc. SIGGRAPH 2005), 22(3):1010-1015.