“泰迪杯”挑战赛 - 通过聚类方法对航空客运的客户进行细分

目 录

1. 挖掘目标
2. 分析方法与过程
   2.1. 总体流程
   2.2. 具体步骤
   • 步骤一：数据预处理
   • 步骤二：群体聚类
   • 步骤三：行为特征聚类
   2.3. 结果分析
   • 第一类：
   • 第二类：
   • 第三类：
3. 结论
4. 参考文献

1. 挖掘目标

本次建模目标是在航空公司的海量会员数据中选择符合此研究方向的评价基础属性并分析与各属性之间的相关性，从而发现并选择相关属性集；构建反映客户价值评价指标体系，聚类出行为特征一致的客户，从而可对具有特定行为特征的群体进行相应的营销策略。

2. 分析方法与过程

2.1. 总体流程

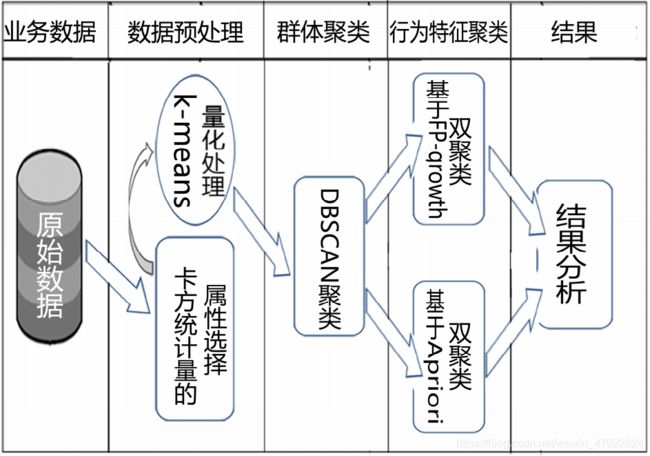
主要包括如下步骤：
步骤一：数据预处理，根据经营策略选择评价属性，对所有属性与评价属性之间进行相关性分析，去除属性集中的弱相关项与冗余项从而达到数据简化的目的。

步骤二：群体聚类，用 K-means 算法将每个属性的原始数据划分为三个级（1,2,3），再由基于密度可达的 DBSCAN 算法进行客户聚类，将所有客户大体上分为高，中，低三个等级。

步骤三：行为特征聚类，用双聚类分别对步骤二的三个等级的聚类结果分别做行为特征聚类，采用基于了基于 apriori 的双聚类和 FP-growth 的双聚类。

步骤四：结果分析，挖掘最终聚类结果中的信息并提出相应的营销策略。

2.2. 具体步骤

• 步骤一：数据预处理 数据预处理

A. 数据简化

数据简化在对挖掘任务和数据本身内容理解的基础上，寻找依赖于挖掘目标的表达数据的有用特征，以缩减数据规模，从而在尽可能保持数据原貌的前提下最大限度地精简数据量。针对数据库中的属性进行属性选择[1].

B. 研究方向与分类属性选择

针对不同的经营策略，评价标准往往是不同的，因而客户细分的结果也不同。本文以航空公司营业额为研究背景，选择总售票价为分类属性[2]（为原始数据中提供第一年和第二年的售票价的和），并基于此分类属性进行属性选择。

C. 数据均匀量化

由于原始数据中每个属性自身的数值差距与属性与属性之间的数值差距都很大，所以对原始数据按量化区间间隔进行均匀量化。即参照某个属性数值的整体跨度将此属性出于某一区间的所有值仅用一个数值代替。通过数据均匀量化，使下面进行属性选择时的时间复杂度与空间复杂度大幅减低，并减少属性间数值差距的影响。

D. 属性选择——基于卡方统计量

本算法利用卡方统计量度量每个属性与分类属性的相关性，按照相关性排列各个属性，并将属性划分为三个等级：强相关、相关、弱相关，去除弱相关属性及冗余重复属性，利用 等级临界值，选择出相互独立的属性[3]。

E. 算法思想

a) 利用列联表计算每个属性 Fi 与分类属性 C(本实验选择总票价作为分类属性)的卡方值Ki,C。

b) 根据 a 结果排列各个属性。

c) 将所有属性聚成三类，即强相关（Strong Relevant）子集、相关（Relevant）子集、弱相关（Weak Relevant）子集。确定最弱强相关（the Weakest of Strong Relevant）属性 FWoS 和最强弱相关（theStrongest of Weak Relevant）属性 FSoW。

d) 对于强相关属性子集 SSR，选择参照属性 Fi，遍历子集中的其它属性 Fj 计算 Ki,j；如果 Ki,j 大于或等于 KWoS,C，删除该属性，否则保留；将 Fi 放入强相关约简（the Reducof Strong Relevant）属性子集 SRSR；如果 SSR 不空，继续 d。

e) 对相关属性子集 SR 中的所有属性 Fi 对强相关约简属性子集 SRSR 中的每个属性 Ki,如果Ki,j 大于 KSoW,C，将 Fi 删除；如果 Fi 未被删除，将 Fi 放到相关约简（the Reduct of Relevant）属性子集 SRR 中；

f) 将弱相关属性子集 SWR 删除。

F. 算法实现

根据上一点的算法思想，这里给出在 matlab 平台上实现本算法的伪代码。为减少建立列联表时占用过多的资源，已将每个属性的原始数据梯度量化。

输入：S（F0,F1，F2…FN）// 梯度量化后的属性子集 
C // 分类属性（总票价属性） 
输出：S’ // 相关属性集 
a) For i=1:N 
T=Table(Fi,C); // 形成属性 Fi 与分类属性 C 的列联表 
Ki=Calculate(T); // 利用列联表计算卡方值Ｋｉ 
b) Sort(S) // 将ａ）得出的 Ki 按顺序排列 
c) Rank(S) // 通过 K-means 算法将 S 聚为三类，得到 SSR(强相关集)，SR（相关集）和 SWR(弱相关集) 
d) F=GetFirst(SSR) 
while(Fp≠ NULL) //去除强相关属性子集中的冗余属性 
{
      
Fq= GetNext(SSR, Fp); //取子集中下一个元素 
while(Fq≠ NULL) 
{
      
tp,q= Table(Fp, Fq); 
Kp,q= Calculate(tp,q); 
Fq′ = Fq; 
if(Kp,q≥WSδo) 
Delete(SSR, Fq); //删除子集中的当前属性 
Fq= GetNext(SSR, Fq′); 
} 
Fp= GetNext(SSR, Fp); 
} 
e) F=GetFirst(SR) 
while(Fp≠ NULL) 
{
      
Fp′ = Fp; 
Fq= GetFirst(SSR); 
while(Fq≠ NULL) 
{
      
tp,q= Table(Fp, Fq); 
Kp,q= Calculate(tp,q);
if(Kp,q>SWδo) 
{
      
Delete(SR, Fp); 
break; 
} 
Fq= GetNext(SSR, Fq); 
} 
Fp= GetNext(SR, Fp′); 
} 
f) S’=Combine(SSR,SR); 
g) Return S’;

G. 运行结果

以原始数据中的第一年总售价和第二年总售价（EXPENSE_SUM_YR_1，EXPENSE_SUM_YR_2）的和——总售价（EXPENSE_SUM）为分类属性，对所有数值型属性进行基于卡方统计量的属性选择。得出相关属性集结果如下：

这个属性集中的属性都与分类属性有很大的相关性，其卡方统计量的值都比较大且已经不 存在冗余属性。同时，此属性集基本能与评价客户价值的 RFM 模型相对应。

• 步骤二：群体聚类

A. DBSCAN 算法：

DBSCANS 算法是一个基于密度的聚类算法[4]。该算法通过不断生长足够高密度区域来进行聚类；它能从含有噪声的空间数据库中发现任意形状的聚类。DBSCAN 方法将一个聚类定义为一组“密度连接”的点集。通过此算法可以将所有客户大体上分为高，中，低三个等级，达到群体聚类的目的。

B. 算法思想：

(1)输入聚类数据,然后任意选取一个数据点 x,检查数据点 x 的 Eps 邻域。

(2)如果 x 是核心点而且没有被划分到某一个类,则找出所有从 x 密度可达的点,最终形成一个包含 x 的类。

(3)如果 x 不是核心点,则被当做噪声处理。

(4)转到第一步,重复执行算法;如果数据集合中所有的点都被处理,则算法结束。

C. K-dist 图：

对输入参数 Eps 敏感是 DBSCAN 算法的主要缺点之一。而 k-dist 是解决这个问题的好方法， K-dist图的思想[5],计算每个数据第K个最近邻居之间的距离,然后对距离聚类,实现数据分区。为了确定 Eps，DBSCAN 需要计算所有数据对象与它的第 k(一般 K 取整个数据集的 1/25)个最邻近的对象之间的距离，并将结果按距离排序，产生 k-dist 图。k-dist 图中的横坐标则为对应于某一 k-dist 距离值的数据对象的个数；纵坐标表示数据对象与它的第 k 个邻近对象间 的距离。然后,按原 DBSCAN 启发式方法寻找 K-dist 排序图的第一个凹陷(阈值点),从而确定Eps 的值[6]。

然而在寻找和绘制 K-dist 图却需要耗费大量的时间和资源。为了更好的实现这个方法，我们采用了 java 的 Fork/Join 框架下的并行计算，将总的任务分解成多个子任务，并且组合多个子任务的结果就能够获得最终的答案，原理如图：

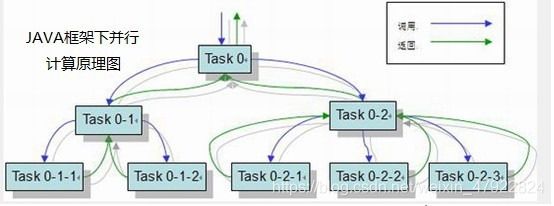
并在 K-dist 按距离排序时，采用了快速排序的方法，减少时间复杂度，加快其运行速度。

D. 原始数据的处理

在原始数据、或者是经过标准差处理的标准化数据，进行 DBSCAN 聚类时，由于原始数据的跨度过大、而标准化的数据分类不明显，导致聚类效果不佳，只能聚成一大类，和一些噪点， 达不到聚类的效果。因而我们进行了数据处理，使用 K-means 将数据聚成 3 类，将客户属性分成 1、2、3 三种，即是低、中、高三种客户属性。

E. K-means 算法:

K-means 算法是一种动态聚类方法[7]，这种方法先选择若干样本作为聚类的中心，在按某种聚类准则（通常采用最小距离原则）使各种样本向各个中心积聚，从而得到初始的分类，然后，判断分类的合理性，如果不合理，就修改分类，如此反复的修改聚类的迭代运算，直到合理为止。

F. 多种算法的伪代码

DBSCAN 算法伪代码 算法伪代码：

输入：数据对象集合 D，半径 Eps，密度阈值 MinPts 
输出：聚类 C 
DBSCAN（D, Eps, MinPts） 
Begin 
init C=0; //初始化簇的个数为 0

for each unvisited point p in D 
mark p as visited; //将 p 标记为已访问 
N = getNeighbours (p, Eps); 
if sizeOf(N) < MinPts then 
mark p as Noise; //如果满足 sizeOf(N) < MinPts，则将 p 标记为噪声 
else 
C = next cluster; //建立新簇 C 
ExpandCluster (p, N, C, Eps, MinPts); 
end if 
end for 
End 
其中 ExpandCluster 算法伪码如下： 
ExpandCluster(p, N, C, Eps, MinPts) 
add p to cluster C; //首先将核心点加入 C 
for each point p’ in N 
mark p' as visited; 
N’ = getNeighbours (p’, Eps); //对 N 邻域内的所有点在进行半径检查 
if sizeOf(N’) >= MinPts then 
N = N+N’; //如果大于 MinPts，就扩展 N 的数目 
end if 
if p’ is not member of any cluster 
add p’ to cluster C; //将 p' 加入簇 C 
end if 
end for 
End ExpandCluster

KDist 伪代码:

输入：数据对象集合 D 
输出：所有数据对象与它的第 k(一般 K 取整个数据集的 1/25)个最邻近的对象之间的距离 
KDist(D) 
Begin 
for each point pi in D//遍历每个数据集里的点 
for i=1：N 
Arraylist[i]=GetKDist(pi) 
end for 
end for 
End
GetKDist（px）//调用 getKDist 
Begin 
inti p=px 
for each point pi in D//遍历每个数据集里的点 
for i=1:N 
if（p != pi）判断是否为同一点 
Arraylist[i] = Getdistance(px,pi)//得到一个点 px 到数据集里其他点距离的集合 
end if 
end for 
end for 
QuickSort(Arraylist[], 0, N-1)//快速排序 
return Arraylist[k-1]返回第 k 近的值 
End 
QuickSort(A，p，r)// 为排序一个完整的数组 A，最初的调用是 QUICKSORT(A，1，length[A]）。 
if p<r 
then q = PARTITION(A，p，r) 
QUICKSORT(A，p，q-1) 
QUICKSORT(A，q+1，r)

快速排序算法：PARTITION

PARTITION(A，p，r) 
x=A[r] 
i=p-1 
forj = p to r-1 
do if A[j]≤x 
then i=i+1 
exchange A[i]←→A[j] 
exchange A[i+1]←→A[r] 
return i+1

K-means 伪代码:

输入：samp（I1，I2，I3…Im）//某个属性的原始数据 
 N //聚成 N 类 
输出：samp1,samp2,…sampN //聚类结果 
th0=1/N*max(samp); th1=2/N*max(samp); …. //初步分类的临界值 
n1=0;n2=0;….nN=0;//各类中元素的个数 
c1=0.0;c2=0.0;….cN=0; 
for i=1:m

samp(i)→samp1 or samp2…//初步划分 
end 
c1=c1/n1;c2=c2/n2;…. //初始每个聚类中心 
t=0; 
cl1=c1;cl2=c2;… 
c11=c1;c22=c2; …//聚类中心 
while t==0 
 for i=1:N 
 samp(i)→min(distance(samp(i),聚类中心))//将元素并入离其最近的那一类中 
 end 
 if c11==c1 && c22==c2 &&…//聚类中心不再变化 
 t=1; 
 end 
 cl1=c11;cl2=c22;… //重新计算聚类中心 
 c1=c11;c2=c22;.. 
end %samp1,samp2 为聚类的结果。

G. 运行结果

①：数据使用 数据使用 kkkk----means means means 处理后的聚类效果 处理后的聚类效果

K-means 算法将数据聚类处理后，用 K-dist 处理画出 K-dist 图(如上)，可以看出凹陷(阈 值点)Eps=1.再由 DBSCAN 算法进行群体聚类。得出如下的 3 类和噪点：

②原始数据的聚类效果 原始数据的聚类效果：

使用原始数据，从上图可以看出阈值点不能有效地为 DBSCAN 确定 Eps 的值，而效果如下：


从上图明显地看出，聚类结果只有一类，它与现实中客户的群体差异化、行为差异化不符；但是，用 K-means 处理后的数据聚类结果中 3 类均值分别为 1、2、2.5 正好把客户分为了低、中、高 3 类，证明了采用 K-means 处理后的数据优于原始数据的聚类。因此选择采用 K-means处理后的聚出的三类客户作为群体聚类结果。

• 步骤三：行为特征聚类

A. 双聚类引入

为了找出某些行为特征相一致的客户，使用双聚类对步骤二中高，中，低三等客户群体同时进行属性和人员的聚类。本论文采用两种双聚类方法：基于 apriori 的双聚类[8]和基于FP-growth 的双聚类[9]。聚类结果即为具有具有相同行为特征的人群[10]。

B. 基于 Apriori 的双聚类

基本流程：
a) 第一次扫描航空数据库 D 时，产生 1-频繁集。

b) 由 1-频繁集两两组合生成 2-频繁项集，同一属性不用组合。

c) 再由 2-频繁项集对比筛选，连接生成 3-频繁集。如此类推，由 k-1 –频繁项集对比筛选，连接生成 k-频繁集。在生成第 k-频繁项集时候，要注意要进行拼接两个的 k-1 – 频繁集里， 其属性和其取值都应该只有一个不同。

d) 如此直到 k 到最大值或已无频繁集可生成。
例如：有两个属性 A 和 B。其值都可取为 1 和 2。对这两属性的矩阵进行双聚类。利用上面的方法，得到每步储存的情况。见下图。其中 A1 代表属性为 A，值为 1 所有记录的一个集合。A1B1 代表属性为 A、B，值分别为 1,1 时所有记录的一个集合。

基于 Apriori Apriori 双聚类的伪代码 双聚类的伪代码

• 输入： 
1) 格式为( id， itemset) 的事务数据库 D，其中 id 为会员的 id，itemset 为该记录所对应的每个属性的等级的集合； 
2) 用户支持度 min_sup。 
• 输出：所有的频繁项目集所对应的子矩阵。 
1) L1=find_frequent_1- itemsets(D);//找出所有的频繁1 项集 
2) for(k=2; Lk- 1≠Φ; k++){
      
3) Ck=apriori_gen( Lk- 1， minsup); 
4) for each transaction t∈D do {
     //扫描 D 以计数 
5) Ct=subset (Ck， t);//取出记录 t 中包含的候选集
6) for each candidate c∈Ct 
7) c.count ++; 
8) } 
9) Lk={
     c∈Ct| c.count≥minsup} 
10) } 
11) return L=∪kLk;//求 Lk 的并

其中， apriori- gen 是以频繁(k- 1)项目序列集 Lk- 1 为自变量的候选集生成函数。 该函数返回包含所有频繁 k 项目集的超集，分链接和修剪两步执行：

第1 步：链接(join)

Procedure apriori_gen(Lk- 1:frequent(k- 1)- itemsets; minsup) 
1) for each itemset l1∈Lk- 1 
2) for each itemset l2∈Lk- 1 
3) if ((l1[1]=l2[1])(l1[2]=l2[2])∧…∧(l1[k- 2]=l2[k- 2])∧(l1[k- 1]≠l2[k- 1])then {
      
4) c=l1∪l2；//连接， 产生候选集 
5) if has_infrequent_subset(c，Lk- 1) then 
6) delete c;//修剪， 去掉无用的候选项 
7) else add c to Ck; 
8) } 
9) return Ck;

第2 步: 修剪(prune)

procedure has_infrequent_subset(c: candidate k- itemset;Lk- 1: frequent(k- 1)- itemsets);//使用先前的知识 
1)for each (k- 1)- subset of 
2) if s∈Lk- 1 then 
3) return true; 
4) return false; 对 Ck 中的任一候选集 c， 如果 c 中存在一个不属于 Lk- 1 的长度为 k- 1 的子序列， 那么就从 Ck 中
删除该候选集 c。

最后把 Ck 中的结果输出对应的子矩阵即为所找的双聚类。

C. 基于 FP-growth 的双聚类

基本思想流程：

a) 第一次扫描航空数据库 D 时，产生 1-频繁集。

b) 由所有的 1-频繁集组合成深度优先的 k-项集。

c) 再把所有的 k-项集作为数据集进行 FP-growth 寻找频繁项集。

d) 输出找到频繁项所对应的子矩阵。

例如：有三个属性 A、B 和 C。其值都可取为 1 和 2。对这三个属性的矩阵进行双聚类。利用上面的方法，得到每步储存的情况。见下图。

其中 A1 代表属性为 A，值为 1 所有记录的一个集合。A1B1 代表属性为 A、B，值分别为 1,1 时所有记录的一个集合。其他以此类推。

最后输出由 fp-growth 找到的频繁项对应的子矩阵。

基于 fp-growth 的双聚类伪代码：

procedure FP_growth(Tree, a) 
if Tree 含单个路径 P then{
      
 for 路径 P 中结点的每个组合（记作 b） 
 产生模式 b U a，其支持度 support = b 中结点的最小支持度； 
} else {
      
 for each a i 在 Tree 的头部(按照支持度由低到高顺序进行扫描){
      
 产生一个模式 b = a i U a，其支持度 support = a i .support； 
 构造 b 的条件模式基，然后构造 b 的条件 FP-树 Treeb； 
 if Treeb 不为空 then 
 调用 FP_growth (Treeb, b)； 
 } 
}

最后输出由 fp-growth 算法找出的频繁项所对应的子矩阵。

2.3. 结果分析

（注释：表格中的 3,2,1 分别代表等级高，中，低。斜下框线表示不考虑此属性）

• 第一类：

第一类双聚类结果：


在对 52946 个客户数据进行双聚类后,可以看出，这人群里面的人的所有行为习惯都处于低档 水平。但是里面唯有一个属性飞行次数达到了中档水平。说明这些人里面的不乏那些乘机次数比较多次的人。这些人属于那种较少参与消费的人群。如何提高航空公司的销售额，就要看航空公司怎样推行自己的服务，刺激人群消费。

• 第二类：

第二类双聚类结果：

这是一个中档客户群体，可以看成是潜在价值的客户,有针对性的营销策略可将其发展为高价值客户，其中各行可以代表不同的行为特点。

① 如上图第二行和第三行

这些客户的积分水平都一般。但是其他各项，如消费，飞行次数、公里都达到了不错的水平。

② 在这些中档客户中，可以看出他们各个属性都是值为 2（即中等价值）时人数最多。 只有一个是例外的。就是ELITE_POINTS_SUM值为1有7865人。因此可以看出在中档客户这个阶 层的人里面。鲜有参与到更高层次的活动（如购买航空公司推销的商品等）。

③ 在这个阶层的客户里面，积分显得不是那么重要，有人积分低但是其对消费额的贡献是 巨大的。
如以下这类群体：

所以，我们不能差异对待这类客户。

• 第三类：

第三类双聚类结果：

1.高档客户的基本积分，飞行次数，公里等都达到了最高等级。但是其精英积分，消费水平，还有总积分在一定程度上还有提升的空间，所以如何想方法刺激这群客户消费是有必要的。

2.高档客户的消费水平本应该是很高的。但在所有 331 个人中有 295 人消费水平集中在值为 2（即中等水平）的范围里[11]。所以十分有必要给予他们更加优惠的政策，刺激他们的消费欲望。

3.作为高档用户，他们中大部分人都的BASE_POINTS_SUM（基本积分）只是中等水平。所以对这部分群体的有关基本积分业务工作应该加强。

3. 结论

总的来说，这次比赛，我们从航空会员数据的特点出发，根据 CRM 和卡方统计量方法对属性进行了选择和约简，得到了多个客户属性中重要的属性集。然后用 DBSACN 把客户分成三类，在这三类里面再用基于 apriori 和基于 FP-growth 的双聚类算法进行实验，实验表明，我们得到的双聚类结果能够精确和细致的对客户行为进行细分。

其中的所有流程，我们都已经自己编程实现了。而且，我们严格按照数据挖掘的流程来进行，进行了大量的工作，所有步骤都有根有据，得出来的结果也都符合客观实际。

比如：我们用卡方统计量来作为数据预处理的时候，得出的属性和已有的传统基于 RFM模型方法聚类所选择的属性大致相等。比如：我们用 DBSCAN 时候为了确定其 eps，做了许多样本去进行 k-dist 试验，最终才得出先把数据 k-means 分成三类，效果最好。又比如：用DBSCAN 算法成功把客户分成三类后，用双聚类的时候证明了这三类结果是符合预期的，即较好地把客户分成高中低三档。而且，我们为了提高效率，特地还用了并行编程；另外，我们实现了基于 Apriori 的双聚类和基于 fp-growth 的双聚类。

4. 参考文献

[1] 邵进智．基于属性间相关性分析的属性选择方法研究[D].北京：北京交通大学，2009．

[2] 曹源．基于属性间相关性分类理论的属性选择方法研究[D].北京：北京交通大学，2008．

[3] 刘辉．数据挖掘中约简技术与属性选择算法的研究[ D].吉林: 吉林大学, 2006．

[4] 王翠茹，朵春红．一种改进的基于密度的DBSCAN聚类算法[J]．广西师范大学学报(自然科学版)，2007（4）：104-107．

[5] 任兴平．何忠龙，孟增辉.改进DBScAN算法中参数EPs值的确定[J].现代电子技术， Vol.Zo(No.ll)，2007:120一121.

[6] 蔡颖琨，谢昆青，马修军．屏蔽了输入参数敏感性的DBSCAN改进算法[J]．北京大学学报(自 然科学版)，2004（3）：480-486．

[7] 吴夙慧，成颖，郑彦宁，等．K-means算法研究综述[J]．现代图书情报技术，2011（5）：28-35．

[8] 秦如新，田英杰，陈静，等． 双聚类的关联规则挖掘方法［J］． 北京工业大学学报， 2009， 35( 4) : 561-565．

[9] 孙自广．FP-growth频繁集挖掘算法的分析与实现[J]．广西工学院学报，2005（3）：64-67．

[10] 张敏，戈文航．双聚类的研究与进展[J]．微型机与应用，2012（4）：4-6,10．