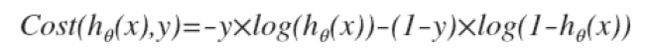用途:分类问题
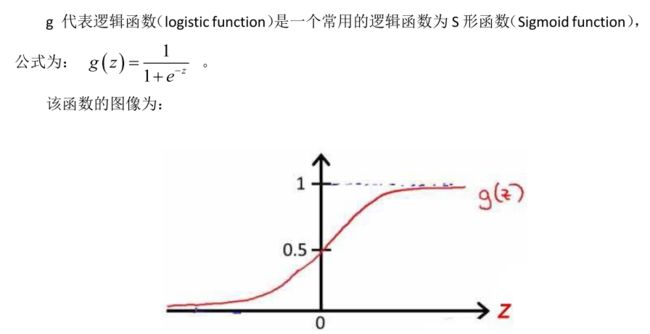
假设函数:
我们就是要通过训练样本来确定theta的取值
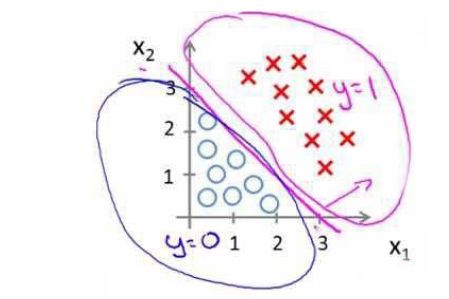
z=Theta^t*x在样本的图像上即是分类的分界曲线,即求得theta就可以判断实验样本的分类
theta^*x表示边界图像
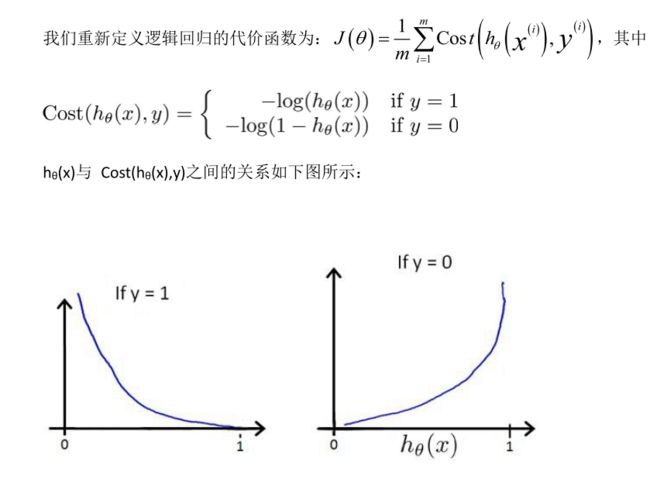
代价函数:
一般来说代价函数为误差的平方和
但对于h(x)误差的平方和为非凸函数所以
将其写成一个式子:
通过梯度下降算法求theta:
代码:
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet():
dataMat=[];labelMat=[]
with open('testSet.txt') as f:
lineArr=f.readlines()
for line in lineArr:
line=line.strip().split()
dataMat.append([1.0,float(line[0]),float(line[1])])
labelMat.append(int(line[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatin,classMatin):
dataMatrix=mat(dataMatin)
labelMatrix=mat(classMatin).transpose()
alpha=0.01
Maxcycletime=500
m,n=shape(dataMatrix)
weight=ones((n,1))
for k in range(Maxcycletime):
h=sigmoid(dataMatrix*weight)
cost=(labelMatrix-h)
weight=weight+alpha*dataMatrix.transpose()*cost
return weight
def plotBestFit(wei):
weight=wei.getA()#将矩阵转化为数组
dataMat,labelMat=loadDataSet()
dataArr=array(dataMat)
n=shape(dataArr)[0]
xcord1=[];ycord1=[];
xcord2=[];ycord2=[];
for i in range(n):
if int(labelMat[i])==1:
xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
ax.scatter(xcord2,ycord2,s=30,c='green')
x=arange(-3.0,3.0,0.1)
y=(-weight[0]-weight[1]*x)/weight[2]
ax.plot(x,y)
plt.xlabel('X1');plt.ylabel('X2');
plt.show()
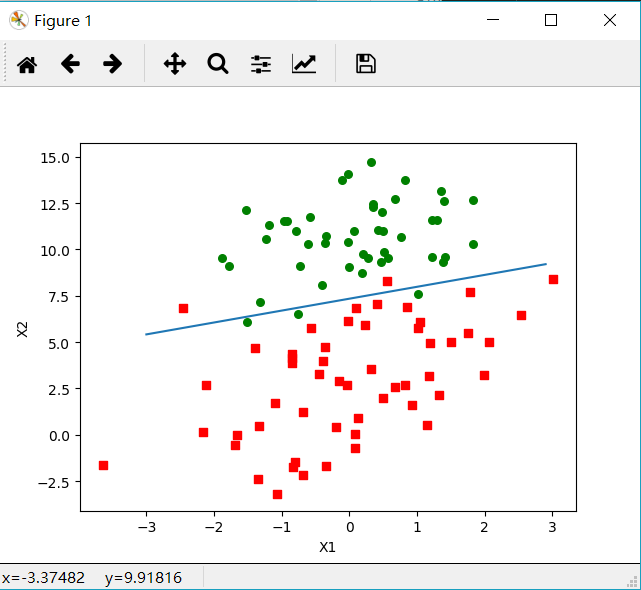
运行结果
因为上述算法需要迭代500次,不适合大量数据的计算
所以改进 采用随机梯度上升
即每次只用一组数据进行一次theta的更新,而不是每次都用所有的theta
改进的随机梯度上升算法
def stocGradAscent0(dataMatrix,classLabels):
#注意这里的dataMatrix是array数组不是矩阵
m,n=shape(dataMatrix)
alpha=0.01
weight=ones(n)
for i in range(m):
error=classLabels[i]-sigmoid(sum(weight*dataMatrix[i]))
weight=weight+error*alpha*dataMatrix[i]
return weight
由于这里受限于数据量的大小,对theta更新次数较少,所以不是很精确
因此人为增加更新次数,同时动态更新alpha的值
def stocGradAscent1(dataMatrix,classLabels,numIter=150):
m,n=shape(dataMatrix)
weight=ones(n)
for i in range(numIter):
dataIndex=range(m)
for j in range(m):
alpha=4.0/(1.0+i+j)
randIndex=int(random.uniform(0,len(dataIndex)))
error=classLabels[randIndex]-sigmoid(sum(weight*dataMatrix[randIndex]))
weight=weight+alpha*error*dataMatrix[randIndex]
return weight
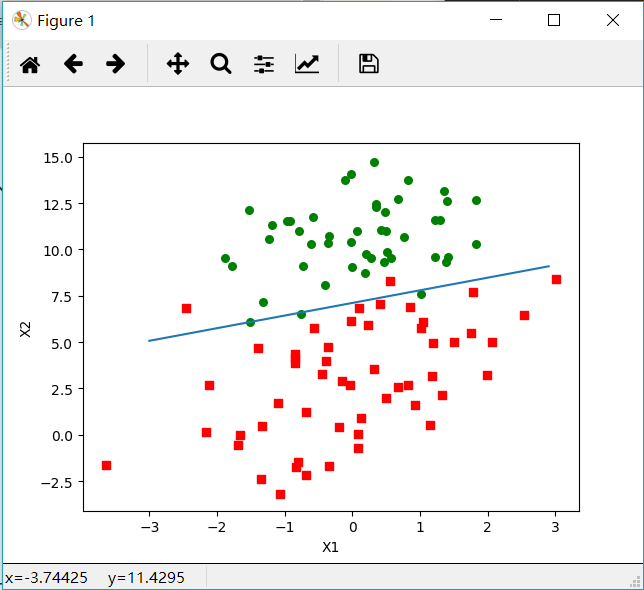
随机梯度下降算法的运行结果(结果反而比第一个好)
实战:预测马的死亡率
一、数据预处理
常用的数据预处理方法:
由于系数的计算公式:
当特征值缺失时 weight=weight 所以不会造成影响,所以置缺失的特征值为0
而缺失的标签值直接丢弃
二、进行分类
方法:将特征向量乘以训练好的系数求和,带入sigmoid函数,大于0.5则为正样本,否则为负样本
from logRegres import *
def classifyVector(inX,weight):
prob=sigmoid(sum(inX*weight))
if prob>0.5:return 1.0
else: return 0.0
def colicTest():
trainLabels =[]
trainSet=[]
with open('horseColicTraining.txt') as frTrian:
for line in frTrian.readlines():
currLine=line.strip().split('\t')
n=int(len(currLine))-1
Arr=[float(i) for i in currLine[0:n]]
trainSet.append(Arr)
trainLabels.append(float(currLine[-1]))
trianWeights=stocGradAscent1(array(trainSet),trainLabels,1000)
with open('horseColicTest.txt') as frTest:
lineArr=[]
errorCount=0.0
numTestVect = 0.0
for line in frTest.readlines():
numTestVect+=1
currline=line.strip().split('\t')
Arr=[float(i) for i in currline[0:len(currline)-1]]
lineArr.append(Arr)
if int(classifyVector(array(lineArr),trianWeights))!=int(currline[-1]):
errorCount+=1
errorRate=float(errorCount)/float(numTestVect)
print("the error rate of this test is:%f"%errorRate)
return errorRate
def multiTest():
numTests = 10; errorSum=0.0
for k in range(numTests):
errorSum += colicTest()
print("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))
multiTest()
注释:1.书上读取文件时写的代码比较繁琐,我自己用切片简化了一下。同时学习了在用切片时想进行类型转换应该 Arr=[float(i) for i in currline[0:len(currline)-1]] 这样
2.在随机梯度增加时 有一句del(dataIndex[randIndex])在python3中出错,应该将dataIndex=rand(m)改为dataIndex=list(rand(m)),这样更改之后错误率明显上升,我自己感觉这个语句的作用应该是删除已经被删选过的数据,避免重复选择一些数据进行学习,但是为什么效果更差了很奇怪,待解决