线性回归的多重共线性问题及其解决
Content
- 线性回归的多重共线性
-
- 1. 前提
- 2. 由损失函数推导ω(基于最小二乘法OLS)
- 3. 上述计算结果不成立
-
- 3.1 多重共线性的机器学习解释
- 3.2 多重共线性的解决
- 4. Ridge & Lasso
-
- 4.1 Ridge
- 4.2 Lasso
线性回归的多重共线性
1. 前提
- 线性回归的矩阵表示
y = X T × ω y\ =\ X^{T}\ \times \ \omega y = XT × ω
假如有m个训练样本,则

- 损失函数的定义
在此,我们使用最常用的损失函数SSE(平方误差)来定义线性回归的损失函数

用矩阵表示:
S S E = ( y − X ω ) T ( y − X ω ) SSE=\left( y-X\omega \right)^{T} \left( y-X\omega \right) SSE=(y−Xω)T(y−Xω)
2. 由损失函数推导ω(基于最小二乘法OLS)
根据损失函数的定义,我们在线性回归中是想让损失函数越小越好,因此我们需要用极限(求导)的方式使得损失函数取到最小值。
L l o s s = S S E = ( y − X ω ) T ( y − X ω ) L_{loss} = SSE =\left(y-X\omega \right)^{T}\left(y-X\omega \right) Lloss=SSE=(y−Xω)T(y−Xω)
d L l o s s d ω → 0 \frac{\mathrm{d} L_{loss}}{\mathrm{d} \omega} \rightarrow 0 dωdLloss→0
推导过程:
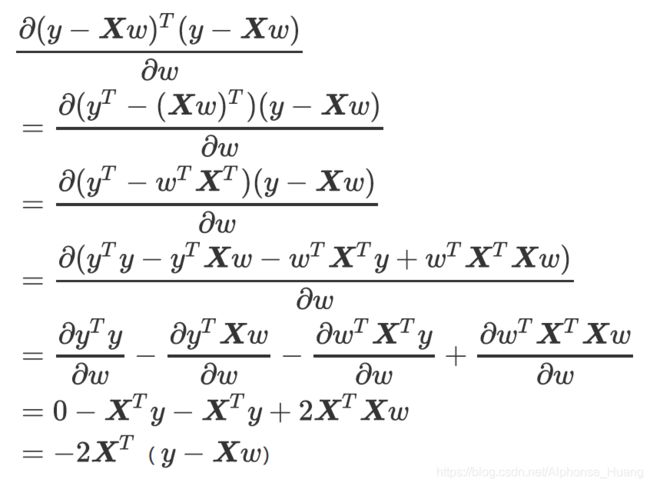
令其为0:

当 ( X T X ) − 1 可 逆 的 条 件 下 \left( X^{T}X\right)^{-1} 可逆的条件下 (XTX)−1可逆的条件下
ω = ( X T X ) − 1 X T y \omega = \left( X^{T}X\right)^{-1} X^{T}y ω=(XTX)−1XTy
3. 上述计算结果不成立
我们知道,当特征矩阵满足多重共线性的前提下,矩阵是不可逆的,此时无法用OLS来求解ω。
逆矩阵存在的条件
3.1 多重共线性的机器学习解释
从机器学习的角度来看,多重共线性是指线性模型中的特征(解释变量)之间由于存在精确相关关系或高度相关关系,多重共线性的存在会使模型无法建立,或者估计失真性。
而在现实中特征之间完全独立的情况其实非常少,因为大部分数据统计手段或者收集者并不考虑统计学或者机器学习建模时的需求,现实数据总都会存在一些相关性,极端情况下,甚至还可能出现收集的特征数量比样本数量多的情况。通常来说,这些相关性在机器学习中通常无伤大雅(在统计学中他们可能是比较严重的问题),即便有一些偏差,只要最小二乘法能够求解,我们都有可能会无视掉它。毕竟,想要消除特征的相关性,无论使用怎样的手段,都无法避免进行特征选择,这意味着可用的信息变得更加少,对于机器学习来说,很有可能尽量排除相关性后,模型的整体效果会受到巨大的打击。这种情况下,我们选择不处理相关性,只要结果好,我们就尽量无视这个问题。
然而多重共线性就不是这样一回事了,它的存在会造成模型极大地偏移,无法模拟数据的全貌,因此这是必须解决的问题。
3.2 多重共线性的解决
| 统计学先验思想 | 逐步向前回归 | 改进的线性回归 |
|---|---|---|
| 在开始建模之前先对数据进行各种相关性检验,如果存在多重共线性则可考虑对数据的特征进行删减筛查,或者使用降维算法对其进行处理,最终获得一个完全不存在相关性的数据集 | 逐步归回能够筛选对标签解释力度最强的特征,同时对于存在相关性的特征们加上⼀个惩罚项,削弱其对标签的贡献,以绕过最小二乘法对共线性较为敏感的缺陷 | 在原有的线性回归算法基础上进行修改,使其能够容忍特征列存在多重共线性的情况,并且能够顺利建模,且尽可能的保证RSS取得最小值 |
这三种手段中:
第一种相对耗时耗力,需要较多的人工操作,并且会需要混合各种统计学中的知识和检验来进行使用;
第二种手段在现实中应用较多,不过由于理论复杂,效果也不是非常高效;
逐步向前回归
我们主要使用第三种改进的线性回归。
4. Ridge & Lasso
这两个算法不是为了提升模型表现,而是为了修复漏洞(多重共线性)而设计的。
实际上,我们使用岭回归或者Lasso,模型的效果往往会下降一些,因为我们删除了一小部分信息。
4.1 Ridge
Ridge主要是将求解ω的过程转化为一个带条件的最优化问题,然后用最小二乘法求解。
Ridge在多元线性回归的损失函数上加上了正则项,表达为系数ω的L2范式乘以正则化系数α
在Ridge上,损失函数的定义为:
m i n ω ∣ ∣ X ω − y ∣ ∣ 2 2 + α ∣ ∣ ω ∣ ∣ 2 2 min_{\omega}\left| \left| X\omega -y\right| \right|^{2}_{2} +\alpha \left| \left| \omega \right| \right|^{2}_{2} minω∣∣Xω−y∣∣22+α∣∣ω∣∣22
则有

最后
ω = ( X T X + α I ) − 1 X T y \omega = \left( X^{T}X+\alpha I\right)^{-1} X^{T}y ω=(XTX+αI)−1XTy
问题转化为要求 ( X T X + α I ) \left( X^{T}X+\alpha I\right) (XTX+αI)存在逆矩阵。
我们来看其矩阵具体的表现形式:

此时方阵 X T X X^{T}X XTX是不可逆的,最小二乘法就无法使用。然而,加上 α I \alpha I αI了之后,我们的矩阵就大不一样了:

最后得到的这个行列式还是一个梯形行列式。我们讨论该行列式是否存在全0列:
若存在全0列,应该满足如下假设之一:
- α = 0 \alpha=0 α=0;
- 原本矩阵 X T X X^{T}X XTX存在某个对角元素为 − α -\alpha −α。
首先, α \alpha α的值,理论上我们是可以取无穷个的,那我们只要使得 α ≠ 0 \alpha \neq 0 α=0则上述条件1即可避免;而对于条件二,我们只要规避因为 α \alpha α的值为上述的因为 − α -\alpha −α,则该条件也可避免。
最后,通过改变正则化因子因为 α \alpha α的值,我们就可以规避线性回归中多重共线性的影响。
4.2 Lasso
和Ridge一样,Lasso是被创造来作用于多重共线性问题的算法,不过Lasso使用的是系数 ω \omega ω的L1范式(L1范式则是系数的绝对值)乘以正则化系数 α \alpha α
对于Lasso,其损失函数的表达式为
m i n ω ∣ ∣ X ω − y ∣ ∣ 2 2 + α ∣ ∣ ω ∣ ∣ 1 min_{\omega}\left| \left| X\omega -y\right| \right|^{2}_{2} +\alpha \left| \left| \omega \right| \right|^{}_{1} minω∣∣Xω−y∣∣22+α∣∣ω∣∣1
同样的,我们进行求导

最终结果为
X T X ω = X T y − α I 2 X^{T}X\omega =X^{T}y-\frac{\alpha I}{2} XTXω=XTy−2αI
在这里,我们注意到刚刚在普通线性回归中可能存在的多重共线性问题在Lasso中同样无法避免。
因此Lasso无法解决特征之间”精确相关“的问题。当我们使用最小二乘法求解线性回归时,如果线性回归无解或者报除零错误,换Lasso不能解决任何问题。
然而,在现实中我们其实会比较少遇到“精确相关”的多重共线性问题,大部分多重共线性问题应该是“高度相关“,而如果我们假设方阵 X T X X^{T}X XTX的逆是一定存在的,那我们可以有
ω = ( X T X ) − 1 ( X T y − α I 2 ) \omega =\left( X^{T}X\right)^{-1}\left( X^{T}y -\frac{\alpha I}{2} \right) ω=(XTX)−1(XTy−2αI)
通过增大 α \alpha α,我们可以为的计算增加一个负项,从而限制参数估计中的大小,而防止多重共线性引起的参数被估计过大导致模型失准的问题。
因此我们说,Lasso不是从根本上解决多重共线性问题,而是限制多重共线性带来的影响。
在此,我们发现两种算法的区别在于损失函数定义的不同,或者是L1正则化及L2正则化所带来的影响不同。
L1和L2正则化一个核心差异就是他们对系数的影响:
两个正则化都会压缩系数的大小,对标签贡献更少的特征的系数会更小,也会更容易被压缩。不过,L2正则化只会将系数压缩到尽量接近0,但L1正则化主导稀疏性,因此会将系数压缩到0。
而对于Lasso本身带有的独特性质,也为Lasso能够进行特征选择奠定了基础(下次写)。