基于python的可视化分析_Python数据的可视化分析,python

python数据可视化分析

首先载入必要的库

import warnings

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

sns.set()

warnings.filterwarnings('ignore')

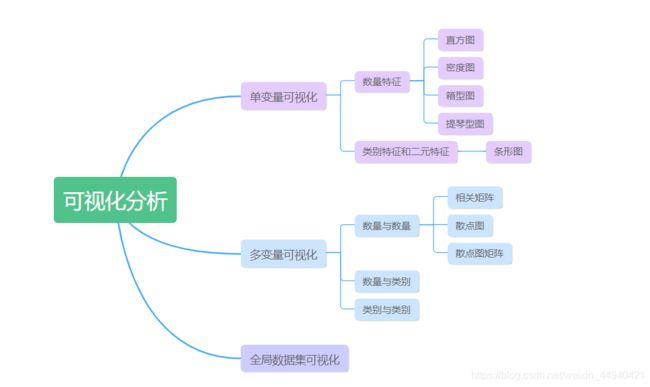
单变量可视化

单变量(univariate)分析一次只关注一个变量。当我们独立地分析一个特征时，通常最关心的是该特征值的分布情况。下面考虑不同统计类型的变量，以及相应的可视化工具。

一、数值特征

数量特征(quantitative feature)的值为有序数值。这些值可能是离散的，例如整数，也可能是连续的，例如实数。

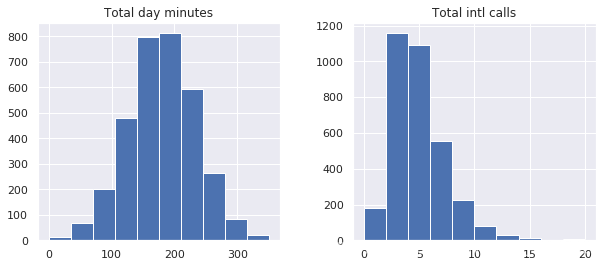
1、直方图：hist

直方图依照相等的间隔将值分组为柱，它的形状可能包含了数据分布的一些信息，如高斯分布、指数分布等。当分布总体呈现规律性，但有个别异常值时，你可以通过直方图辨认出来。

features = [‘列名1’, ‘列名2’]

df[features].hist(figsize=(10, 4))

其中figsize变量是指每张图片尺寸大小。

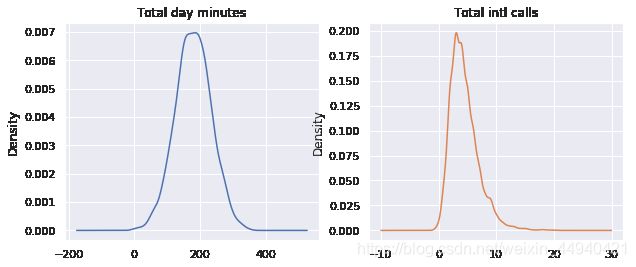
2、密度图：plot

密度图(density plots)，也叫核密度图( kernel density estimate，KDE)是理解数值变量分布的另一个方法。它可以看成是直方图平滑( smoothed )的版本。相比直方图，它的主要优势是不依赖于柱的尺寸，更加清晰。

features = [‘列名1’, ‘列名2’]

df[features].plot(kind=‘density’, subplots=True, layout=(1, 2),sharex=False, figsize=(10, 4), legend=False, title=features)

其中kind=‘density表示的是类型是密度图，layout=(1, 2)表示呈现一行两列图的格式，sharex=False表示不共享X轴，figsize变量是指每张图片尺寸大小。

当然，还可以使用 seaborn 的 distplot() 方法观测数值变量的分布。例如，Total day minutes 每日通话时长 的分布。默认情况下，该方法将同时显示直方图和密度图。

sns.distplot(df[‘列名’])

上图中直方图的柱形高度已进行归一化处理，表示的是密度而不是样本数

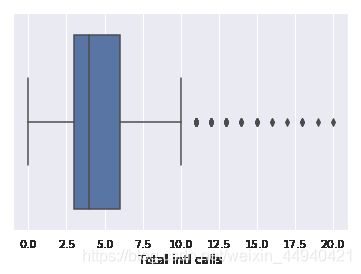
3、箱型图：boxplot()

箱形图的主要组成部分是箱子(box)，须(whisker)和一些单独的数据点(离群值)，分别简单介绍如下：

箱子显示了分布的四分位距，它的长度由 25th(Q1，下四分位数)25th(Q1，下四分位数) 和

75th(Q3，上四分位数)75th(Q3，上四分位数) 决定，箱中的水平线表示中位数 (50%50%)。

须是从箱子处延伸出来的线，它们表示数据点的总体散布，具体而言，是位于区间

(Q1−1.5⋅IQR,Q3+1.5⋅IQR)(Q1−1.5⋅IQR,Q3+1.5⋅IQR)的数据点，其中

IQR=Q3−Q1IQR=Q3−Q1，也就是四分位距。

离群值是须之外的数据点，它们作为单独的数据点，沿着中轴绘制。

sns.boxplot(x=‘列名’, data=df)

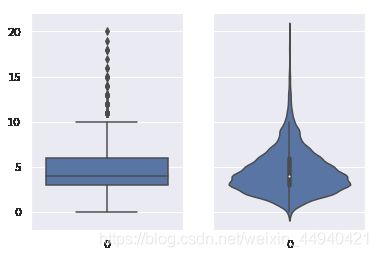
4、提琴型图：violinplot()

提琴形图和箱形图的区别是，提琴形图聚焦于平滑后的整体分布，而箱形图显示了单独样本的特定统计数据。

fig,axes = plt.subplots(1, 2, sharey=True, figsize=(6, 4))

sns.boxplot(data=df[‘列名’], ax=axes[0])

sns.violinplot(data=df[‘列名’], ax=axes[1])

其中：plt.subplots(1, 2, sharey=True, figsize=(6, 4))表示绘制多子图。

sharex, sharey：

设置为 True 或者 ‘all’ 时，所有子图共享 x 轴或者 y 轴

设置为 False or ‘none’ 时，所有子图的 x，y 轴均为独立

设置为 ‘row’ 时，每一行的子图会共享 x 或者 y 轴

设置为 ‘col’ 时，每一列的子图会共享 x 或者 y 轴

二、类别特征和二元特征

类别特征(categorical features

take)反映了样本的某个定性属性，它具有固定数目的值，每个值将一个观测数据分配到相应的组，这些组称为类别(category)。

假如某一数值特征重复值很多，因此，既可以看成数值变量，也可以看成有序类别变量。

二元(binary)特征是类别特征的特例，其可能值有 2 个。即bool类型

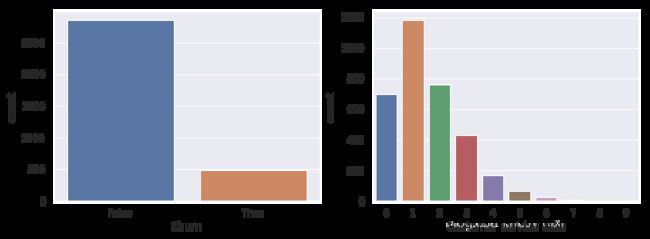
条形图：countplot()

fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12, 4))

sns.countplot(x=‘Churn’, data=df, ax=axes[0])

sns.countplot(x=‘Customer service calls’, data=df, ax=axes[1])

其中：nrows，ncols：子图的行列数

子图的行列数。

条形图和直方图的区别如下：

直方图适合查看数值变量的分布，而条形图用于查看类别特征。

直方图的 X 轴是数值；条形图的 X 轴可能是任何类型，如数字、字符串、布尔值。

直方图的 X 轴是一个笛卡尔坐标轴；条形图的顺序则没有事先定义。

多变量可视化

多变量(multivariate)图形可以在单张图像中查看两个以上变量的联系，和单变量图形一样，可视化的类型取决于将要分析的变量的类型。

一、数量与数量

1、相关矩阵

相关矩阵可揭示数据集中的数值变量的相关性。这一信息很重要，因为有一些机器学习算法(比如，线性回归和逻辑回归)不能很好地处理高度相关的输入变量。

首先要丢弃非数值变量

numerical = list(set(df.columns) -set([‘非数量值列名1’, ‘非数量值列名2’,…]))

然后计算相关系数和绘图

corr_matrix = df[numerical].corr()

sns.heatmap(corr_matrix)

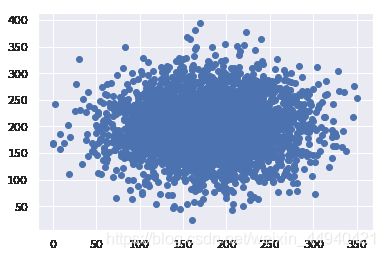
2、散点图：scatter()

散点图(scatter plot)将两个数值变量的值显示为二维空间中的笛卡尔坐标(Cartesian coordinate)。通过 matplotlib 库的 scatter() 方法可以绘制散点图

plt.scatter(df[‘列名1’], df[‘列名2’])

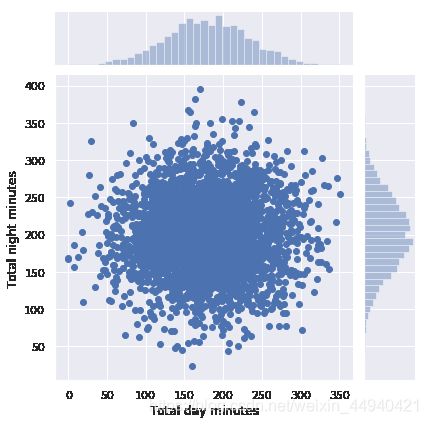
seaborn 库的 jointplot() 方法在绘制散点图的同时会绘制两张直方图，某些情形下它们可能会更有用。

sns.jointplot(x=‘列名1’, y=‘列名2’,data=df, kind=‘scatter’)

jointplot() 方法还可以绘制平滑过的散点直方图。

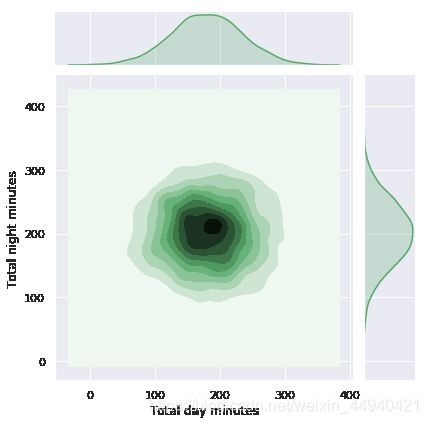
sns.jointplot(‘列名1’, ‘列名2’, data=df, kind=“kde”, color=“g”)

上图基本上就是之前讨论过的核密度图的双变量版本。

3、散点图矩阵

在某些情形下，我们可能想要绘制如下所示的散点图矩阵(scatterplot matrix)。它的对角线包含变量的分布，并且每对变量的散点图填充了矩阵的其余部分

numerical = list(set(df.columns) -set([‘非数量值列名1’, ‘非数量值列名2’,…]))

%config InlineBackend.figure_format = ‘png’

sns.pairplot(df[numerical])

二、数量和类别

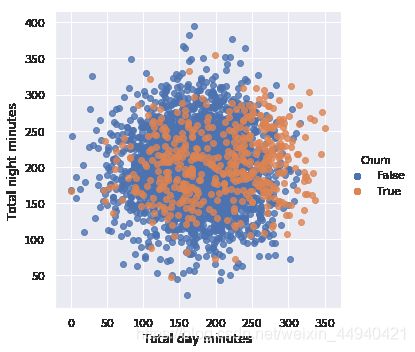
sns.lmplot(‘数量列名1’, ‘数量列名2’,data=df, hue=‘类别列名’, fit_reg=False)

三、类别和类别

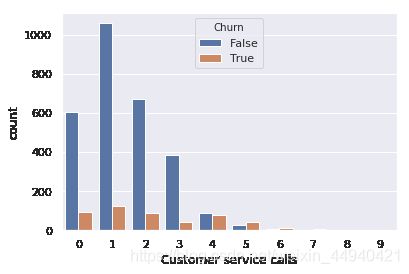
前面条形图加上hue参数即可。

sns.countplot(x=‘类别1’, hue=‘类别2’, data=df)

全局数据集可视化

上面我们一直在研究数据集的不同方面(facet)，通过猜测有趣的特征并一次选择少量特征进行可视化。如果我们想一次性显示所有特征并仍然能够解释生成的可视化，该怎么办？

通过降维：

大多数现实世界的数据集有很多特征，每一个特征都可以被看成数据空间的一个维度。因此，我们经常需要处理高维数据集，然而可视化整个高维数据集相当难。为了从整体上查看一个数据集，需要在不损失很多数据信息的前提下，降低用于可视化的维度。这一任务被称为降维(dimensionality reduction)。降维是一个无监督学习(unsupervised learning)问题，因为它需要在不借助任何监督输入(如标签)的前提下，从数据自身得到新的低维特征。

2种降维方法：

PCA：主成分分析(Principal Component Analysis, PCA)是一个著名的降维方法，但主成分分析的局限性在于，它是线性(linear)算法，这意味着对数据有某些特定的限制。

t-SNE：与线性方法相对的，有许多非线性方法，统称流形学习(Manifold Learning)。著名的流形学习方法之一是 t-SNE。

关于t-SNE：

它的基本思路很简单：为高维特征空间在二维平面(或三维平面)上寻找一个投影，使得在原本的 n 维空间中相距很远的数据点在二维平面上同样相距较远，而原本相近的点在平面上仍然相近。

步骤：

该数据库创建一个 t-SNE 表示，首先加载依赖。

from sklearn.manifold import TSNE

from sklearn.preprocessing import StandardScaler

去除 State 州 和 Churn 离网率 变量，然后用 pandas.Series.map() 方法将二元特征的「Yes」/「No」转换成数值。

(将其他文本特征和目标特征去除)

X = df.drop(['Churn', 'State'], axis=1)

X['International plan'] = X['International plan'].map({'Yes': 1, 'No': 0})

X['Voice mail plan'] = X['Voice mail plan'].map({'Yes': 1, 'No': 0})

使用 StandardScaler() 方法来完成归一化数据，即从每个变量中减去均值，然后除以标准差。

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

现在可以构建 t-SNE 表示了。

tsne = TSNE(random_state=17)

tsne_repr = tsne.fit_transform(X_scaled)

然后以图形的方式可视化

plt.scatter(tsne_repr[:, 0], tsne_repr[:, 1], alpha=.5)

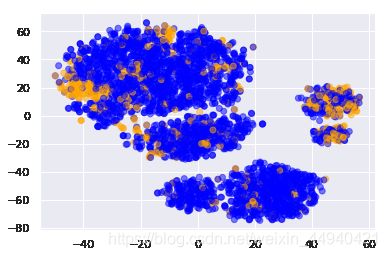
根据离网情况给 t-SNE 表示加上色彩(蓝色表示忠实用户，黄色表示不忠实用户)，形成离网情况散点图

plt.scatter(tsne_repr[:, 0], tsne_repr[:, 1],

c=df['Churn'].map({False: 'blue', True: 'orange'}), alpha=.5)

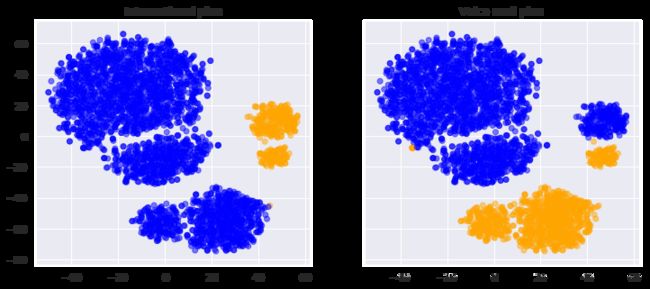
可以看到，离网客户集中在低维特征空间的一小部分区域。为了更好地理解这一图像，可以使用剩下的两个二元特征，即 International plan 国际套餐 和 Voice mail plan 语音邮件套餐 给图像着色，蓝色代表二元特征的值为 Yes，黄色代表二元特征的值为 No。

_, axes = plt.subplots(1, 2, sharey=True, figsize=(12, 5))

for i, name in enumerate(['International plan', 'Voice mail plan']):

axes[i].scatter(tsne_repr[:, 0], tsne_repr[:, 1],

c=df[name].map({'Yes': 'orange', 'No': 'blue'}), alpha=.5)

axes[i].set_title(name)

最后，了解下 t-SNE 的缺陷

计算复杂度高。如果你有大量样本，你应该使用 Multicore-TSNE

随机数种子的不同会导致图形大不相同，这给解释带来了困难。通常而言，你不应该基于这些图像做出任何决定性的结论，因为它可能和单纯的猜测差不多。当然，t-SNE 图像中的某些发现可能会启发一个想法，这个想法可以通过更全面深入的研究得到确认。