一、概述
(1)聚类分析
目标是,分组数据使得,组内的对象是相似的(相关的),不同组是不同的(不相关的)。
(2)聚类类型
1、层次、划分
层次聚类(嵌套聚类,hierarchial clustering):聚类簇组织成一棵树,每一个结点是其子女的并。
划分聚类(非嵌套聚类,partional clustering):简单的将数据对象划分为不重叠的子集。
2、互斥、重叠、模糊
互斥聚类(exclusive):每个对象被指派到单独的单个簇。
重叠聚类(overlapping):一个对象可以同时属于多个簇。
模糊聚类(fuzzy clustering):概率聚类,每个对象以0-1之间的的权值隶属于一个类,但是每个对象的权值之和为1。
3、完全、部分
完全聚类(complete clustering):每个对象指派到一个类。
部分聚类(partial clustering):某些对象可以不属于明确定义的类。
(3)簇类型
下面显示一些簇类型:
类型:明显分离、基于原型(中心簇)、基于图(连通)、基于密度、共同性质的(概念簇)。
二、K-均值
(1)基本K-均值算法
算法步骤:
目标函数:
^{2}, c_{i}=\frac{1}{m_{i}}\sum_{x\in C_{i}}x)
上面的第3、4步骤试图最小化目标函数(SSE或者其他的),直到收敛。
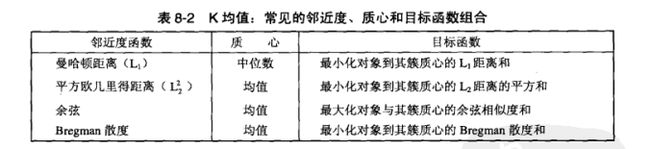
常见的邻近度和目标函数组合:
初始质心:
不同的初始质心会收敛到不同的结果。
随机初始质心:问题是,即使运行多次也不一定能得到好的分类。因为,一旦一个簇内有多个质心,该簇很可能被分裂。
其他方法:先使用层次聚类,从中提取K个类,使用这K个类的质心作为初始质心。仅对:样本较小,K较小有效。
(2)K均值:附加问题
处理空簇
所有的点没有一个分配到一个质心。选择替补质心。
离群点
离群点对于k-均值聚类有较大影响,应该删除。
后处理SSE
增加簇:
分裂一个簇:选择SSE最大的分裂。
引进一个新的质心:选择离所有质心最远的点。
减少簇:
拆散一个簇:删除簇的对应质心。簇中的点重新分配。
合并两个簇:选择两个质心最接近的两个簇合并。
增量的更新质心
给定一个目标函数,每步要零次或两次更新质心。
可能产生次序依赖性问题,开销也稍微大一些。
(3)二分K均值
思路:
为了得到 K 个簇,将所有点分裂成两个簇,从这些簇中,选取一个继续分裂,直到产生 K 个簇。
算法:
带分裂的簇选择方法有很多:最大的簇,最大SSE的簇等。
(4)优点与缺点
优点:二分K均值,不太受初始值的影响。
缺点:不能处理非球形簇、不同尺寸、不同密度的簇。
三、凝聚层次聚类
(1)基本算法
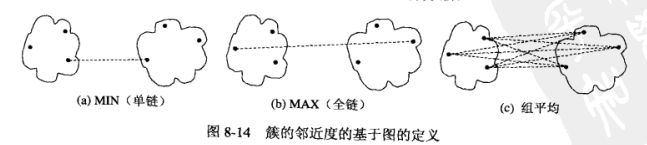
(2)距离的度量:
最短距离(min)、最长距离(max)、平均距离、ward和质心距离
(3)簇邻近度的Lance-Williams公式
Lance-Williams公式:
=\alpha_{A}p(A,Q)+ \alpha_{B}p(B,Q)+\beta p(A,B)+\gamma |p(A,Q)-p(B,Q)|)
A、B、Q合并得到R。p(. , .)是邻近度函数,以上表示它们为线性函数。
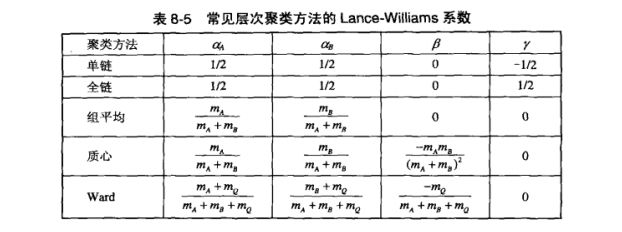
下面是Lance-Williams公式鱼邻近度函数的对应:
(4)层次聚类的问题
1、缺乏全局目标函数:避开了解决困难的组合优化问题,很难选择初始点的问题。
2、合并是最终的:一旦合并就不能撤销。
四、DBSCAN
基于密度聚类算法,寻找被低密度区域分离的高密度区域。
(1)传统密度:基于中心的方法
核心点(core point):该点给定邻域的点个数超过用户给定阈值 MinPts(Eps为用户定义的距离)。A点。
边界点(border point):不是核心点,它落在某个核心点邻域。B点。
噪声点(noise point):即非核心点也非边界点。C点。
(2)DBSCAN算法
思路:
任意两个足够近(Eps之内)的核心点将方到一个簇中。
任何与核心点足够近的边界点放到相同簇中(如果边界点靠近不同簇的核心点,要解决平均问题)。
噪声点丢弃。
算法步骤:
选择 Eps 和 MinPts
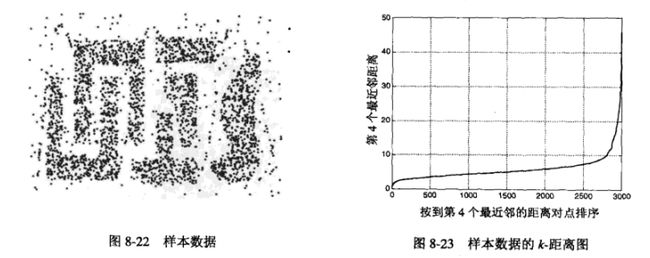
使用 k-距离
k-最近邻的距离,对于某个k,计算所有点的k-距离,以递增排序,则k-距离会在某个部分急剧变化(噪声点的k-距离很大)。选取k为MinPts,合适的距离为Eps。
下面为,使用Eps=10,MinPts=4的结果:
(3)优点与缺点
优点:对抗噪音的能力很强,能够处理任意形状和大小的簇。
缺点:DBSCAN当计算近邻的时候,开销很大。
五、簇评估
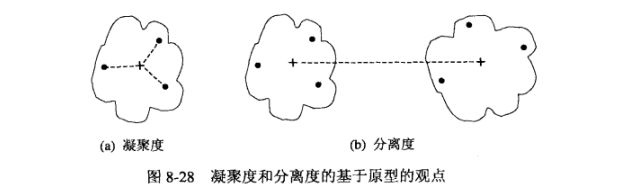
(1)非监督簇评估:凝聚度、分离度
)
K个簇的有效性,为个体簇的有效性加权和,下面给出度量表:
1、基于图:凝聚度、分离度
proximity函数可以是相似度、相异度,或者是这些量的简单函数:
=\sum_{x\in C_{i},y\in C_{i}}proximity(x,y))
=\sum_{x\in C_{i},y\in C_{j}}proximity(x,y))
2、基于原型:凝聚度、分离度
ci是Ci的原型(质心),c是总体原型(质心):
=\sum_{x\in C_{i}}proximity(x,c_{i}))
=proximity(c_{i},c_{j}))
=proximity(c_{i},c))
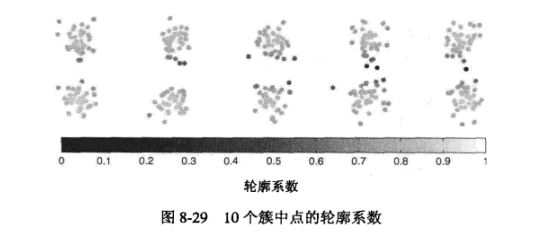
3、轮廓系数
轮廓系数(silhouette coefficient):
1、对于第 i 个对象,计算它到所在簇所有点的平均距离:ai
2、对于第 i 个对象,计算它到不含它的其他簇所有对象的平均距离,找出最小的:bi
3、对于第 i 个对象,轮廓系数为:
}{max(a_{i},b_{i})})
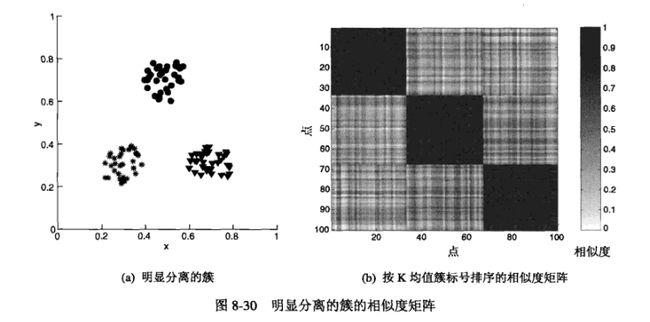
(3)非监督簇评估:近邻矩阵
可以使用某个距离度量法来度量相似度,得到每个点的距离,汇总得到近邻矩阵。但是仅使用于小数据、抽样。
(4)簇个数
使用 SSE 和轮廓系数来判断,统计上的 SSE 的说明性更强,统计上不止这一个系数可以分类。
(5)聚类趋势
度量空间中的点是否为随机分布的,使用Hopkins统计量: