重复高斯勒让德法则(gauss-legendre)求积分(python,数值积分)
第四十一篇 高斯勒让德法则
牛顿-科特斯法则很方便使用,因为样本点在积分范围内均匀分布,而且权重系数很容易记住(至少到辛普森法则)。详情可见重复牛顿-科特斯法则
高斯法则采取样本点在积分范围内的最佳间隔,并且实现给定样本点更高的精度。这些优化后的样本点的位置仍然是在积分范围内以中间点对称,但是它们的位置不是很明显,而且确实很难记住。但这些数据可以存储在子程序库中。
在高斯规则中,之前使用的求和法仍然适用,因此
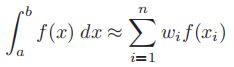
然而,当使用多项式代换然后应用高斯法则时,不仅wi,而且xi最初被视为未知数。为了求解2n次方程,必须使用f(x)精确到2n−1次的阶数。这与等效牛顿-科特斯法则相比有了很大的改进,后者在相同的采样点数下,只适用于f(x)阶数为n−1次(或当n是奇数且大于1时为n)。
高斯法则有多种类型,但最重要和使用最广泛的是高斯-勒让德法则,首先介绍这种类型。
这个法则的兴起在于考虑了±1上下限的正交化而得到简化和推广,而不是如上式所示的a和b的上下限。对于Newton-Cotes规则也考虑了类似的方法,得出了上篇的表。这样的变化不会对问题求解有任何影响,因为对应于实际区间的解可以很容易地通过一个简单的变换得到。
下面将描述Gauss-Legendre家族的前几个成员,从最简单的方法开始,即通常所说的中点法则开始。
中点法则
如果仅仅使用函数的一个点为参考点,显然,这个点适合在积分范围的中间,如下图所示。
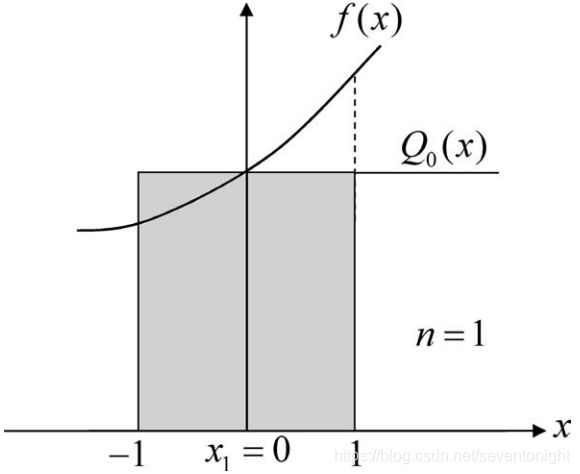
函数f(x)近似于Q0(x), Q0(x)平行于x轴,与要在区间中点积分的函数相吻合。对于f(x)的阶数为1,它的形式是

计算实例
使用中点法则去计算下面积分
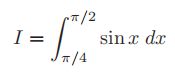
虽然积分的上下限不是±1,但我们可以通过简单的x坐标变换,乘以加权系数缩放来解决问题。样本点在积分范围的中点,加权系数等于积分范围

因此

精确解为0.7071
与矩形规则相比(矩形规则给出0.5554),中点规则以最佳样本点的位置得出了一个明显改进的结果,尽管两种方法涉及的计算量相同。
两点高斯勒让德法则(n=2)
在这种情况下,我们不知道样本点的最佳位置在哪里,所以我们将使用多项式代换法来求解他们。
这个公式是这样的
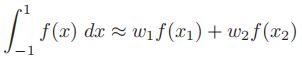
它包含4 (2n)个未知数,w1 x1 w2 x2。为了生成四个方程来解这些值,假设上面的方程为容易求得的f(x) = 1, f(x) = x, f(x) = x2和f(x) = x3。
令f(x)=1,因此
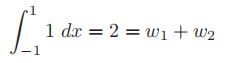
令f(x)=x,因此
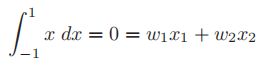
令f(x)=x2,因此

令f(x)=x3,因此

从上面第一个和第三个方程可以得到
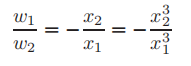
因此
![]()
假设样本点是不重合的,得到x2 =−x1
![]()
最后从方程得
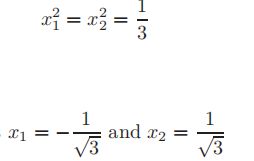
因此,积分上下限正交化的两点法则可以写成
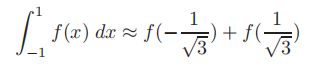
对于3次多项式f(x)是精确的。该方法实际是下图所示在x =±√13处与f(x)重合的线性函数Q1(x)下的面积。

计算实例
使用2点高斯勒让德法则计算下面积分
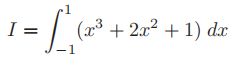
这个问题是积分的正交化形式求解,因此可以直接应用权值和样本点,从而
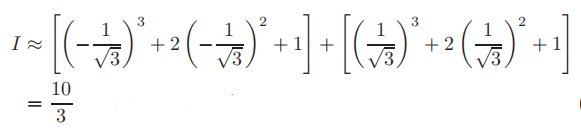
两点Gauss-Legendre法则能够精确地对立方式进行积分。为了精确地用牛顿-柯特法则积分一个三次方式,需要使用三个样本点的辛普森法则。
三点高斯勒让德法则(n=3)
这个法则采取下面的形式
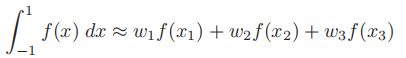
对于f(x)得分阶数为 (2n−1)= 5是来说是准确的。虽然上面方程中有6个未知数,需要对f(x)进行5次多项式替换,但可以利用对称性的特点减少方程的数量。与Newton-Cotes规则一样,加权系数和样本点对于积分范围的中点总是对称的,因此可以得出

下面将直接给出数据值,感兴趣的读者可以自行代入方程求解
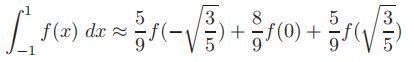
下图显示这个法则的三个样本点的位置。与之前的模式相同,实际的积分是在一个二阶多项式Q2(x)(图中未显示)下进行的,该多项式在三个样本点上上与f(x)重合。

描述了高斯勒让德家族的前三个成员,在下表中将它们与家族的后两个成员(n = 5)汇总在一起。这种方法之所以被称为高斯勒让德,是因为样本点是勒让德多项式的根


改变积分的上下限
本节描述的所有高斯勒让德都采用±1的上下限。正常情况下,通常选择在其他上下限之间积分函数,因此为了使用正交化权值和样本点,需要转换我们的问题。通过变量的变换我们可以把完成正交化的转化
得出与原问题相同的解决方案
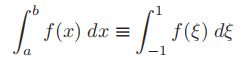
为了实现这种转换,进行下面的替换

和
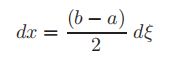
一旦问题以这种方式转化,就可以应用熟悉的高斯-勒让德权值和样本点。
计算实例
通过改变变量的方法,使用三点高斯勒让德法则计算下面的积分

由于极限不是±1,首先必须通过上面的方程进行替换来解决问题,因此

替换之后,问题变成

可以使用上面表格中的权值和样本点直接求解。可以得出

精确解-5.0626
结果相当准确;但是,由于被积分的函数是超越函数,不能用常规的法则来精确积分。
另一种正交化的方法是将样本点对称地分布在范围的中点附近。该方法不改变变量,保持了积分的原始上下限。权重则需要进行一定程度的缩放,使它们加起来等于实际的积分范围。任何给定规则的正交化权值之和总是2,因此对于这种一般的情况,这些正交化值必须乘以积分范围的一半值。对上面的算例使用这种规则求解。
计算实例
使用三点高斯勒让德的样本点和权重值去计算下面积分

如下图所示,样本点按照上下限区间的一定比例分配。
对于n = 3,使用公式三样本点的值,正交化样本点的值为

而正交化权值为

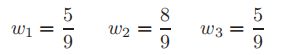
为了得到实际的样本点,将正交化样本点乘以积分范围的一半,即3/2,并以中心点为远点,所以实际的坐标为5/2。正交化权值也要乘以积分范围的一半,这样它们加起来就等于这个范围,即3。
因此,实际样本点为
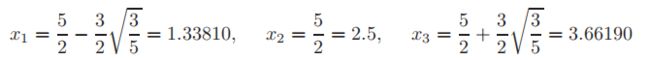
实际的权重是
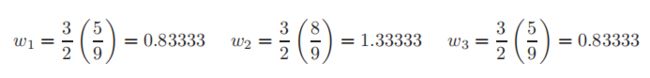
所需的积分得

精确解为-5.0626
程序如下
其中分为一个主程序和一个高斯勒让德正交的样本点和权重值得子程序gauss_legendre
#重复g高斯勒让德法则
import numpy as np
import math
import B
a=1;b=4;nsp=3;nr=2
samp=np.zeros((nsp,1))
wt=np.zeros((nsp))
B.gauss_legendre(samp,wt)
wr=(b-a)/nr
hr=0.5*wr
area=0
def f62(x):
f62=x*math.cos(x)
return f62
for i in range(1,nr+1):
cr=a+(i-1)*wr+hr
for j in range(1,nsp+1):
area=area+wt[j-1]*hr*f62(cr+samp[j-1,0]*hr)
print('重复高斯勒让德法则')
print('积分上下限',a,b)
print('牛顿柯特法则的样本点个数',nsp)
print('重复小区间个数',nr)
print('计算结果','{:13.4e}'.format(area))
gauss_legendre
def gauss_legendre(samp,wt):
nsp=samp.shape[0]
ndim=samp.shape[1]
if ndim==1:
if nsp==1:
samp[0,0]= 0.0
wt[0] = 2.0
elif nsp==2:
samp[0,0]= -0.57735026918962576449
samp[1,0]= 0.57735026918962576449
wt[0]= 1.0
wt[1]= 1.0
elif nsp==3:
samp[0,0]= -0.77459666924148337704
samp[1,0]= 0.0
samp[2,0]= 0.77459666924148337704
wt[0]= 0.55555555555555555556
wt[1]= 0.88888888888888888889
wt[2]= 0.55555555555555555556
elif nsp==4:
samp[0,0]= -0.86113631159405257524
samp[1,0]= -0.33998104358485626481
samp[2,0]= 0.33998104358485626481
samp[3,0]= 0.86113631159405257524
wt[0]= 0.34785484513745385737
wt[1]= 0.65214515486254614271
wt[2]= 0.65214515486254614271
wt[3]= 0.34785484513745385737
elif nsp==5:
samp[0,0]= -0.90617984593866399282
samp[1,0]= -0.53846931010568309105
samp[2,0]= 0.0
samp[3,0]= 0.53846931010568309105
samp[4,0]= 0.90617984593866399282
wt[0]= 0.23692688505618908751
wt[1]= 0.47862867049936646804
wt[2]= 0.56888888888888888889
wt[3]= 0.47862867049936646804
wt[4]= 0.23692688505618908751
else:
print('积分点数量错误')
elif ndim==2:
if nsp==1:
samp[0,0]= 0.0
samp[0,1]= 0.0
wt[0]= 4.0
elif nsp==4:
samp[0,0]= -0.57735026918962576449
samp[1,0]= 0.57735026918962576449
samp[2,0]= -0.57735026918962576449
samp[3,0]= 0.57735026918962576449
samp[0,1]= -0.57735026918962576449
samp[1,1]= -0.57735026918962576449
samp[2,1]= 0.57735026918962576449
samp[3,1]= 0.57735026918962576449
wt[0]= 1.0
wt[1]= 1.0
wt[2]= 1.0
wt[3]= 1.0
elif nsp==9:
samp[0,0]= -0.77459666924148337704
samp[1,0]= 0.0
samp[2,0]= 0.77459666924148337704
samp[3,0]= -0.77459666924148337704
samp[4,0]= 0.0
samp[5,0]= 0.77459666924148337704
samp[6,0]= -0.77459666924148337704
samp[7,0]= 0.0
samp[8,0]= 0.77459666924148337704
samp[0,1]= -0.77459666924148337704
samp[1,1]= -0.77459666924148337704
samp[2,1]= -0.77459666924148337704
samp[3,1]= 0.0
samp[4,1]= 0.0
samp[5,1]= 0.0
samp[6,1]= 0.77459666924148337704
samp[7,1]= 0.77459666924148337704
samp[8,1]= 0.77459666924148337704
wt[0] = 0.30864197530864197531
wt[1] = 0.49382716049382716049
wt[2] = 0.30864197530864197531
wt[3] = 0.49382716049382716049
wt[4] = 0.79012345679012345679
wt[5] = 0.49382716049382716049
wt[6] = 0.30864197530864197531
wt[7] = 0.49382716049382716049
wt[8] = 0.30864197530864197531
elif nsp==16:
samp[0,0] =-0.86113631159405257524
samp[1,0] =-0.33998104358485626481
samp[2,0] = 0.33998104358485626481
samp[3,0] = 0.86113631159405257524
samp[4,0] =-0.86113631159405257524
samp[5,0] =-0.33998104358485626481
samp[6,0] = 0.33998104358485626481
samp[7,0] = 0.86113631159405257524
samp[8,0] =-0.86113631159405257524
samp[9,0]=-0.33998104358485626481
samp[10,0]= 0.33998104358485626481
samp[11,0]= 0.86113631159405257524
samp[12,0]=-0.86113631159405257524
samp[13,0]=-0.33998104358485626481
samp[14,0]= 0.33998104358485626481
samp[15,0]= 0.86113631159405257524
samp[0,1] =-0.86113631159405257524
samp[1,1] =-0.86113631159405257524
samp[2,1] =-0.86113631159405257524
samp[3,1] =-0.86113631159405257524
samp[4,1] =-0.33998104358485626481
samp[5,1] =-0.33998104358485626481
samp[6,1] =-0.33998104358485626481
samp[7,1] =-0.33998104358485626481
samp[8,1] = 0.33998104358485626481
samp[9,1]= 0.33998104358485626481
samp[10,1]= 0.33998104358485626481
samp[11,1]= 0.33998104358485626481
samp[12,1]= 0.86113631159405257524
samp[13,1]= 0.86113631159405257524
samp[14,1]= 0.86113631159405257524
samp[15,1]= 0.86113631159405257524
wt[0]= 0.12100299328560200551
wt[1]= 0.22685185185185185185
wt[2]= 0.22685185185185185185
wt[3]= 0.12100299328560200551
wt[4]= 0.22685185185185185185
wt[5]= 0.42529330301069429082
wt[6]= 0.42529330301069429082
wt[7]= 0.22685185185185185185
wt[8]= 0.22685185185185185185
wt[9]= 0.42529330301069429082
wt[10]= 0.42529330301069429082
wt[11]= 0.22685185185185185185
wt[12]= 0.12100299328560200551
wt[13]= 0.22685185185185185185
wt[14]= 0.22685185185185185185
wt[15]= 0.12100299328560200551
elif nsp==25:
samp[0,0] =-0.90617984593866399282
samp[1,0] =-0.53846931010568309105
samp[2,0] = 0.0
samp[3,0] = 0.53846931010568309105
samp[4,0] = 0.90617984593866399282
samp[5,0] =-0.90617984593866399282
samp[6,0] =-0.53846931010568309105
samp[7,0] = 0.0
samp[8,0] = 0.53846931010568309105
samp[9,0]= 0.90617984593866399282
samp[10,0]=-0.90617984593866399282
samp[11,0]=-0.53846931010568309105
samp[12,0]= 0.0
samp[13,0]= 0.53846931010568309105
samp[14,0]= 0.90617984593866399282
samp[15,0]=-0.90617984593866399282
samp[16,0]=-0.53846931010568309105
samp[17,0]= 0.0
samp[18,0]= 0.53846931010568309105
samp[19,0]= 0.90617984593866399282
samp[20,0]=-0.90617984593866399282
samp[21,0]=-0.53846931010568309105
samp[22,0]= 0.0
samp[23,0]= 0.53846931010568309105
samp[24,0]= 0.90617984593866399282
samp[0,1] =-0.90617984593866399282
samp[1,1] =-0.90617984593866399282
samp[2,1] =-0.90617984593866399282
samp[3,1] =-0.90617984593866399282
samp[4,1] =-0.90617984593866399282
samp[5,1] =-0.53846931010568309105
samp[6,1] =-0.53846931010568309105
samp[7,1] =-0.53846931010568309105
samp[8,1] =-0.53846931010568309105
samp[9,1]=-0.53846931010568309105
samp[10,1]= 0.0
samp[11,1]= 0.0
samp[12,1]= 0.0
samp[13,1]= 0.0
samp[14,1]= 0.0
samp[15,1]= 0.53846931010568309105
samp[16,1]= 0.53846931010568309105
samp[17,1]= 0.53846931010568309105
samp[18,1]= 0.53846931010568309105
samp[19,1]= 0.53846931010568309105
samp[20,1]= 0.90617984593866399282
samp[21,1]= 0.90617984593866399282
samp[22,1]= 0.90617984593866399282
samp[23,1]= 0.90617984593866399282
samp[24,1]= 0.90617984593866399282
wt[0] = 0.05613434886242863595
wt[1] = 0.1134
wt[2] = 0.13478507238752090312
wt[3] = 0.1134
wt[4] = 0.05613434886242863595
wt[5] = 0.1134
wt[6] = 0.22908540422399111713
wt[7] = 0.27228653255075070182
wt[8] = 0.22908540422399111713
wt[9]= 0.1134
wt[10]= 0.13478507238752090305
wt[11]= 0.27228653255075070171
wt[12]= 0.32363456790123456757
wt[13]= 0.27228653255075070171
wt[14]= 0.13478507238752090305
wt[15]= 0.1134
wt[16]= 0.22908540422399111713
wt[17]= 0.27228653255075070182
wt[18]= 0.22908540422399111713
wt[19]= 0.1134
wt[20]= 0.05613434886242863595
wt[21]= 0.1134
wt[22]= 0.13478507238752090312
wt[23]= 0.1134
wt[24]= 0.05613434886242863595
else:
print('积分点数量错误')
elif ndim==3:
if nsp==1:
samp[0,0]= 0.0
samp[0,1]= 0.0
samp[0,2]= 0.0
wt[0]= 8.0
elif nsp==8:
samp[0,0]=-0.57735026918962576449
samp[1,0]= 0.57735026918962576449
samp[2,0]=-0.57735026918962576449
samp[3,0]= 0.57735026918962576449
samp[4,0]=-0.57735026918962576449
samp[5,0]= 0.57735026918962576449
samp[6,0]=-0.57735026918962576449
samp[7,0]= 0.57735026918962576449
samp[0,1]=-0.57735026918962576449
samp[1,1]=-0.57735026918962576449
samp[2,1]=-0.57735026918962576449
samp[3,1]=-0.57735026918962576449
samp[4,1]= 0.57735026918962576449
samp[5,1]= 0.57735026918962576449
samp[6,1]= 0.57735026918962576449
samp[7,1]= 0.57735026918962576449
samp[0,2]=-0.57735026918962576449
samp[1,2]=-0.57735026918962576449
samp[2,2]= 0.57735026918962576449
samp[3,2]= 0.57735026918962576449
samp[4,2]=-0.57735026918962576449
samp[5,2]=-0.57735026918962576449
samp[6,2]= 0.57735026918962576449
samp[7,2]= 0.57735026918962576449
wt[0]= 1.0
wt[1]= 1.0
wt[2]= 1.0
wt[3]= 1.0
wt[4]= 1.0
wt[5]= 1.0
wt[6]= 1.0
wt[7]= 1.0
elif nsp==27:
samp[0,0]= -0.77459666924148337704
samp[1,0]= 0.0
samp[2,0]= 0.77459666924148337704
samp[3,0]= -0.77459666924148337704
samp[4,0]= 0.0
samp[5,0]= 0.77459666924148337704
samp[6,0]= -0.77459666924148337704
samp[7,0]= 0.0
samp[8,0]= 0.77459666924148337704
samp[9,0]=-0.77459666924148337704
samp[10,0]= 0.0
samp[11,0]= 0.77459666924148337704
samp[12,0]=-0.77459666924148337704
samp[13,0]= 0.0
samp[14,0]= 0.77459666924148337704
samp[15,0]=-0.77459666924148337704
samp[16,0]= 0.0
samp[17,0]= 0.77459666924148337704
samp[18,0]=-0.77459666924148337704
samp[19,0]= 0.0
samp[20,0]= 0.77459666924148337704
samp[21,0]=-0.77459666924148337704
samp[22,0]= 0.0
samp[23,0]= 0.77459666924148337704
samp[24,0]=-0.77459666924148337704
samp[25,0]= 0.0
samp[26,0]= 0.77459666924148337704
samp[0,1]= -0.77459666924148337704
samp[1,1]= -0.77459666924148337704
samp[2,1]= -0.77459666924148337704
samp[3,1]= -0.77459666924148337704
samp[4,1]= -0.77459666924148337704
samp[5,1]= -0.77459666924148337704
samp[6,1]= -0.77459666924148337704
samp[7,1]= -0.77459666924148337704
samp[8,1]= -0.77459666924148337704
samp[9,1]= 0.0
samp[10,1]= 0.0
samp[11,1]= 0.0
samp[12,1]= 0.0
samp[13,1]= 0.0
samp[14,1]= 0.0
samp[15,1]= 0.0
samp[16,1]= 0.0
samp[17,1]= 0.0
samp[18,1]= 0.77459666924148337704
samp[19,1]= 0.77459666924148337704
samp[20,1]= 0.77459666924148337704
samp[21,1]= 0.77459666924148337704
samp[22,1]= 0.77459666924148337704
samp[23,1]= 0.77459666924148337704
samp[24,1]= 0.77459666924148337704
samp[25,1]= 0.77459666924148337704
samp[26,1]= 0.77459666924148337704
samp[0,2]= -0.77459666924148337704
samp[1,2]= -0.77459666924148337704
samp[2,2]= -0.77459666924148337704
samp[3,2]= 0.0
samp[4,2]= 0.0
samp[5,2]= 0.0
samp[6,2]= 0.77459666924148337704
samp[7,2]= 0.77459666924148337704
samp[8,2]= 0.77459666924148337704
samp[9,2]=-0.77459666924148337704
samp[10,2]=-0.77459666924148337704
samp[11,2]=-0.77459666924148337704
samp[12,2]= 0.0
samp[13,2]= 0.0
samp[14,2]= 0.0
samp[15,2]= 0.77459666924148337704
samp[16,2]= 0.77459666924148337704
samp[17,2]= 0.77459666924148337704
samp[18,2]=-0.77459666924148337704
samp[19,2]=-0.77459666924148337704
samp[20,2]=-0.77459666924148337704
samp[21,2]= 0.0
samp[22,2]= 0.0
samp[23,2]= 0.0
samp[24,2]= 0.77459666924148337704
samp[25,2]= 0.77459666924148337704
samp[26,2]= 0.77459666924148337704
wt[0] = 0.17146776406035665295
wt[1] = 0.27434842249657064472
wt[2] = 0.17146776406035665295
wt[3] = 0.27434842249657064472
wt[4] = 0.43895747599451303155
wt[5] = 0.27434842249657064472
wt[6] = 0.17146776406035665295
wt[7] = 0.27434842249657064472
wt[8] = 0.17146776406035665295
wt[9] = 0.27434842249657064472
wt[10] = 0.43895747599451303155
wt[11] = 0.27434842249657064472
wt[12] = 0.43895747599451303155
wt[13] = 0.70233196159122085048
wt[14] = 0.43895747599451303155
wt[15] = 0.27434842249657064472
wt[16] = 0.43895747599451303155
wt[17] = 0.27434842249657064472
wt[18] = 0.17146776406035665295
wt[19] = 0.27434842249657064472
wt[20] = 0.17146776406035665295
wt[21] = 0.27434842249657064472
wt[22] = 0.43895747599451303155
wt[23] = 0.27434842249657064472
wt[24] = 0.17146776406035665295
wt[25] = 0.27434842249657064472
wt[26] = 0.17146776406035665295
else:
print('积分点数量错误')
else:
print('维度不合理')