13.2 Question Answering 问答系统意境级讲解

上半部分： 13.1Question Answering 问答系统意境级讲解_炫云云-CSDN博客

将学习更为复杂、各式各样的QA中Question问题的部分。

我们将会学习到三种由简及难的问题类型及其对应解法：

第一类：匹配+抽取式问题
第二类：复杂的推理问题
第三类：对话问答

一、QA1 匹配+抽取式问题

1、数据集

$$图1$$

在此，如图 1，举一个SQuAD中标准的示例，在机器读取文章后，根据问题中比较重要的词汇对文章进行匹配，即相同的词汇在文章和问题中均出现了，找出其出现段落。再在段落中进行答案的抽取。

那像这样的简单匹配抽取式问题该怎么用神经网络去做呢？

2、问题对文章的注意力 Query-to-context Attention

第一版

$$图2$$

一个经典的做法就是使用问题到文章的Attention机制，具体做法如上图，首先，预处理文章Knowledge source得到每个token的词向量表示，问题部分如法炮制，将问题浓缩成一个向量。接下来，实现匹配就用Attention，其实在此做Attention就是相当于将问题的向量与文章中每个token的词向量做相似度计算，也就是匹配。然后，将每一个Attention得到的权重参数与对应token相乘求和，也就是抽取，得到代表答案的一个向量。

Attention的计算：

5.1注意力机制 Attention is all you need

注意的是，这里加权求和不是用的蓝色计算attention的向量，而是用绿色的向量，这个向量也是蓝色模型抽取出来的另外一组vector。加权求和得到的结果再丢到answer模块中进行计算。如果是bAbI那种任务就是用classifier进行分类，如果是SQuAD则用predict来预测答案对应的时间步。

$$图3$$

具体模型有：End-to-end Memory Network这个模型的思路和上面讲的大概相同，橙色对应上面的绿色向量用来求和，蓝色对应上面的蓝色向量用来求权重，最后做的bAbI任务，所以是分类。

End-to-end Memory Network请看： 5.10 Memory Networks 记忆网络的应用与方法

第二版

$$图4$$

第二版将question分成多个vector，每一个vector都和source的embedding做attention，上图有三个question的vector，所以attention计算得到三组权重，然后求三组权重每个位置上的max，然后进行后面的操作。

模型VQA¹，用了这个思想。

VQA

$$图5$$
注意看这里的question变成表征后有多个vector。图片经过CNN切割成多个小区域，然后也是分两组向量，分别计算权重和求和。

假设question抽取后有T个向量，然后做attention操作得到T组向量（ $C_1...C_T$ ），然后做max操作，然后进行分类计算。

首先概述了所提出的SMemVQA网络，如图5(a)所示。

网络的输入是一个由长度可变的问题序列和大小固定的图像组成的问题。

问题中的每个单词首先被表示为一个one-hot 向量。然后，每个one-hot 向量被嵌入到一个实数词向量中，$V=\left\{v_j\mid v_j\in {\mathbb{R}}^N;j=1,\cdots ,T\right\}$，其中$T$为问题中的最大字数，$N$为嵌入空间的维数。长度小于$T$的句子用特殊的$-1$值填充，嵌入到全零词向量中。

问题中的单词被用来计算视觉记忆的注意力，其中包含提取的图像特征。通过CNN对输入图像进行处理，提取空间位置网格上的高水平 $M$维度视觉特征。具体来说，我们用$S=\{s_i\mid s_i\in$ ${\mathbb{R}}^M;i=1,\cdots ,L\}$ 来表示每个网格位置的空间CNN特征。本文使用GoogLeNet最后一层卷积层的空间特征输出作为图像的视觉特征。

每个位置的图像特征向量与词向量一起嵌入到一个共同的语义空间中。使用了两种不同的嵌入方法:注意嵌入$W_A$和视觉论点嵌入$W_E$。注意嵌入投射每个视觉特征向量，使其与问题词嵌入相结合产生该图像空间的注意权重。视觉论点嵌入检测问题中语义概念或对象的存在，并将嵌入结果与注意权重相乘，对所有位置求和，生成视觉论点向量$S_{att}$。

最后，将视觉论点向量与问题表示相结合，用于预测给定图像和问题的答案。

单跳模型中的词引导空间注意

第一跳的注意结构(图 5b)使用每个词向量分别提取记忆中相关的视觉特征，让每个单词选择一个相关区域可能会提供更细粒度的注意。单词向量$V$和视觉特征$S$之间的关联矩阵$C\in {\mathbb{R}}^{T\times L}$中计算为
$$C=V\cdot {\left(S\cdot W_A+b_A\right)}^T$$
其中$W_A\in {\mathbb{R}}^{MN}$中包含视觉特征$S$的注意嵌入权值， $b_A\in {\mathbb{R}}^{LN}$中是偏项。该关联矩阵是每个单词嵌入和每个空间位置的视觉特征点积的结果，因此关联矩阵$C$中的每个值度量了每个单词和每个空间的视觉特征之间的相似性。

空间注意权值$W_{att}$的计算方法是对相关矩阵$C$取单词维度$T$上的最大值，对每个空间位置选择最高的相关值，然后应用softmax函数
$$W_{att}=\mathrm{softmax}\left(\underset{i=1,\cdots ,T}{\max }\left(C_i\right)\right),C_i\in {\mathbb{R}}^L$$
此时注意力权重 $W_{att}\in {\mathbb{R}}^L$ 对于问题所指的位置是高的，而对于其他地点是低的，权重之和等于1。例如，在图 5中所示的例子中，“篮子里有猫吗?”这个问题为篮子的位置产生了很高的注意力权重，因为篮子的词向量与该位置的视觉特征高度相关。论点嵌入$W_E$投射了视觉特征 $S$，对某些语义概念产生高激活。例如，在图5中，它在包含猫的区域有高激活。然后将论点嵌入的结果乘以生成的注意权重$W_{att}$，求和得到选择的视觉“论点”向量$S_{att}\in {\mathbb{R}}^N$,
$$S_{att}=W_{att}\cdot \left(S\cdot W_E+b_E\right)$$
在图5中，这一步将在篮子位置积累猫的存在特征。

最后，利用该论点向量$S_{att}$ 和问题嵌入$Q$的总和来预测给定图像和问题的答案。对于问题表示$Q$，选择词袋(BOW)。其他问题表示形式，如LSTM，也可以使用，但是，BOW的参数较少，但表现出了良好的性能。
$$Q=W_Q\cdot V+b_Q$$
其中 $W_Q\in {\mathbb{R}}^T$ 表示单词向量 $V$的BOW权重 , $b_Q\in {\mathbb{R}}^N$ 是偏置项。最后的预测$P$是
$$P=\mathrm{softmax}\left(W_P\cdot f\left(S_{att}+Q\right)+b_P\right)$$
其中$W_P\in {\mathbb{R}}^{K\times N}$,$b_P\in {\mathbb{R}}^K$是偏置项。 $K$表示可能的预测答案个数。$f$是激活函数。

在图5中，此步骤将在篮子位置附近为cat收集的论点添加到问题中，并且，由于没有找到猫，因此预测答案为“否”。在预测最终答案之前，注意力和论点计算步骤可以在另一跳中选择性地重复。

两跳模型中的空间注意

利用重复跳来促进更深的推断，在每一跳收集额外的论点。回想一下，将视觉论点向量$S_{att}$添加到第一个跳的问题表示$Q$中，生成一个更新的问题向量。
$$O_{hop1}=S_{att}+Q$$
在下一跳中，使用向量$O_{hop1}\in {\mathbb{R}}^N$中替换单个单词向量$V$，从记忆中提取与整个问题相关的额外视觉特征，并更新视觉论点。

第一跳的相关矩阵$C$从问题中的每个词向量$V$中提供细粒度的局部论点，而下一跳的相关向量$C_{hop2}$从整个问题表示$Q$中考虑全局论点。

相关向量 $C_{\text{hop }2}\in {\mathbb{R}}^L$ ：
$$C_{\text{hop }2}=\left(S\cdot W_E+b_E\right)\cdot O_{\text{hop }1}$$
$W_E\in {\mathbb{R}}^{M\times N}$ 是视觉特征$S$的注意嵌入权重.与第一跳的论点嵌入权值共享.

空间注意权值$W_{att}$
$$W_{att2}=\mathrm{softmax}\left(C_{\text{hop }2}\right)$$
然后，第二跳中相关的视觉信息 $S_{att2}\in {\mathbb{R}}^N$:
$$S_{att2}=W_{att2}\cdot \left(S\cdot W_{E_2}+b_{E_2}\right)$$

---

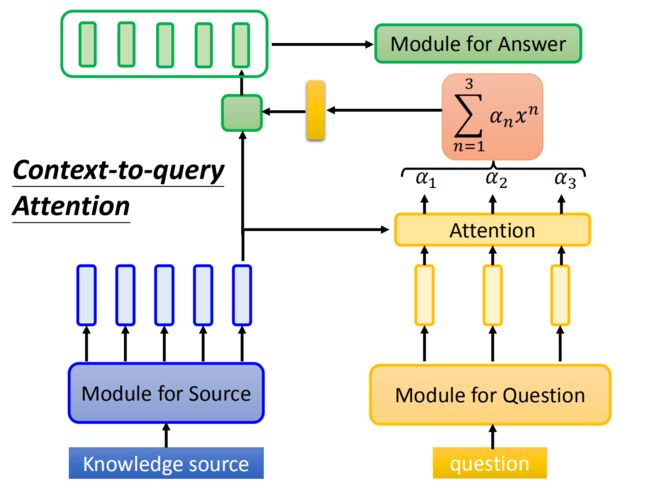
3、文章对问题的注意力 Context-to-query Attention

$$图6$$

当然，这两种方法都是问题去对文章做Attention，其实也可以反过来，用文章对问题做Attention。一样的计算方式，得到相乘累加的结果，如上图的黄色向量，再通过这个向量与文章token的词向量做某种方式的计算，在文献上有两者相加、点乘、拼接等等得到绿色的向量。最终，通过每一个文章的词向量得到的绿色向量序列得到最终的答案，典型的模型有R-Net、Fusion Network。

R-Net

$$图7$$

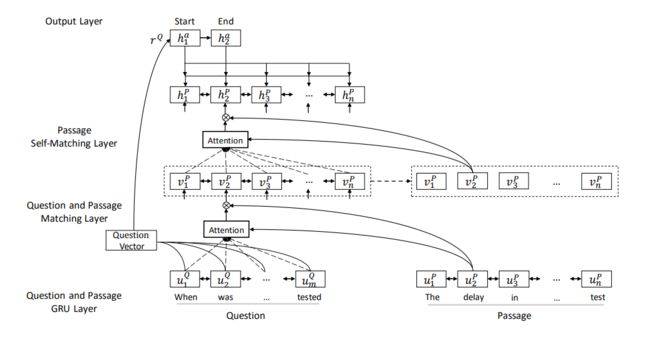
图7给出了网络的结构²。

1. 首先，采用BiRNN网络分别对问题和文章进行处理，得到 $u_1^Q,\dots ,u_m^Q$ 和 $u_1^P,\dots ,u_n^P$，即

$$\begin{array}{rl}{u}_t^Q& ={\mathrm{BiRNN}}_Q\left(u_{t-1}^Q,\left[e_t^Q,c_t^Q\right]\right)\\ u_t^P& ={\mathrm{BiRNN}}_P\left(u_{t-1}^P,\left[e_t^P,c_t^P\right]\right)\end{array}$$

$e_t^Q,c_t^Q$ 分别是词嵌入和字符嵌入。

2. 然后，将问题和文章与基于注意力的门控循环网络进行匹配，得到文章的问题注意力表征${\left\{v_t^P\right\}}_{t=1}^n$。

$$v_t^P=\mathrm{RNN}\left(v_{t-1}^P,\left[u_t^P,c_t\right]\right)$$

$c_t=\mathrm{att}\left(u^Q,\left[u_t^P,v_{t-1}^P\right]\right)$ 是通过对 $\left(u^Q\right)$ 计算的上下文向量:
$$\begin{array}{c}{s}_j^t={\mathrm{v}}^{\mathrm{T}}\tanh \left(W_u^Q{u}_j^Q+W_u^P{u}_t^P+W_v^P{v}_{t-1}^P\right)\\ a_i^t=\exp \left(s_i^t\right)/{\Sigma }_{j=1}^m\exp \left(s_j^t\right)\\ c_t={\Sigma }_{i=1}^m{a}_i^t{u}_i^Q\end{array}$$
每个问题注意力表征$v_t^P$动态地合并了来自整个问题的聚合匹配信息。

为了确定文章那部分的重要性并关注与问题相关的部分，在输入 $\left(\left|u_t^P,c_t\right|\right)$ 中添加了另一个RNN门 :

$$\begin{array}{c}{g}_t=\mathrm{sigmoid}\left(W_g\left[u_t^P,c_t\right]\right)\\ {\left[u_t^P,c_t\right]}^{\ast }=g_t\odot \left[u_t^P,c_t\right]\end{array}$$
${\left[u_t^P,c_t\right]}^{\ast }$ 代替 $\left[u_t^P,c_t\right]$.

3. 在此基础上，将自注意力应用于从整个段落中收集论点并细化段落表示，然后将其输入输出层以预测答案跨度的边界.

它动态地从整个篇章中提取论点，并将与当前篇章词与问题信息相关的论点编码到篇章表征$h_t^P$中
$$h_t^P=\mathrm{BiRNN}\left(h_{t-1}^P,\left[v_t^P,c_t\right]\right)$$
$c_t=\mathrm{att}\left(v^P,v_t^P\right)$ 是通过$\left(v^P\right)$ 计算的上下文向量:
$$\begin{array}{c}{s}_j^t={\mathrm{v}}^{\mathrm{T}}\tanh \left(W_v^P{v}_j^P+W_v^{\tilde{P}}{v}_t^P\right)\\ a_i^t=\exp \left(s_i^t\right)/{\Sigma }_{j=1}^n\exp \left(s_j^t\right)\\ c_t={\Sigma }_{i=1}^n{a}_i^t{v}_i^P\end{array}$$
$\left[v_t^P,c_t\right]$ 也使用上面的门产出 ${\left[u_t^P,c_t\right]}^{\ast }$

使用指针网络预测答案的开始和结束位置。
$$\begin{array}{c}{s}_j^t={\mathrm{v}}^{\mathrm{T}}\tanh \left(W_h^P{h}_j^P+W_{\mathrm{h}}^a{h}_{t-1}^a\right)\\ a_i^t=\exp \left(s_i^t\right)/{\Sigma }_{j=1}^n\exp \left(s_j^t\right)\\ p^t=\arg \max \left(a_1^t,\dots ,a_n^t\right)\end{array}$$
这里$h_{t-1}^a$表示指针网络的最后一个隐藏状态。指针网络的输入是基于当前预测概率$a^t$的上下文向量
$$\begin{array}{c}{c}_t={\Sigma }_{i=1}^n{a}_i^t{h}_i^P\\ h_t^a=\mathrm{RNN}\left(h_{t-1}^a,c_t\right)\end{array}$$
此外，在问题表征上使用上下文向量来生成指针网络的初始隐藏向量。当预测开始位置时 ，$h_{t-1}^a$表示指针网络初始隐藏状态。利用问题向量$r^Q$作为指针网络的初始状态。$r^Q=\mathrm{att}\left(u^Q，V_r^Q\right)$是一个基于参数$V_r^Q$的上下文向量:
$$\begin{array}{c}{s}_j={\mathrm{v}}^{\mathrm{T}}\tanh \left(W_u^Q{u}_j^Q+W_{\mathrm{v}}^Q{V}_r^Q\right)\\ a_i=\exp \left(s_i\right)/{\Sigma }_{j=1}^m\exp \left(s_j\right)\\ r^Q={\Sigma }_{i=1}^m{a}_i{u}_i^Q\end{array}$$
为了训练网络，通过预测的分布来最小化真实起始位置和结束位置的负对数概率之和。

Fusion Network

一种端到端架构:全感知融合网络(FusionNet)³。给定文本A和B, FusionNet将文本$\mathrm{B}$中的信息融合到文本$\mathrm{A}$中，并生成两组向量
$$U_A=\left\{{\mathbf{u}}_1^A,\dots ,{\mathbf{u}}_m^A\right\},U_B=\left\{{\mathbf{u}}_1^B,\dots ,{\mathbf{u}}_n^B\right\}$$
下面，我们考虑文本$\mathrm{A}$是context $\mathbf{C}$，文本$\mathrm{B}$是question $\mathbf{Q}$的特殊情况。FusionNet的插图如图8所示。它由以下组件组成。

$$图8$$

1. 输入向量。

首先，将$C$和$Q$中的每个单词转换为输入向量$\mathbf{w}$。还包括12 -dim POS嵌入，8 -dim NER嵌入，以及上下文$C$的标准化频率。
$$\left\{{\mathbf{w}}_1^C,\dots ,{\mathbf{w}}_m^C\right\}\subset {\mathbb{R}}^{900+20+1}\text{ , and }\left\{{\mathbf{w}}_1^Q,\dots ,{\mathbf{w}}_n^Q\right\}\subset {\mathbb{R}}^{900}$$

2. 全感知多层次的融合:词级

在多级融合中，分别考虑了词级和更高层次的融合。词级融合告知$C$ $Q$中有哪些词。如图8中的箭头(1)所示。首先，为$C$中的每个单词创建一个特征向量${\mathrm{e}\mathrm{m}}_i$，以指示该单词是否出现在问题Q中。其次，使用基于注意的嵌入 ${\mathbf{g}}_i$融合
$${\hat{\mathbf{g}}}_i^C=\sum _j{\alpha }_{ij}{\mathbf{g}}_j^Q,{\alpha }_{ij}\propto \exp \left(S\left({\mathbf{g}}_i^C,{\mathbf{g}}_j^Q\right)\right),S(\mathbf{x},\mathbf{y})=\mathrm{ReLU}(W\mathbf{x}{)}^T\mathrm{ReLU}(W\mathbf{y})$$
$W\in {\mathbb{R}}^{300\times 300}$. 因为单词的历史本身就是输入向量，所以全意识的注意在这里并不适用。上下文的增强输入向量是 ${\tilde{\mathbf{w}}}_i^C=\left[{\mathbf{w}}_i^C;{\mathrm{e}\mathrm{m}}_i;{\hat{\mathbf{g}}}_i^C\right]$.

3. Reading.

   在读取器中，使用一个 BiLSTM来形成$\mathbf{C}$和 $\mathbf{Q}$ 的低级和高级概念为${\mathbf{h}}^l,{\mathbf{h}}^h\in {\mathbb{R}}^{250}$。

$$\begin{array}{rl}{\mathbf{h}}_1^{Cl},\dots ,{\mathbf{h}}_m^{Cl}& =\mathrm{BiLSTM}\left({\tilde{\mathbf{w}}}_1^C,\dots ,{\tilde{\mathbf{w}}}_m^C\right),{\mathbf{h}}_1^{Ql},\dots ,{\mathbf{h}}_n^{Ql}=\mathrm{BiLSTM}\left({\mathbf{w}}_1^Q,\dots ,{\mathbf{w}}_n^Q\right)\\ {\mathbf{h}}_1^{Ch},\dots ,{\mathbf{h}}_m^{Ch}& =\mathrm{BiLSTM}\left({\mathbf{h}}_1^{Cl},\dots ,{\mathbf{h}}_m^{Cl}\right),{\mathbf{h}}_1^{Qh},\dots ,{\mathbf{h}}_n^{Qh}=\mathrm{BiLSTM}\left({\mathbf{h}}_1^{Ql},\dots ,{\mathbf{h}}_n^{Ql}\right)\end{array}$$

4. Question Understanding.

在问题理解中，应用了一个新的BiLSTM，包含了${\mathbf{h}}^{Ql}，{\mathbf{h}}^{Qh}$，以获得最终的问题表征$U_Q$:
$$U_Q=\left\{{\mathbf{u}}_1^Q,\dots ,{\mathbf{u}}_n^Q\right\}=\mathrm{BiLSTM}\left(\left[{\mathbf{h}}_1^{Ql};{\mathbf{h}}_1^{Qh}\right],\dots ,\left[{\mathbf{h}}_n^{Ql};{\mathbf{h}}_n^{Qh}\right]\right)$$
其中${\left\{{\mathbf{u}}_i^Q\in {\mathbb{R}}^{250}\right\}}_{i=1}^n$ 问题 $\mathbf{Q}$.的理解向量。

5. 全感知多层次的融合:高级

   通过对单词历史的充分关注，将问题$Q$中的所有高级信息融合到上下文$C$中。由于全感知注意评分函数被限制为对称的，需要为$\mathbf{C}$和$\mathbf{Q}$确定单词的共同历史

$${\mathrm{H}\mathrm{o}\mathrm{W}}_i^C=\left[{\mathbf{g}}_i^C;{\mathbf{c}}_i^C;{\mathbf{h}}_i^{Cl};{\mathbf{h}}_i^{Ch}\right],{\mathrm{H}\mathrm{o}\mathrm{W}}_i^Q=\left[{\mathbf{g}}_i^Q;{\mathbf{c}}_i^Q;{\mathbf{h}}_i^{Ql};{\mathbf{h}}_i^{Qh}\right]\in {\mathbb{R}}^{1400}$$

其中${\mathbf{g}}_i$是GloVe 嵌入，${\mathbf{c}}_i$是CoVe嵌入。然后，通过全意识的注意力，融合从$Q$到$C$的低、高、和理解层次的信息。通过注意函数$S^l(\mathbf{x},\mathbf{y}),S^h(\mathbf{x},\mathbf{y}),S^u(\mathbf{x},\mathbf{y})$计算不同组的注意权重，将低、高、理解概念结合起来。隐藏大小设置为$k=250$。

• 对词语历史的全感知注意力

  当我们阅读上下文时，每个输入的单词都会逐渐转化为更抽象的表示，例如，从低级到高级的概念。总之，它们构成了我们脑海中每个单词的历史。对于人类来说，我们经常使用单词的历史，但我们往往忽视了它的重要性。

  在神经结构中，将第$i$ 个单词${\mathrm{H}\mathrm{o}\mathrm{W}}_i$的历史定义为该单词生成的所有表示的连接。这可能包括单词嵌入，RNN中的多个中间和输出隐藏向量，以及在任何进一步的层中相应的表示向量。为了将单词的历史整合到广泛的神经模型中，使用全感知注意力。

  使用注意力将信息从一个物体融合到另一个物体上。考虑文本 $\mathrm{A}$和$\mathrm{B}$中的单词的两组隐藏向量:$\left\{{\mathbf{h}}_1^A,\dots ,{\mathbf{h}}_m^A\right\},\left\{{\mathbf{h}}_1^B,\dots ,{\mathbf{h}}_n^B\right\}\subset {\mathbb{R}}^d$。它们的相关历史是，
  $$\left\{{\mathrm{H}\mathrm{o}\mathrm{W}}_1^A,\dots ,{\mathrm{H}\mathrm{o}\mathrm{W}}_m^A\right\},\left\{{\mathrm{H}\mathrm{o}\mathrm{W}}_1^B,\dots ,{\mathrm{H}\mathrm{o}\mathrm{W}}_n^B\right\}\subset {\mathbb{R}}^{d_h}$$
  $d_h\gg d$. 通过对 A中每一个${\mathbf{h}}_i^A$ 使用注意力将B融入到A。

  1. 计算注意力得分 $S_{ij}=S\left({\mathbf{h}}_i^A,{\mathbf{h}}_j^B\right)\in \mathbb{R}$ ， 对于每一个${\mathbf{h}}_j^B$ 在$\mathrm{B}$ 中。
  2. 形成注意力权重 ${\alpha }_{ij}$ : ${\alpha }_{ij}=\exp \left(S_{ij}\right)/{\sum }_k\exp \left(S_{ik}\right)$.
  3. 将${\mathbf{h}}_i^A$与汇总信息连接起来, ${\hat{\mathbf{h}}}_i^A={\sum }_j{\alpha }_{ij}{\mathbf{h}}_j^B$.

  在全感知注意中，用单词的历史来代替注意力分数的计算。
  $$S\left({\mathbf{h}}_i^A,{\mathbf{h}}_j^B\right)⟹S\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^A,{\mathrm{H}\mathrm{o}\mathrm{W}}_j^B\right)$$
  这会完全意识到对每个单词的完全理解。

  为了充分利用注意中的单词历史，需要一个适当的注意评分函数$S(\mathbf{x}，\mathbf{y})$。一个常用的函数是乘法注意
  $$S_{ij}={\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^A\right)}^T{U}^{T}V\left({\mathrm{H}\mathrm{o}\mathrm{W}}_j^B\right)$$
  其中 $U,V\in {\mathbb{R}}^{k\times d_h}$，和$k$是注意力隐藏的大小。然而，怀疑两个大的矩阵直接交互会使神经模型更难训练。因此，约束矩阵$U^{T}V$为对称的，可以分解成$U^{T}DU$，因此
  $$S_{ij}={\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^A\right)}^T{U}^{T}DU\left({\mathrm{H}\mathrm{o}\mathrm{W}}_j^B\right)$$
  其中 $U\in {\mathbb{R}}^{k\times d_h},D\in {\mathbb{R}}^{k\times k}$ 和 $D$是一个对角矩阵。对称形式保留了在不同的${\mathrm{H}\mathrm{o}\mathrm{W}}_i^A，{\mathrm{H}\mathrm{o}\mathrm{W}}_j^B$之间给予高注意力分数的能力。此外，将非线性与对称形式结合在一起，从而在单词历史的不同部分之间提供更丰富的交互。注意力得分的最终公式是
  $$S_{ij}=f{\left(U\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^A\right)\right)}^{T}Df\left(U\left({\mathrm{H}\mathrm{o}\mathrm{W}}_j^B\right)\right)$$
  $f(x)=\max (0,x).$

1. 低级融合: ${\hat{\mathbf{h}}}_i^{Cl}={\sum }_j{\alpha }_{ij}^l{\mathbf{h}}_j^{Ql},{\alpha }_{ij}^l\propto \exp \left(S^l\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^C,{\mathrm{H}\mathrm{o}\mathrm{W}}_j^Q\right)\right)$.
2. 高级融合: ${\hat{\mathbf{h}}}_i^{Ch}={\sum }_j{\alpha }_{ij}^h{\mathbf{h}}_j^{Qh},{\alpha }_{ij}^h\propto \exp \left(S^h\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^C,{\mathrm{H}\mathrm{o}\mathrm{W}}_j^Q\right)\right)$.
3. 理解级融合: ${\hat{\mathbf{u}}}_i^C={\sum }_j{\alpha }_{ij}^u{\mathbf{u}}_j^Q,{\alpha }_{ij}^u\propto \exp \left(S^u\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^C,{\mathrm{H}\mathrm{o}\mathrm{W}}_j^Q\right)\right)$.

这种多层次的注意力机制在考虑所有层次信息的同时，独立捕获不同层次的信息。应用一种新的BiLSTM得到完全融合$Q$中信息的$C$表征:
$$\left\{{\mathbf{v}}_1^C,\dots ,{\mathbf{v}}_m^C\right\}=\mathrm{BiLSTM}\left(\left[{\mathbf{h}}_1^{Cl};{\mathbf{h}}_1^{Ch};{\hat{\mathbf{h}}}_1^{Cl};{\hat{\mathbf{h}}}_1^{Ch};{\hat{\mathbf{u}}}_1^C\right],\dots ,\left[{\mathbf{h}}_m^{Cl};{\mathbf{h}}_m^{Ch};{\hat{\mathbf{h}}}_m^{Cl};{\hat{\mathbf{h}}}_m^{Ch};{\hat{\mathbf{u}}}_m^C\right]\right)$$

6. Fully-Aware Self-Boosted Fusion

现在使用自增强融合来考虑环境中的遥远部分，如图8中的箭头(3)所示。再一次，通过对文字历史的充分关注来实现这一点。确定了单词的历史
$${\mathrm{H}\mathrm{o}\mathrm{W}}_i^C=\left[{\mathbf{g}}_i^C;{\mathbf{c}}_i^C;{\mathbf{h}}_i^{Cl};{\mathbf{h}}_i^{Ch};{\hat{\mathbf{h}}}_i^{\mathrm{C}\mathrm{l}};{\hat{\mathbf{h}}}_i^{\mathrm{C}\mathrm{h}};{\hat{\mathbf{u}}}_i^C;{\mathbf{v}}_i^C\right]\in {\mathbb{R}}^{2400}$$
然后我们进行全意识的注意, ${\hat{\mathbf{v}}}_i^C={\sum }_j{\alpha }_{ij}^s{\mathbf{v}}_j^C,{\alpha }_{ij}^s\propto \exp \left(S^s\left({\mathrm{H}\mathrm{o}\mathrm{W}}_i^C,{\mathrm{H}\mathrm{o}\mathrm{W}}_j^C\right)\right)$.
最终的上下文表示:
$$U_C=\left\{{\mathbf{u}}_1^C,\dots ,{\mathbf{u}}_m^C\right\}=\mathrm{BiLSTM}\left(\left[{\mathbf{v}}_1^C;{\hat{\mathbf{v}}}_1^C\right],\dots ,\left[{\mathbf{v}}_m^C;{\hat{\mathbf{v}}}_m^C\right]\right)$$
${\left\{{\mathbf{u}}_i^C\in {\mathbb{R}}^{250}\right\}}_{i=1}^m$ 是 $\mathbf{C}$.理解向量

在FusionNet的这些组件之后，创建了理解向量$U_C$，用于上下文$C$，它与问题$Q$完全融合。对于$Q$问题，也有向量$U_Q$。

机器理解

SQuAD 的答案总是上下文中的一个跨度。FusionNet的输出是两者的理解向量
$$\mathbf{C}\text{ and }\mathbf{Q},U_C=\left\{{\mathbf{u}}_1^C,\dots ,{\mathbf{u}}_m^C\right\},U_Q=\left\{{\mathbf{u}}_1^Q,\dots ,{\mathbf{u}}_n^Q\right\}$$
然后使用它们来查找上下文中的答案span。首先，通过${\mathbf{u}}^Q={\sum }_i{\beta }_i{\mathbf{u}}_i^Q$，得到单个概括的问题理解向量，其中${\beta }_i\propto \exp \left({\mathbf{w}}^T{\mathbf{u}}_i^Q\right)$和$\mathbf{w}$是可训练向量。然后用总结问题理解向量${\mathbf{u}}^Q$，
$$P_i^S\propto \exp \left({\left({\mathbf{u}}^Q\right)}^T{W}_S{\mathbf{u}}_i^C\right)$$
其中 $W_S\in {\mathbb{R}}^{d\times d}$ 是一个可训练矩阵. 为了在跨度结束时使用跨度开始的信息， 通过GRU将跨度开始的上下文理解向量与${\mathbf{u}}^Q$结合起来
$${\mathbf{v}}^Q=\mathrm{GRU}\left({\mathbf{u}}^Q,\sum _i{P}_i^S{\mathbf{u}}_i^C\right)$$
其中${\mathbf{u}}^Q$ 作为记忆和${\sum }_i{P}_i^S{\mathbf{u}}_i^C$ 作为输入，最后，使用${\mathbf{v}}^Q$得到结束位置
$$P_i^E\propto \exp \left({\left({\mathbf{v}}^Q\right)}^T{W}_E{\mathbf{u}}_i^C\right)$$
在训练过程中，我们最大限度地提高真实跨度的对数概率
$$\sum _k\left(\log \left(P_{i_k^s}^S\right)+\log \left(P_{i_k^e}^E\right)\right)$$
$i_k^s，i_k^e$是$k$ -th实例的答案span。

预测在约束条件$0\le i^e-i^s\le 15$下，答案跨度$i^s,i^e$是最大的$P_{i^s}^S{P}_{i^e}^E$

---

4、双向注意力

既然上面提到question和passage可以相互做attention，于是把这两种方法结合起来就变成了一个新模型，代表模型有BIDAF，DCN,QANET。

BiDAF

双向注意流(BIDAF)⁴网络，这是一个分层的多阶段体系结构(图 9)。BIDAF网络包括字符级、单词级和文章嵌入。并使用双向注意流获得查询感知上下文表征。该注意机制对以前流行的注意进行改进。

• 首先，注意层没有将上下文段落融合成一个固定大小的向量。相反，每个时间步的注意力都被计算出来，并且每个时间步的注意向量，以及来自前一层的表征，都被允许流向后续的建模层。这减少了早期融合造成的信息损失。
• 第二，使用无记忆注意机制。通过时间迭代计算注意，但每个时间步长的注意仅是当前时间步长的查询和上下文段落的函数，并不直接依赖于前一个时间步长的注意。这种简化导致了注意层和建模层之间的劳动分工。它迫使注意层集中于学习查询和文章之间的注意力，并使建模层集中于学习上下文表征(注意层的输出)。它还允许每个时间步骤的注意力不受前一个时间步骤不正确的影响。
• 第三，在查询到文章和文章到查询两个方向上都使用注意机制，相互提供互补的信息。

$$图9$$
图9中，机器理解模型由六层组成

1. Character Embedding Layer

   字符转为随机初始化的向量 ，作为CNN的一维输入，使用最大池化，为每个单词获得一个固定大小的向量，其维度为CNN的输入通道的数目。

2. Word Embedding Layer

   预训练模型提供

字符和单词嵌入向量的连接被传递到双层 Highway Network，输出是两个$d$维矩阵:用于上下文$\mathbf{X}\in {\mathbb{R}}^{d\times T}$和用于查询$\mathbf{Q}\in {\mathbb{R}}^{d\times J}$。

3. Contextual Embedding Layer.

   使用BiLSTM学习单词之间的交互信息。因此，从词向量$\mathbf{X}$中获得$\mathbf{H}\in {\mathbb{R}}^{2d\times T}$，并从查询词向量$\mathbf{Q}$中获得$\mathbf{U}\in {\mathbb{R}}^{2d\times J}$。注意，$\mathbf{H}$和$\mathbf{U}$的每个列向量都是$ 2d $ 维。

值得注意的是，该模型的前三层是不同粒度的查询和文章的计算特征，类似于计算机视觉领域中CNN的多阶段特征计算。

4. Attention Flow Layer.

   该层输入是文章$\mathbf{H}$和查询$\mathbf{U}$的向量表示。该层的输出是文章词的查询感知向量表示$\mathbf{G}$。

   在这一层中，从两个方向计算注意:从文章到查询以及从查询到文章。

   首先计算一个共享相似度矩阵$\mathbf{S}\in {\mathbb{R}}^{T\times J}$。其中${\mathbf{S}}_{tj}$表示第$t$ 个文章词和第$j$ 个查询词之间的相似性。相似度矩阵由
   $${\mathbf{S}}_{tj}=\alpha \left({\mathbf{H}}_{:t},{\mathbf{U}}_{:j}\right)\in \mathbb{R}$$
   $\alpha$ 是可训练的标量函数，${\mathbf{H}}_{:t}$是$\mathbf{H}$的第$t$ 列向量，${\mathbf{U}}_{:j}$是$\mathbf{U}$的第$j$ 列向量，其中
   $$\alpha (\mathbf{h},\mathbf{u})={\mathbf{w}}_{(\mathbf{S})}^{\top }[\mathbf{h};\mathbf{u};\mathbf{h}\odot \mathbf{u}]$$

   ${\mathbf{w}}_{(\mathbf{S})}\in {\mathbb{R}}^{6d}$ 是参数， $\odot$ 意味着元素乘法。 $[;]$ 跨行向量串联。现在使用$\mathbf{S}$来获得两个方向上的注意和注意上下文向量。

   • Context-to-query Attention. 图9中绿色模块

     C2Q 对于文章词，计算查询词的权重 ，即查询词重要程度的加权和。让${\mathbf{a}}_t\in {\mathbb{R}}^J$ 表示查询词上 对第 $t$ 个文章词的注意权值，
     $${\mathbf{a}}_t=\mathrm{softmax}\left({\mathbf{S}}_{t:}\right)\in {\mathbb{R}}^J$$
     然后每个参与的查询向量是${\tilde{\mathbf{U}}}_{:t}={\sum }_j{\mathbf{a}}_{tj}{\mathbf{U}}_{:j}.$因此$\tilde{\mathbf{U}}$是包含整个文章参与的$ 2d $ 查询向量。

   • Query-to-context Attention. 图9中橙色模块

     Q2C 注意表示与查询相关的文章中最重要单词的加权和，因此对回答查询至关重要。

     获得对文章词的注意权重
     $$\mathbf{b}=\mathrm{softmax}\left(\underset{col}{\max }(\mathbf{S})\right)\in {\mathbb{R}}^T$$
     其中最大函数$\left({\max }_{col}\right)$跨列执行。那么注意上下文向量为
     $$\tilde{\mathbf{h}}=\sum _t{\mathbf{b}}_t{\mathbf{H}}_{:t}\in {\mathbb{R}}^{2d}$$
     $$\tilde{\mathrm{h}}$$在列中平铺$T$次，从而给出$\tilde{\mathbf{H}}\in {\mathbb{R}}^{2d\times T}$。

     最后，将文章嵌入和上下文向量组合在一起生成$\mathbf{G}$，其中每个列向量可以被认为是每个文章词的查询感知表征。定义了$\mathbf{G}$
     $${\mathbf{G}}_{:t}=\mathbf{\beta }\left({\mathbf{H}}_{:t},{\tilde{\mathbf{U}}}_{:t},{\tilde{\mathbf{H}}}_{:t}\right)\in {\mathbb{R}}^{d_{\mathbf{G}}}$$
     $\mathbf{\beta }$是一个可训练的向量函数，它融合了它的(三个)输入向量，$d_{\mathbf{G}}$是$\mathbf{\beta }$函数的输出维数$\text{ (i.e., }{d}_{\mathbf{G}}=8d\text{ ). }$ 。虽然$\mathbf{\beta }$函数可以是任意可训练的神经网络，如多层感知器，也可以是
     $$\mathbf{\beta }(\mathbf{h},\tilde{\mathbf{u}},\tilde{\mathbf{h}})=[\mathbf{h};\tilde{\mathbf{u}};\mathbf{h}\circ \tilde{\mathbf{u}}]$$

5. Modeling Layer.

   建模层的输入是$\mathbf{G}$，它对文章单词的查询感知表示进行了编码。建模层的输出捕获以查询为条件的文章词之间的交互。

   使用两层双向LSTM，每个方向的输出大小为$d$。因此，得到了一个矩阵$\mathbf{M}\in {\mathbb{R}}^{2d\times T}$中，它被传递到输出层来预测答案。$\mathbf{M}$的每个列向量期望包含关于单词的关于整个文章段落和查询的上下文信息。

6. Output Layer.

   输出层是特定于任务的。这里，描述QA任务的输出层。

   QA任务要求模型找到段落的子短语来回答查询。这个短语是通过预测该短语在段落中的开始和结束索引而衍生出来的。计算开始索引在整个段落的概率分布
   $${\mathbf{p}}^1=\mathrm{softmax}\left({\mathbf{w}}_{\left({\mathbf{p}}^1\right)}^{\top }[\mathbf{G};\mathbf{M}]\right)$$
   其中${\mathbf{w}}_{\left({\mathbf{p}}^1\right)}\in {\mathbb{R}}^{10d}$中是一个可训练权向量。对于答案短语的结束索引，将$\mathbf{M}$传递到另一个双向LSTM层，并获得${\mathbf{M}}^2\in {\mathbb{R}}^{2d\times T}$。然后，使用${\mathbf{M}}^2$以类似的方式获得结束索引的概率分布:
   $${\mathbf{p}}^2=\mathrm{softmax}\left({\mathbf{w}}_{\left({\mathbf{p}}^2\right)}^{\top }\left[\mathbf{G};{\mathbf{M}}^2\right]\right)$$

   • Training.

   将训练损失(最小化)定义为真实开始和结束指数的负对数概率和预测分布，在所有的例子中平均:
   $$L(\theta )=-\frac{1}{N}\sum _i^N\log \left({\mathbf{p}}_{y_i^1}^1\right)+\log \left({\mathbf{p}}_{y_i^2}^2\right)$$
   $\theta$ 是模型中所有可训练权值的集合，$N$是数据集中的示例数，$y_i^1$和$y_i^2$分别是第$i$ 个示例的真正起始索引和结束索引，${\mathbf{p}}_k$表示向量$\mathbf{p}$的第$k$ 个值。

   • Test.

   答案跨度$(k,l)$，其中$k\le l$的最大值为${\mathbf{p}}_k^1{\mathbf{p}}_l^2$，可以用动态规划在线性时间内计算。

DCN

DCN⁵是动态共同注意网络

图 10展示了DCN的结构。我们首先描述了文档和问题的编码器，然后是共同注意机制和产生答案跨度的动态解码器。

$$图10$$

1. 文档和问题的编码器

   $\left(x_1^Q,x_2^Q,\dots ,x_n^Q\right)$ 为问题单词序列， $\left(x_1^D,x_2^D,\dots ,x_m^D\right)$ 为文档单词序列。使用LSTM编码：
   $$\begin{gathered} d_t={\mathrm{LSTM}}_{\text{enc }}\left(d_{t-1},x_t^D\right) \\ {q}_t={\mathrm{LSTM}}_{\text{enc }}\left(q_{t-1},x_t^Q\right). \end{gathered}$$
   得到文档编码矩阵$D=\left[d_1\dots d_m{d}_{\varnothing }\right]\in {\mathbb{R}}^{\ell \times (m+1)}$，还添加了一个哨兵向量$d_{\varnothing }$，它允许模型不关注输入中的任何特定单词。

   得到问题编码矩阵$Q^{\prime }=\left[\begin{array}{lllc}{q}_1& \dots & q_n& q_{\varnothing }\end{array}\right]\in {\mathbb{R}}^{\ell \times (n+1)}$，还添加了一个哨兵向量$q_{\varnothing }$.为了使得问题编码空间和文档编码空间之间不一样，在问题编码之上引入一个非线性投影层。
   $$Q=\tanh \left(W^{(Q)}{Q}^{\prime }+b^{(Q)}\right)\in {\mathbb{R}}^{\ell \times (n+1)}$$

2. 共同注意机制

   

$$图11$$
一种同时关注问题和文档的共同注意机制，并最终融合两种注意语境。图11提供了共同注意机制的说明。

首先计算相似度矩阵，其中包含所有文档词对和问题词对的相似度得分:
$$L=D^{\top }Q\in {\mathbb{R}}^{(m+1)\times (n+1)}$$
相似度矩阵按行标准化，为问题中的每个单词在整个文档中产生$A^Q$的注意权重；按列标准化，为文档中的每个单词在问题中产生$A^D$的注意权重:
$$\begin{gathered} A^Q=\mathrm{softmax}(L)\in {\mathbb{R}}^{(m+1)\times (n+1)} \\ {A}^D=\mathrm{softmax}\left(L^{\top }\right)\in {\mathbb{R}}^{(n+1)\times (m+1)} \end{gathered}$$
接下来，根据问题的每个单词计算文档的总结或注意上下文向量。
$$C^Q=D{A}^Q\in {\mathbb{R}}^{\ell \times (n+1)}$$
类似地， 根据文档中的每个单词计算问题的总结$Q{A}^D$。

根据文档的每个单词计算前一个注意上下文的总结$C^Q{A}^D$。这两种操作可以并行进行，如下式所示。对$C^Q{A}^D$运算的一种可能的解释是将问题编码映射到文档编码空间。
$$C^D=\left[Q;C^Q\right]A^D\in {\mathbb{R}}^{2\ell \times (m+1)}$$
定义$C^D$，一个问题和文档的相互依赖的表征，作为共同注意上下文。使用符号$[a;b]$用于水平连接向量$a$和$b$。

最后一步是通过双向LSTM将时间序列信息融合到共同注意语境中:
$$u_t=\mathrm{B}\mathrm{i}\mathrm{LSTM}\left(u_{t-1},u_{t+1},\left[d_t;c_t^D\right]\right)\in {\mathbb{R}}^{2\ell }$$
定义 $U=\left[u_1,\dots ,u_m\right]\in {\mathbb{R}}^{2\ell \times m}$，这为选择哪个区间可能是最好的答案提供了基础，作为共同注意编码。

3. 动态指针解码器

   由于SQuAD的性质，生成答案跨度的方法是通过预测跨度的起点和终点。但是，给定一个问题-文档对，文档中可能存在几个直观的答案区间，每个区间对应一个局部最大值。使用一种迭代技术，通过预测起点和预测终点来交替选择一个答案跨度。这种迭代过程允许模型从初始的局部极大值中恢复到对应于不正确的答案区间。

   
   $$图12$$

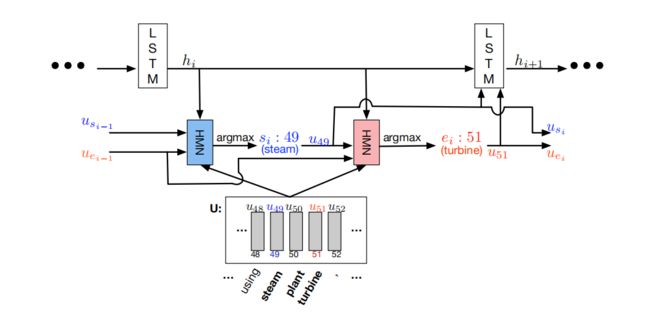
   图12展示了Dynamic Decoder，其状态由lstm产生。在每次迭代中，解码器根据与当前起始和结束位置估计相对应的共同注意编码更新其状态，并通过多层神经网络产生新的起始和结束位置。

   设$h_i，s_i$和$e_i$分别表示LSTM的隐藏状态、起始位置估计和第$i$步 结束位置的估计。LSTM状态更新：
   $$h_i={\mathrm{LSTM}}_{dec}\left(h_{i-1},\left[u_{s_{i-1}};u_{e_{i-1}}\right]\right)$$
   其中$u_{s_i-1}$和$u_{e_{i-1}}$是先前共同注意编码$U$的起始和结束位置的估计。

   已知当前隐藏状态$h_i$、之前的起始位置$u_{s_{i-1}}$和之前的结束位置$u_{e_{i-1}}$，估计当前的起始位置和结束位置。
   $$\begin{array}{l}{s}_i=\underset{t}{\mathrm{argmax}}\left({\alpha }_1,\dots ,{\alpha }_m\right)\\ e_i=\underset{t}{\mathrm{argmax}}\left({\beta }_1,\dots ,{\beta }_m\right)\end{array}$$
   其中${\alpha }_t$和${\beta }_t$表示文档中第$t$个单词对应的开始分数和结束分数。 用单独的神经网络计算${\alpha }_t$和${\beta }_t$。这些网络具有相同的架构，但不共享参数。

   使用 Highway Maxout Network (HMN)来计算${\alpha }_t$，使用这种模型背后的直觉是，QA任务由多种问题类型和文档主题组成。这些变化可能需要不同的模型来估计答案的跨度。Maxout提供了一种跨多个模型集中使用的方法。
   $${\alpha }_t={\mathrm{H}\mathrm{M}\mathrm{N}}_{\text{start }}\left(u_t,h_i,u_{s_{i-1}},u_{e_{i-1}}\right)$$
   这里，$u_t$是对应于文档中$t$ th单词的共同注意编码。HMN ${}_{\text{start}}$如图13所示。结束分数${\beta }_t$的计算方法类似于开始分数${\alpha }_t$，但是使用单独的HMN ${}_{\text{end}}$。

$$图13$$

HMN 计算：
$$\begin{array}{rl}\mathrm{HMN}\left(u_t,h_i,u_{s_{i-1}},u_{e_{i-1}}\right)& =\max \left(W^{(3)}\left[m_t^{(1)};m_t^{(2)}\right]+b^{(3)}\right)\\ r& =\tanh \left(W^{(D)}\left[h_i;u_{s_{i-1}};u_{e_{i-1}}\right]\right)\\ m_t^{(1)}& =\max \left(W^{(1)}\left[u_t;r\right]+b^{(1)}\right)\\ m_t^{(2)}& =\max \left(W^{(2)}{m}_t^{(1)}+b^{(2)}\right)\end{array}$$
$r\in r^{\ell }$是带参数$W^{(D)}\in {\mathbb{R}}^{\ell \times 5\ell }$的当前状态的非线性投影， $m_t^{(1)}$ 是第一个maxout 输出层的输出，$m_t^{(2)}$ 是第二个maxout 输出层的输出，$m_t^{(1)}$ ， $m_t^{(2)}$

喂给最终maxout 输出层，其参数$W^{(3)}\in {\mathbb{R}}^{p\times 1\times 2\ell }$, $b^{(3)}\in {\mathbb{R}}^p$ 。 P是每个maxout层的池化大小。max运算计算张量的第一个维度上的最大值。图13,在第一个最大输出层和最后一个最大输出层之间有高速连接。

4. 为了训练该网络，将所有迭代的起始点和结束点的累积softmax交叉熵最小化。当对起始位置的估计和对结束位置的估计都不再改变时，或者当达到最大迭代次数时，迭代过程停止。

---

QANET

模型包含五个主要组件⁶:一个嵌入层，一个嵌入编码器层，一个文章查询关注层，一个模型编码器层和一个输出层，如图 14所示。

与其他方法的主要区别如下:对于嵌入和编码器，只使用卷积和自注意机制，抛弃了大多数现有的rnn。

因此，模型要快得多，因为它可以并行处理输入标记。注意，卷积和自注意的组合，明显优于单独的自注意，会带来$F1$增益

卷积的使用还允许利用卷积网络中常见的正则化方法，如dropout。

$$图14$$

1. Input Embedding Layer.

   将每个词$w$的词嵌入和字符嵌入连接起来，得到每个词$w$的嵌入$x_w$。词嵌入在训练过程中是固定的，从$p_1=300$ GloVe 预训练初始化。所有词汇表外的单词都被映射到< UNK >令牌。

   每个字符表示为维数$p_2=200$的可训练向量,

   每个单词的长度要么被截断，要么被填充到$16.$取矩阵每一行的最大值来得到每个单词的固定大小的向量表示。

   最后，这一层的给定单词$x$的输出是连接$\left[x_w;x_c\right]\in {\mathbf{R}}^{p_1+p_2}$.其中$x_w$和$x_c$分别是$x$的字符嵌入的卷积输出和单词嵌入的卷积输出。

   采用了highway network。

2. Embedding Encoder Layer.

   编码器层由以下基本构造块组成:

   卷积层 $\times \#+$ self-attention 层+ 前馈层。如图14右上角所示

   使用深度可分离卷积而不是传统的卷积，因为它的记忆效率更高，泛化效果更好。卷积核大小为7,数量$d=128$，如图14右边 block内的conv层数为4。

   self-attention-layer,采用多头注意力机制： Transformer意境级讲解_炫云云

   这些基本操作(conv/self-attention/ffn)都被放置在一个剩余块中，如图1右下方所示。

   对于一个输入$x$和一个给定的操作$f$，输出为$f($ layernorm $(x))+x$，表示每个块从输入到输出有一个完整的标识路径，其中layernorm表示层归一化。

   需要注意的是，这一层的输入是一个维度为$p_1+p_2=500$的向量，对于每个单词，这个向量通过一维卷积立即映射到$d=128$。这一层的输出也是一个维度$d=128$。

3. Context-Query Attention Layer.

   使用$C$和$Q$来表示已编码的文章和查询。

   首先计算文章与查询词之间的相似度，得到一个相似度矩阵$S\in {\mathbf{R}}^{n\times m}$。

   然后通过应用softmax函数对$S$的每一行进行归一化，得到一个矩阵$\bar{S}$。然后文章到查询注意值被计算为$A=\bar{S}\cdot Q^T\in {\mathbf{R}}^{n\times d}$。此处使用的相似函数为三线性函数：
   $$f(q,c)=W_0[q,c,q\odot c]$$
   还使用查询到文章注意，通过softmax函数计算$S$的列归一化矩阵$\overline{\bar{S}}$，查询到文章的注意值为
   $$B=\bar{S}\cdot$$