集成学习(提升方法)
集成方法和提升学习其实都差不多,集成学习(Ensemble Learning)有时被笼统地称作提升(Boosting)方法,广泛用于分类和回归任务。
集成方法思想:使用一些不同的方法改变原始训练样本的分布,从而构建多个不同的分类器,并将这些分类器线性组合得到一个更强大的分类器,来做最后的决策。这不是简单的人多力量大,而是三个臭皮匠赛过诸葛亮,因为这样做往往能产生1+1>2的效果 。
对于集成学习,我们面临两个主要问题:
1.如何改变数据的分布或权重
2.如何将多个弱分类器组合成一个强分类器
针对上述问题,目前主流方法有三种:
1.Boosting方法:包括Adaboosting,提升树(代表是GBDT), XGBoost等
2.Bagging方法:典型的是随机森林
3.Stacking算法
这里简单介绍一下,提升树,Boosting和AdaBoost,RF随机森林。
Boosting和AdaBoost:
在机器学习领域,Boosting算法是一种通用的学习算法,这一算法可以提升任意给定的学习算法的性能。其思想源于1984年Valiant提出的”可能近似正确”-PAC(Probably Approximately Correct)学习模型,在PAC模型中定义了两个概念-强学习算法和弱学习算法。其概念是: 如果一个学习算法通过学习一组样本,识别率很高,则称其为强学习算法;如果识别率仅比随机猜测略高,其猜测准确率大于50,则称其为弱学习算法。
boost模型发展:
1989年Kearns and Valiant研究了PAC学习模型中弱学习算法和强学习算法两者间的等价问题;
即任意给定仅仅比随机猜测稍好(准确率大于0.5)的弱学习算法,是否可以被提升为强学习算法?若两者等价,则我们只需寻找一个比随机猜测稍好的若学习算法,然后将其提升为强学习算法,从而不必费很大力气去直接寻找强学习算法。
就此问题,Schapire于1990年首次给出了肯定的答案。他主持这样一个观点:
任一弱学习算法可以通过加强提升到一个任意正确率的强学习算法,并通过构造一种多项式级的算法来实现这一加强过程,这就是最初的Boosting算法的原型。
Boosting是一种将弱分类器通过某种方式结合起来得到一个分类性能大大提高的强分类器的分类方法。该方法可以把一些粗略的经验规则转变为高度准确的预测法则。强分类器对数据进行分类,是通过弱分类器的多数投票机制进行的。该算法是一个简单的弱分类算法提升过程,这个过程通过不断的训练,以提高对数据的分类能力。
Freund于1991年提出了另外一种效率更高的Boosting算法。但此算法需要要提前知道弱学习算法正确率的下限,因而应用范围十分有限。
adaboost的诞生:
1995年,Freund and Schapire改进了Boosting算法,取名为Adaboost算法,该算法不需要提前知道所有关于弱学习算法的先验知识,同时运算效率与Freund在1991年提出的Boosting算法几乎相同。Adaboost即Adaptive Boosting,它能
1):自适应的调整弱学习算法的错误率,经过若干次迭代后错误率能达到预期的效果。
2):它不需要精确知道样本空间分布,在每次弱学习后调整样本空间分布,更新所有训练样本的权重,把样本空间中被正确分类的样本权重降低,被错误分类的样本权重将会提高,这样下次弱学习时就更能更关注这些被错误分类的样本。该算法可以很容易地应用到实际问题中,因此,已成为目前最流行的Boosting算法。
AdaBoost算法的核心思想是针对同一个训练集训练出不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成一个性能更加强大的分类器(强分类器)。
AdaBoost算法的具体描述如下:
假定X表示样本空间,Y表示样本类别标识集合,假设是二值分类问题,这里限定Y={-1,+1}。令S={(Xi,yi)|i=1,2,…,m}为样本训练集,其中Xi∈X,yi∈Y。
①:始化m个样本的权值,假设样本分布Dt为均匀分布:Dt(i)=1/m,Dt(i)表示在第t轮迭代中赋给样本(xi,yi)的权值。
②:令T表示迭代的次数。


最后,我们可以总结下adaboost算法的一些实际可以使用的场景:
1)用于二分类或多分类的应用场景
2)用于做分类任务的baseline
无脑化,简单,不会overfitting,不用调分类器
3)用于特征选择(feature selection)
4)Boosting框架用于对badcase的修正
只需要增加新的分类器,不需要变动原有分类器
由于adaboost算法是一种实现简单,应用也很简单的算法。Adaboost算法通过组合弱分类器而得到强分类器,同时具有分类错误率上界随着训练增加而稳定下降,不会过拟合等的性质,应该说是一种很适合于在各种分类场景下应用的算法。
提升树:
当boosting算法中的基学习器是决策树时,这个模型算法就叫做提升树。
提升树: 采用boosting算法,优化方法采用前向分步算法,基学习器采用决策树。提升树模型整体结构如下:

进一步展开,具体步骤伪代码如下:

步骤(a)(b)体现了这一点。基分类器是回归树,强依赖关系是:每一颗回归树拟合的是样本在前一棵回归树的残差(当损失函数是平方误差损失时)。有一个问题:当提升树的损失函数为均方误差、指数损失时,每一步优化(最小化损失函数)是简单的(后一棵树拟合前一棵树的残差),但对于一般损失函数而言,往往每一步的优化并不容易。
随机森林:
在随机森林中,集合中的每棵树都是 从训练集中抽取的替换样本中构建的。大量的这样的树,即构成了所说的“森林”。在树的构造过程中分割每个节点时,可以从所有输入特征中找到最佳分割,也可以在1~max_features 范围中随机选取若干个特征进行分割节点操作。
作用:
这两种随机性来源的目的是降低森林估计器的方差。事实上,单个决策树通常表现出高方差,并且倾向于过度拟合。森林中的注入随机性使得决策树具有一定程度的解耦预测误差。
通过取这些预测的平均值,一些错误可以抵消。随机森林通过组合不同的树来减少方差,有时以稍微增加偏差为代价。在实践中,方差的减少通常是显著的,因此产生了一个整体上更好的模型。
对于很多种数据,它可以产生高准确度的分类器;
它可以处理大量的输入变数;
它可以在决定类别时,评估变数的重要性;
在建造森林时,它可以在内部对于一般化后的误差产生不偏差的估计;
它包含一个好方法可以估计遗失的资料,并且,如果有很大一部分的资料遗失,仍可以维持准确度;
这里分享下 sklearn官网的例子 。
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import plot_roc_curve
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
# 使用官网自带的函数,y是类别,y 取值范围为 {1,2,3}
X, y = load_wine(return_X_y=True)
# 将多分类问题转换为二分类问题
y = y == 2
# 分割为训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 训练svc模型
svc = SVC(random_state=42)
svc.fit(X_train, y_train)
输出内容为:
SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
max_iter=-1, probability=False, random_state=42, shrinking=True, tol=0.001,
verbose=False)
# 随机森林分类器
rfc = RandomForestClassifier(n_estimators=10, random_state=42)
# 拟合
rfc.fit(X_train, y_train)
ax = plt.gca()
rfc_disp = plot_roc_curve(rfc, X_test, y_test, ax=ax, alpha=0.8)
svc_disp.plot(ax=ax, alpha=0.8)
plt.show()
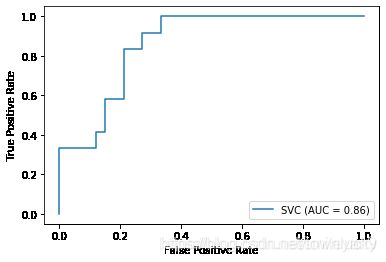
可以看到RandomForests与SVC的ROC曲线图如下:
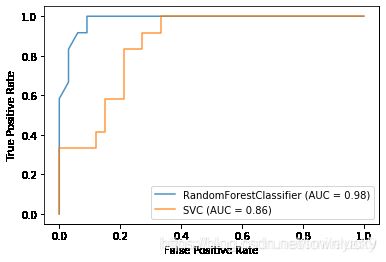
svc模型参数中c默认为1实在太小,而随机森林却把参数n_estimators=10,看起来的确有些不公平,不妨调整一下。可以发现n_estimators=3时效果最佳,AUC=0.99,而SVC中的C=300时才能达到0.96的AUC。
以上就是提升树,Boosting和AdaBoost,RF随机森林的简单介绍。
文章参考:
https://blog.csdn.net/smileyan9/article/details/104545385
https://blog.csdn.net/lanyuelvyun/article/details/88736692