后缀数组的基本定义

子串: 字符串s的子串r[i..j],i<=j,表示r串中从 i 到 j 这一段。

后缀: 后缀是从某个位置 i 开始到整个串末尾结束的一个特殊子串。

        也就是说suffix(i)=r[i..len(s)];

后缀数组：后缀数组sa是一个一维数组，它保存的是1..n的某个排列.

　　　　　sa[1],sa[2],..,sa[n],并保证suffix(sa[i]) < suffix(sa[i+1])

              也就是将s的n个后缀从小到在进行排序之后把排好序的后缀

              的开头位置顺序放入sa中。

名次数组：名次数组rank[i]保存的是suffix(i)在所有后缀中从小到大排列的名次。

 

后缀数组是排列第几是谁。

名次数组是你排第几。

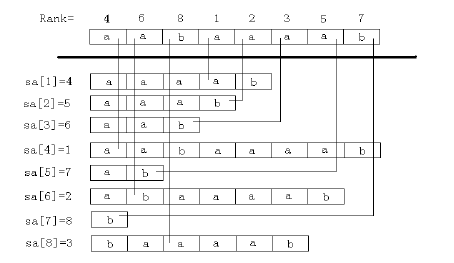
如果还是不清楚，就看看我个人的所思所得吧，绝对原创。

名次                          1      2      3       4       5       6       7      8
排序后的后缀su顺序为 su[4] su[5] su[6] su[1] su[7] su[2] su[8] su[3]
                            aaaab aaab   aab   ……
                              ||
                              \/
                   第4个后缀排在第一位
故：
排序后的名次ra顺序为 ra[4] ra[5] ra[6] ra[1] ra[7] ra[2] ra[8] ra[3]
                             ||     ||     ||     ||    ||     ||    ||     ||
                             1      2       3      4     5     6     7    8

故：
后缀数组sa为：       sa[1] sa[2] sa[3] sa[4] sa[5] sa[6] sa[7] sa[8]
                             ||     ||     ||     ||    ||     ||     ||    ||
                             4      5      6      1     7     2      8     3

很明显的看到：ra[x]=y; sa[y]=x; 相反啊！

常用的数组组合：

su[sa[i]]就表示排序为第 i 的后缀，也就是说su[sa[1]]就是排在第一的后缀。

 

用倍增的方法求rank[i]的具体过程为：

View Code

 

待排序的字符串放在r 数组中，从r[0]到r[n-1]，长度为n，且最大值小于m。

 

为了函数操作的方便，约定除r[n-1]外所有的r[i]都大于0, r[n-1]=0。
函数结束后，结果放在sa 数组中，从sa[0]到sa[n-1]。

 

 

 

下面介绍一个非常有用的数组height[]数组：

height[i]=su[sa[i-1]] 和 su[sa[i]]的最长公共前缀。

                      aaaab…………………… su[1]

height[2]=3      aaab………………………su[2]    

height[3]=2      aab…………………………su[3]

height[4]=3      aabaaaab……………… su[4]

height[5]=1      ab……………………………su[5]

height[6]=2      abaaaab………………… su[6]

height[7]=0      b………………………………su[7]

height[8]=1      baaaab……………………su[8]

这个height[]数组有什么用呢？

对于su[j]和su[k]，不妨设rank[j]<rank[k],（这个不妨是个重点）

那么su[j]和su[k]的最长公共前缀为

min(height[ra[j]+1], height[ra[j]+2]……height[ra[k]]);

所以，su[1]和su[5]的最长公共前缀为

可以看到ra[1]=5 ra[5]=2；

min(height[2+1],height[2+2], height[2+3]) = min(2, 3, 1) = 1;      

再来看一个例子吧。

su[2]和su[6]的最长公共前缀为

可以看到ra[2]=6 ra[6]=3  

min(height[3+1], height[3+2], height[3+3])=min(3, 1, 2)=1;

用o(n)的方法计算出height[n]的代码如下： 

View Code

int rank[maxn], height[maxn];

void calheight(int *r, int *sa, int n)

{

    int i, j, k=0;

    for(i=1; i<=n; i++) rank[sa[i]]=i;

    for(i=0; i<n; height[rank[i++]]=k)

    for(k?k--;0, j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++);

    return;

}