数字图像处理第三章＜一＞、灰度变换
第三章 灰度变换和空间滤波
本章主要介绍图像增强空间域处理的基本知识
一、背景知识
空间域处理基本表达式： g ( x , y ) = T [ f ( x , y ) ] g(x,y) = T[f(x,y)] g(x,y)=T[f(x,y)] 其中：
f(x,y)：输入图像
g(x,y)：输出图像
T：点（x,y）的一个邻域上定义的一个算子
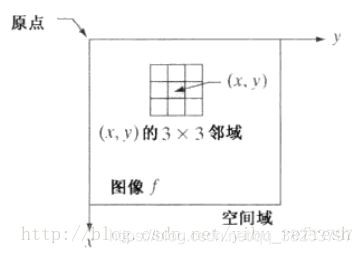
对于任何指定的位置（x,y),输出图像g在这些坐标处的值等于将T应用到f中原点为（x,y)的邻域的结果。
上面的公式也可以写成更一般的形式： S = T ( r ） S = T(r） S=T(r）
s 、 r ：分别表示输出图像和源图像
操作T ：灰度变换函数，可以是对邻域的操作
如果结果只涉及一个点的处理方法叫点处理技术，涉及领域点的叫做邻域处理技术。
二、 灰度变换
2.1、图像反转
对于灰度级别为[0,L-1]的图像，其反转图像： s = L − 1 − r s = L-1-r s=L−1−r
图像反转特别适用于增强嵌入图像暗色区域中的白色或灰色细节，特别是当黑色面积在尺寸上占主导地位时。
2.2、对数变换
对数变换通用形式： s = c l o g ( 1 + r ) , r ≥ 0 , c = c o n s t s = clog(1+r), r≥0, c=const s=clog(1+r),r≥0,c=const
将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值；或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。(扩展暗像素，压缩亮像素)。
反对数变换： 与对数变换相反。
对数变换可用于傅里叶频谱的校正（傅里叶频谱输出值很大级别)会丢失灰度值小的像素信息（因为只用8bit存储），但取对数后可以压缩为个位数防止信息丢失过多）
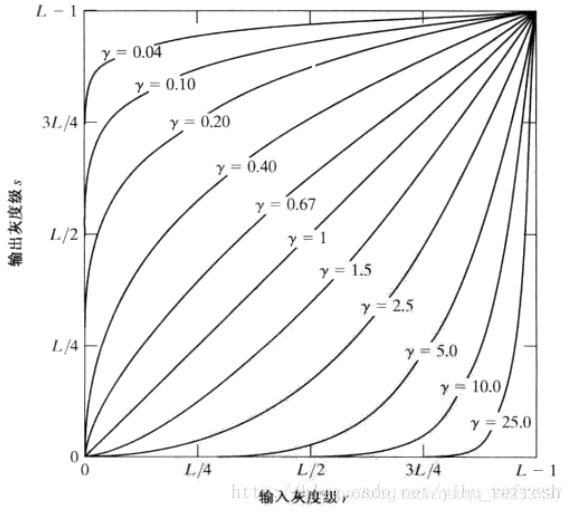
2.3、幂律（伽马）变换
幂律（伽马）变换形式： s = c r y , c = + c o n s t , y = + c o n s t s = cr^y,c=+const,y=+const s=cry,c=+const,y=+const
- γ > 1 γ>1 γ>1和 γ < 1 γ < 1 γ<1时的效果完全相反 c= γ γ γ=1时变换形式变为恒等变换
- 用于伽马矫正，压缩一些灰度范围，扩展一些灰度范围
- 可以增强对比度
- γ > 1 γ>1 γ>1时增强暗部，减少亮部 γ < 1 γ<1 γ<1时增强亮部，减少暗部； γ γ γ越小越亮， γ γ γ越大越暗
- 伽马校正：使用 s = r ( 0.4 ) s=r^(0.4) s=r(0.4) 来预处理图像，产生外观上接近原图像的输出图像
γ > 1 γ>1 γ>1不同值时r和s的关系曲线
2.4、分段线性变换
图像对比度：指的是 一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量，即指一幅图像灰度反差的大小。差异范围越大代表对比越大，差异范围越小代表对比越小，好的对比率120:1就可容易地显示生动、丰富的色彩，当对比率高达300:1时，便可支持各阶的颜色。
优点：形式可以任意复杂
缺点：要求用户输入很多参数
2.4.1、对比度拉伸
2.4.2、灰度级分层
有时需要突出图像中的特定灰度区域，主要有两种方法实现：
- 将感兴趣的范围内的所有灰度值显示为一个值（如白色），再将其他灰度值显示为另外一个值（如黑色）如下左图；
- 将感兴趣的范围内的所有灰度值变亮（或变暗），其他的灰度值不变 如下右图
2.4.3、比特平面分层
像素值是由比特组成的整数。和之前突出灰度级范围不同的是，我们也可以突出特定比特对整个图像外观的贡献。按照图像像素字节的高低位分层图像，如下图所示：
实例：
而这种分解对图像压缩也是有用的。
结论：存储4个最高有效比特平面，就能以可接受的细节和色调重建原图像；而存储这四个图像只是存储原图像的50%。
三、直方图处理
直方图
直方图表示数字图像中每一灰度级像素出现的频次。
直方图反映了图像的清晰程度。直方图均匀分布时，图像最清晰。
令 r k , k = 0 , 1 , 2... , L − 1 r_k,k=0,1,2...,L-1 rk,k=0,1,2...,L−1表示一幅L级灰度数字图像 f ( x , y ) f(x,y) f(x,y)的灰度。 f f f的非归一化直方图定义为： h ( r k ) = n k , k = 0 , 1 , 2.. , L − 1 h(r_k)=n_k,k=0,1,2..,L-1 h(rk)=nk,k=0,1,2..,L−1
其中 n k n_k nk是 f f f中灰度为 r k r_k rk的像素的数量。
对一幅灰度图像，其直方图反映了该图像中不同灰度级出现的统计情况。图2给出了一个直方图的示例，其中图(a)是一幅图像，其灰度直方图可表示为图(b)，其中横轴表示图像的各灰度级，纵轴表示图像中各灰度级像素的个数。（需要注意，灰度直方图表示了在图像中各个单独灰度级的分布，而图像对比度则取决于相邻近像素之间灰度级的关系。）
f f f的归一化直方图定义为： p ( r k ) = h ( r k ) / M N = n k / M N p(r_k) = h(r_k)/MN=n_k/MN p(rk)=h(rk)/MN=nk/MN
其中M和N分别是图像的行数和列数。
通常将归一化直方图简称为直方图。
对k的所有值， p ( r k ) p(r_k) p(rk)的和总是1，也就是MN=这幅L级灰度数字图像 f ( x , y ) f(x,y) f(x,y)的像素和。
事实上， p ( r k ) p(r_k) p(rk)就是对图像中出现的灰度级的概率的估计。
3.1、直方图均衡化
介绍：直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。
原理：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。
理论基础
一个相关结论：
1.灰度连续
变换函数：
结论： p s ( s ) p_s(s) ps(s)是一个均匀的密度函数
2.灰度离散
变换函数：
实例：
我们生活中常常遇到的是离散型的。
3.1、直方图匹配（规定化）
从上面可以看出，直方图的均衡化自动的确定了变换函数，可以很方便的得到变换后的图像，且结果可以预知，但是在有些应用中这种自动的增强并不是最好的方法。有时候，需要图像具有某一特定的直方图形状（也就是灰度分布），而不是均匀分布的直方图，这时候可以使用直方图规定化。
步骤：
