智能优化算法:蝗虫优化算法-附代码
智能优化算法:蝗虫优化算法-附代码
文章目录
- 智能优化算法:蝗虫优化算法-附代码
-
- 1.算法原理
- 2.算法流程
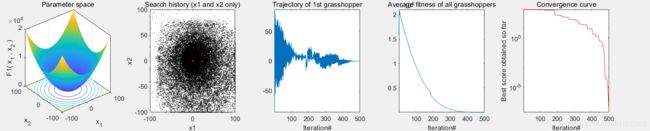
- 3.算法结果
- 4.参考文献:
- 5.matlab代码:
- 6.python代码:
摘要:蝗虫算法( Grasshopper Optimization Algorithm,GOA ) 是 由 Saremi 等[1]于2017 年提出的一种元启发式仿生优化算法,具有较高的搜索效率和较快的收敛速度,且算法本身特殊的自适应机制能够很好地平衡全局和局部搜索过程,具有较好的寻优精度。
1.算法原理
根据蝗虫算法模拟蝗虫在自然界中的种群迁移和觅食行为将搜索分为: 探索和开发。对该过程进行数学建模,蝗虫算法的数学公式如下:
X i = S i + G i + A i X_{i}=S_{i}+G_{i}+A_{i} Xi=Si+Gi+Ai
式中: X i X_{i} Xi为第 i i i 个蝗虫的位置; S i S_{i} Si为个体间相互影响力; G i G_{i} Gi为第 i i i 个蝗虫受到的重力; A i A_{i} Ai为第 i i i 个蝗虫受到的风力。蝗虫的社会作用对蝗虫位置的影响最大。 S i S_{i} Si计算如下:
S i = ∑ j = 1 , j ≠ i N s ( d i j ) d i j S_{i}=\sum_{j=1,j\neq i}^{N}s(d_{ij})\bold{d_{ij}} Si=j=1,j=i∑Ns(dij)dij
式中: d i j = ∣ x i − x j ∣ d_{ij} = |x_{i}-x_{j}| dij=∣xi−xj∣为第 i 个蝗虫与第 j 个蝗虫之间的距离; d i j = ( x j − x i ) / d i j \bold{d_{ij}}=(x_{j}-x{i})/d_{ij} dij=(xj−xi)/dij为第 i 个蝗虫指向第 j 个蝗虫的单位向量; s 为社会力量,其为负数时表示相互排斥,为正数时表示相互吸引,计算方法如下:
s = f e − r l − e − r s=fe^{\frac {-r}{l}}-e^{-r} s=fel−r−e−r
式中: f f f 为吸引强度; l l l 为吸引长度尺度。当 l = 1.5 , f = 0.5 l=1. 5,f= 0. 5 l=1.5,f=0.5 时,函数$ s$ 的曲线显示了蝗虫之间的相互作用力( 吸引和排斥)。
由图 1 可知,在区间( 1. 000,2. 079) 内,存在排斥力; 当距离等于 2. 079 时,即没有吸引力也没有排斥力,称这一区域为舒适区; 当距离从 2. 079 增加到4.000 的过程中,存在吸引 力,且开始 是 逐 渐 增加的,然后吸引力逐渐减少。改变式中的$ f$ 和 l l l 参数时,蝗虫之间的相互力会改变,如图 2 所示。根据图 2 中的函数曲线,选择参数 l = 1.5 , f = 0.5 l=1. 5,f=0. 5 l=1.5,f=0.5
可以直观地显示蝗虫之间相对于舒适区域的相互作用的概念性示意图如图 3 所示。函数 s s s 存在一个不足,即当蝗虫之间的距离过大时作用力将不存在,因此要将蝗虫之间的距离做标准化处理。
G i G_{i} Gi可计算如下:
G i = − g e g G_{i}=-ge_{g} Gi=−geg
式中: g g g 为重力常数; e g e_{g} eg为指向地球中心的单位向量。
A i A_{i} Ai可计算如下:
A i = u e w A_{i}=ue_{w} Ai=uew
式中: u u u 为风力常量; e w e_{w} ew为指向风向的单位向量。于是 X i X_{i} Xi可表示为:
X i = ∑ j = 1 , j ≠ i N s ( ∣ x j − x i ∣ ) x j − x i d i j − g e g + u e w X_{i}=\sum_{j=1,j\neq i}^{N}s(|x_{j}-x{i}|)\frac {x_{j}-x_{i}}{d_{ij}}-ge_{g}+ue_{w} Xi=j=1,j=i∑Ns(∣xj−xi∣)dijxj−xi−geg+uew
通常当蝗虫群到达舒适区时,虫群仍旧没有收敛,为了适应优化问题的求解,协调全局和局部优化过程,通过引入参数以区分不同阶段的寻优。改进后的数学模型如下:
X i = ∑ j = 1 , j ≠ i N c u b d − l b d 2 s ( ∣ x j − x i ∣ ) x j − x i d i j + T d X_{i}=\sum_{j=1,j\neq i}^{N}c\frac {ub_{d}-lb_{d}}{2}s(|x_{j}-x{i}|)\frac {x_{j}-x_{i}}{d_{ij}}+T_{d} Xi=j=1,j=i∑Nc2ubd−lbds(∣xj−xi∣)dijxj−xi+Td
式中: c c c 为递减系数,决定着舒适区、斥力区和吸引区的大小; N N N 为蝗虫数量; u b d ub_{d} ubd和 l b d lb_{d} lbd分别为函数 s ( r ) = f e − r l − e − r s(r)=fe^{\frac {-r}{l}}-e^{-r} s(r)=fel−r−e−r在 d d d 维空间上的上下界; T d T_{d} Td为目前为止蝗虫位置在 d d d 维空间上的最佳解。式中不考虑重力影响,且假定风向总指向最优解。内部的 c c c 有助于减少蝗虫之间的斥力或吸引力,且与迭代次数成正比,外部的 c c c 随着迭代次数
的增加会减少对目标周围的搜索区域。利用下式(更新参数 c c c,随着迭代次数的增加,减少全局搜索,并增加局部精度搜索。
c = c m a x − n c m a x − c m i n L c = c_{max}-n\frac {c_{max}-c_{min}}{L} c=cmax−nLcmax−cmin
式中: c m a x c_max cmax为最大值; c m i n c_min cmin为最小值; n n n 为当前迭代次数; L L L 为 最 大 迭 代 次 数; 本 文 取 c m a x = 1 , c m i n = 0.00004 c_{max}= 1,c_{min}=0.00004 cmax=1,cmin=0.00004。
2.算法流程
算法步骤如下:
( 1) 初始化。首先初始化蝗虫种群 和算法中各参数。
( 2) 计算每个蝗虫的适应度;
( 3) 计算当前最佳适应度;
( 4) 判断是否达到迭代次数,若达到,则程序结束,当前的全局最优解的位置即为最优解
( 5) 更新参数 c;
( 6) 标准化蝗虫之间的距离,归一化区间为[1,4];
( 7) 更新蝗虫的位置,并计算更新后的蝗虫适应度,与历史最佳进行比较,若适应度优于历史最佳,则更新,否则不更新;
( 8) 更新迭代次数,并返回到( 4)
3.算法结果
4.参考文献:
[1]Shahrzad Saremi,Seyedali Mirjalili,Andrew Lewis. Grasshopper Optimisation Algorithm: Theory and application[J]. Advances in Engineering Software,2017,105.
[2]程泽新,李东生,高杨.基于蝗虫算法的无人机三维航迹规划[J].飞行力学,2019,37(02):46-50+55.
5.matlab代码:
https://mianbaoduo.com/o/bread/mbd-Z5ealZ0=
文献复现代码
[1]赵然,郭志川,朱小勇.一种基于Levy飞行的改进蝗虫优化算法[J].计算机与现代化,2020(01):104-110.
https://mianbaoduo.com/o/bread/mbd-YZaUlZZy
[1]李洋州,顾磊.基于曲线自适应和模拟退火的蝗虫优化算法[J].计算机应用研究,2019,36(12):3637-3643.
https://mianbaoduo.com/o/bread/mbd-YZaUlZ1w
[1]何庆,林杰,徐航.混合柯西变异和均匀分布的蝗虫优化算法[J/OL].控制与决策:1-10[2021-01-08].https://doi.org/10.13195/j.kzyjc.2019.1609.
https://mianbaoduo.com/o/bread/YZaUlpZp
6.python代码:
https://mianbaoduo.com/o/bread/YZmXmJ9w