*用python实现改遗传算法解柔性作业车间调度问题的完整编码(用8*8和mk01做测例)(改进版本)
GA主程序:
import numpy as np
import random
from Decode_for_FJSP import Decode
from Encode_for_FJSP import Encode
import itertools
import matplotlib.pyplot as plt
class GA:
def __init__(self):
self.Pop_size=300 #种群数量
self.P_c=0.8 #交叉概率
self.P_m=0.3 #变异概率
self.P_v=0.5 #选择何种方式进行交叉
self.P_w=0.95 #采用何种方式进行变异
self.Max_Itertions=50 #最大迭代次数
#适应度
def fitness(self,CHS,J,Processing_time,M_num,Len):
Fit=[]
for i in range(len(CHS)):
d = Decode(J, Processing_time, M_num)
Fit.append(d.Decode_1(CHS[i],Len))
return Fit
#机器部分交叉
def Crossover_Machine(self,CHS1,CHS2,T0):
T_r=[j for j in range(T0)]
r = random.randint(1, 10) # 在区间[1,T0]内产生一个整数r
random.shuffle(T_r)
R = T_r[0:r] # 按照随机数r产生r个互不相等的整数
# 将父代的染色体复制到子代中去,保持他们的顺序和位置
OS_1=CHS1[T0:2*T0]
OS_2 = CHS2[T0:2 * T0]
C_1 = CHS2[0:T0]
C_2 = CHS1[0:T0]
for i in R:
K,K_2 = C_1[i],C_2[i]
C_1[i],C_2[i] = K_2,K
CHS1=np.hstack((C_1,OS_1))
CHS2 = np.hstack((C_2, OS_2))
return CHS1,CHS2
#工序交叉部分
def Crossover_Operation(self,CHS1, CHS2, T0, J_num):
OS_1 = CHS1[T0:2 * T0]
OS_2 = CHS2[T0:2 * T0]
MS_1 =CHS1[0:T0]
MS_2 = CHS2[0:T0]
Job_list = [i for i in range(J_num)]
random.shuffle(Job_list)
r = random.randint(1, J_num - 1)
Set1 = Job_list[0:r]
Set2 = Job_list[r:J_num]
new_os = list(np.zeros(T0, dtype=int))
for k, v in enumerate(OS_1):
if v in Set1:
new_os[k] = v + 1
for i in OS_2:
if i not in Set1:
Site = new_os.index(0)
new_os[Site] = i + 1
new_os = np.array([j - 1 for j in new_os])
CHS1=np.hstack((MS_1,new_os))
CHS2 = np.hstack((MS_2, new_os))
return CHS1,CHS2
def reduction(self,num,J,T0):
T0=[j for j in range(T0)]
K=[]
Site=0
for k,v in J.items():
K.append(T0[Site:Site+v])
Site+=v
for i in range(len(K)):
if num in K[i]:
Job=i
O_num=K[i].index(num)
break
return Job,O_num
#机器变异部分
def Variation_Machine(self,CHS,O,T0,J):
Tr=[i_num for i_num in range(T0)]
MS=CHS[0:T0]
OS=CHS[T0:2*T0]
# 机器选择部分
r = random.randint(1, T0 - 1) # 在变异染色体中选择r个位置
random.shuffle(Tr)
T_r = Tr[0:r]
for i in T_r:
Job=self.reduction(i,J,T0)
O_i=Job[0]
O_j =Job[1]
Machine_using = O[O_i][O_j]
Machine_time = []
for j in Machine_using:
if j != 9999:
Machine_time.append(j)
Min_index = Machine_time.index(min(Machine_time))
MS[i] = Min_index
CHS=np.hstack((MS,OS))
return CHS
#工序变异部分
def Variation_Operation(self, CHS,T0,J_num,J,Processing_time,M_num):
MS=CHS[0:T0]
OS=list(CHS[T0:2*T0])
r=random.randint(1,J_num-1)
Tr=[i for i in range(J_num)]
random.shuffle(Tr)
Tr=Tr[0:r]
J_os=dict(enumerate(OS)) #随机选择r个不同的基因
J_os = sorted(J_os.items(), key=lambda d: d[1])
Site=[]
for i in range(r):
Site.append(OS.index(Tr[i]))
A=list(itertools.permutations(Tr, r))
A_CHS=[]
for i in range(len(A)):
for j in range(len(A[i])):
OS[Site[j]]=A[i][j]
C_I=np.hstack((MS,OS))
A_CHS.append(C_I)
Fit = []
for i in range(len(A_CHS)):
d = Decode(J, Processing_time, M_num)
Fit.append(d.Decode_1(CHS, T0))
return A_CHS[Fit.index(min(Fit))]
def Select(self,Fit_value):
Fit=[]
for i in range(len(Fit_value)):
fit=1/Fit_value[i]
Fit.append(fit)
Fit=np.array(Fit)
idx = np.random.choice(np.arange(len(Fit_value)), size=len(Fit_value), replace=True,
p=(Fit) / (Fit.sum()))
return idx
def main(self,Processing_time,J,M_num,J_num,O_num):
e = Encode(Processing_time, self.Pop_size, J, J_num, M_num)
OS_List=e.OS_List()
Len_Chromo=e.Len_Chromo
CHS1=e.Global_initial()
CHS2 = e.Random_initial()
CHS3 = e.Local_initial()
C=np.vstack((CHS1,CHS2,CHS3))
Optimal_fit=9999
Optimal_CHS=0
x = np.linspace(0, 50, 50)
Best_fit=[]
for i in range(self.Max_Itertions):
Fit = self.fitness(C, J, Processing_time, M_num, Len_Chromo)
Best = C[Fit.index(min(Fit))]
best_fitness = min(Fit)
if best_fitness < Optimal_fit:
Optimal_fit = best_fitness
Optimal_CHS = Best
Best_fit.append(Optimal_fit)
print('best_fitness', best_fitness)
d = Decode(J, Processing_time, M_num)
Fit.append(d.Decode_1(Optimal_CHS, Len_Chromo))
d.Gantt(d.Machines)
else:
Best_fit.append(Optimal_fit)
Select = self.Select(Fit)
for j in range(len(C)):
offspring = []
if random.random()>>>>',len(Crossover[0]),len(Crossover[1]))
else:
Crossover=self.Crossover_Operation(C[j],C[N_i],Len_Chromo,J_num)
offspring.append(Crossover[0])
offspring.append(Crossover[1])
offspring.append(C[j])
if random.random() Encode类
import numpy as np
import random
class Encode:
def __init__(self,Matrix,Pop_size,J,J_num,M_num):
self.Matrix=Matrix #工件各工序对应各机器加工时间矩阵
self.GS_num=int(0.6*Pop_size) #全局选择初始化
self.LS_num=int(0.2*Pop_size) #局部选择初始化
self.RS_num=int(0.2*Pop_size) #随机选择初始化
self.J=J #各工件对应的工序数
self.J_num=J_num #工件数
self.M_num=M_num #机器数
self.CHS=[]
self.Len_Chromo=0
for i in J.values():
self.Len_Chromo+=i
#生成工序准备的部分
def OS_List(self):
OS_list=[]
for k,v in self.J.items():
OS_add=[k-1 for j in range(v)]
OS_list.extend(OS_add)
return OS_list
#生成初始化矩阵
def CHS_Matrix(self, C_num): # C_num:所需列数
return np.zeros([C_num, self.Len_Chromo], dtype=int)
def Site(self,Job,Operation):
O_num = 0
for i in range(len(self.J)):
if i == Job:
return O_num + Operation
else:
O_num = O_num + self.J[i + 1]
return O_num
#全局选择初始化
def Global_initial(self):
MS=self.CHS_Matrix(self.GS_num)
OS_list= self.OS_List()
OS=self.CHS_Matrix(self.GS_num)
for i in range(self.GS_num):
Machine_time = np.zeros(self.M_num, dtype=float) # 机器时间初始化
random.shuffle(OS_list) # 生成工序排序部分
OS[i] = np.array(OS_list)
GJ_list = [i_1 for i_1 in range(self.J_num)]
random.shuffle(GJ_list)
for g in GJ_list: # 随机选择工件集的第一个工件,从工件集中剔除这个工件
h = self.Matrix[g] # 第一个工件含有的工序
for j in range(len(h)): # 从工件的第一个工序开始选择机器
D = h[j]
List_Machine_weizhi = []
for k in range(len(D)): # 每道工序可使用的机器以及机器的加工时间
Useing_Machine = D[k]
if Useing_Machine != 9999: # 确定可加工该工序的机器
List_Machine_weizhi.append(k)
Machine_Select = []
for Machine_add in List_Machine_weizhi: # 将这道工序的可用机器时间和以前积累的机器时间相加
# 比较可用机器的时间加上以前累计的机器时间的时间值,并选出时间最小
Machine_Select.append(Machine_time[Machine_add] + D[
Machine_add])
Min_time = min(Machine_Select)
K = Machine_Select.index(Min_time)
I = List_Machine_weizhi[K]
Machine_time[I] += Min_time
site=self.Site(g,j)
MS[i][site] = K
CHS1 = np.hstack((MS, OS))
return CHS1
#局部选择初始化
def Local_initial(self):
MS = self.CHS_Matrix(self.LS_num)
OS_list = self.OS_List()
OS = self.CHS_Matrix(self.LS_num)
for i in range(self.LS_num):
random.shuffle(OS_list) # 生成工序排序部分
OS_gongxu = OS_list
OS[i] = np.array(OS_gongxu)
GJ_list = [i_1 for i_1 in range(self.J_num)]
for g in GJ_list:
Machine_time = np.zeros(self.M_num) # 机器时间初始化
h =self.Matrix[g] # 第一个工件及其对应工序的加工时间
for j in range(len(h)): # 从工件的第一个工序开始选择机器
D = h[j]
List_Machine_weizhi = []
for k in range(len(D)): # 每道工序可使用的机器以及机器的加工时间
Useing_Machine = D[k]
if Useing_Machine == 9999: # 确定可加工该工序的机器
continue
else:
List_Machine_weizhi.append(k)
Machine_Select = []
for Machine_add in List_Machine_weizhi: # 将这道工序的可用机器时间和以前积累的机器时间相加
Machine_time[Machine_add] = Machine_time[Machine_add] + D[
Machine_add] # 比较可用机器的时间加上以前累计的机器时间的时间值,并选出时间最小
Machine_Select.append(Machine_time[Machine_add])
Machine_Index_add = Machine_Select.index(min(Machine_Select))
site = self.Site(g, j)
MS[i][site] = MS[i][site] + Machine_Index_add
CHS1 = np.hstack((MS, OS))
return CHS1
def Random_initial(self):
MS = self.CHS_Matrix(self.RS_num)
OS_list = self.OS_List()
OS = self.CHS_Matrix(self.RS_num)
for i in range(self.RS_num):
random.shuffle(OS_list) # 生成工序排序部分
OS_gongxu = OS_list
OS[i] = np.array(OS_gongxu)
GJ_list = [i_1 for i_1 in range(self.J_num)]
A = 0
for gon in GJ_list:
Machine_time = np.zeros(self.M_num) # 机器时间初始化
g = gon # 随机选择工件集的第一个工件 #从工件集中剔除这个工件
h = np.array(self.Matrix[g]) # 第一个工件及其对应工序的加工时间
for j in range(len(h)): # 从工件的第一个工序开始选择机器
D = np.array(h[j])
List_Machine_weizhi = []
Site=0
for k in range(len(D)): # 每道工序可使用的机器以及机器的加工时间
if D[k] == 9999: # 确定可加工该工序的机器
continue
else:
List_Machine_weizhi.append(Site)
Site+=1
Machine_Index_add = random.choice(List_Machine_weizhi)
MS[i][A] = MS[i][A] + Machine_Index_add
A += 1
CHS1 = np.hstack((MS, OS))
return CHS1
Decode类:
import matplotlib.pyplot as plt
from Jobs import Job
from Machines import Machine_Time_window
import numpy as np
class Decode:
def __init__(self,J,Processing_time,M_num):
self.Processing_time = Processing_time
self.Scheduled = [] # 已经排产过的工序
self.M_num = M_num
self.Machines = [] # 存储机器类
self.fitness = 0
self.J=J #
for j in range(M_num):
self.Machines.append(Machine_Time_window(j))
self.Machine_State = np.zeros(M_num, dtype=int) # 在机器上加工的工件是哪个
self.Jobs = [] #存储工件类
for k, v in J.items():
self.Jobs.append(Job(k, v))
#时间顺序矩阵和机器顺序矩阵
def Order_Matrix(self,MS):
JM=[]
T=[]
Ms_decompose=[]
Site=0
for S_i in self.J.values():
Ms_decompose.append(MS[Site:Site+S_i])
Site+=S_i
for i in range(len(Ms_decompose)):
JM_i=[]
T_i=[]
for j in range(len(Ms_decompose[i])):
O_j=self.Processing_time[i][j]
M_ij=[]
T_ij=[]
for Mac_num in range(len(O_j)): # 寻找MS对应部分的机器时间和机器顺序
if O_j[Mac_num] != 9999:
M_ij.append(Mac_num)
T_ij.append(O_j[Mac_num])
else:
continue
JM_i.append(M_ij[Ms_decompose[i][j]])
T_i.append(T_ij[Ms_decompose[i][j]])
JM.append(JM_i)
T.append(T_i)
return JM,T
def Earliest_Start(self,Job,O_num,Machine):
P_t=self.Processing_time[Job][O_num][Machine]
last_O_end = self.Jobs[Job].Last_Processing_end_time # 上道工序结束时间
Selected_Machine=Machine
M_window = self.Machines[Selected_Machine].Empty_time_window()
M_Tstart = M_window[0]
M_Tend = M_window[1]
M_Tlen = M_window[2]
Machine_end_time = self.Machines[Selected_Machine].End_time
ealiest_start = max(last_O_end, Machine_end_time)
if M_Tlen is not None: # 此处为全插入时窗
for le_i in range(len(M_Tlen)):
if M_Tlen[le_i] >= P_t:
if M_Tstart[le_i] >= last_O_end:
ealiest_start=M_Tstart[le_i]
break
if M_Tstart[le_i] < last_O_end and M_Tend[le_i] - last_O_end >= P_t:
ealiest_start = last_O_end
break
M_Ealiest = ealiest_start
End_work_time = M_Ealiest + P_t
return M_Ealiest, Selected_Machine, P_t, O_num,last_O_end,End_work_time
#解码
def Decode_1(self,CHS,Len_Chromo):
MS=list(CHS[0:Len_Chromo])
OS=list(CHS[Len_Chromo:2*Len_Chromo])
Needed_Matrix=self.Order_Matrix(MS)
JM=Needed_Matrix[0]
for i in OS:
Job=i
O_num=self.Jobs[Job].Current_Processed()
Machine=JM[Job][O_num]
Para=self.Earliest_Start(Job,O_num,Machine)
self.Jobs[Job]._Input(Para[0],Para[5],Para[1])
if Para[5]>self.fitness:
self.fitness=Para[5]
self.Machines[Machine]._Input(Job,Para[0],Para[2],Para[3])
return self.fitness
def Gantt(self,Machines):
M = ['red', 'blue', 'yellow', 'orange', 'green', 'palegoldenrod', 'purple', 'pink', 'Thistle', 'Magenta',
'SlateBlue', 'RoyalBlue', 'Cyan', 'Aqua', 'floralwhite', 'ghostwhite', 'goldenrod', 'mediumslateblue',
'navajowhite',
'navy', 'sandybrown', 'moccasin']
for i in range(len(Machines)):
Machine=Machines[i]
Start_time=Machine.O_start
End_time=Machine.O_end
for i_1 in range(len(End_time)):
# plt.barh(i,width=End_time[i_1]-Start_time[i_1],height=0.8,left=Start_time[i_1],\
# color=M[Machine.assigned_task[i_1][0]],edgecolor='black')
# plt.text(x=Start_time[i_1]+0.1,y=i,s=Machine.assigned_task[i_1])
plt.barh(i, width=End_time[i_1] - Start_time[i_1], height=0.8, left=Start_time[i_1], \
color='white', edgecolor='black')
plt.text(x=Start_time[i_1] + (End_time[i_1] - Start_time[i_1])/2-0.5, y=i, s=Machine.assigned_task[i_1][0])
plt.yticks(np.arange(i + 1), np.arange(1, i + 2))
plt.title('Scheduling Gantt chart')
plt.ylabel('Machines')
plt.xlabel('Time(s)')
plt.show()
Job类:
class Job:
def __init__(self,Job_index,Operation_num):
self.Job_index=Job_index
self.Operation_num = Operation_num
self.Processed=[]
self.Last_Processing_end_time=0
self.J_start=[]
self.J_end=[]
self.J_machine=[]
self.J_worker=[]
self.Last_Processing_Machine=None
def Current_Processed(self):
return len(self.Processed)
def _Input(self,W_Eailiest,End_time,Machine):
self.Processed.append(1)
self.Last_Processing_Machine=Machine
self.Last_Processing_end_time=End_time
self.J_start.append(W_Eailiest)
self.J_end.append(End_time)
self.J_machine.append(Machine)
Machine类:
class Machine_Time_window:
def __init__(self,Machine_index):
self.Machine_index=Machine_index
self.assigned_task = []
self.worker_for_task=[]
self.O_start = []
self.O_end = []
self.End_time=0
#机器的哪些时间窗是空的,此处只考虑内部封闭的时间窗
def Empty_time_window(self):
time_window_start = []
time_window_end = []
len_time_window=[]
if self.O_end is None:
pass
elif len(self.O_end)==1:
if self.O_start[0]!=0:
time_window_start=[0]
time_window_end=[self.O_start[0]]
elif len(self.O_end)>1:
if self.O_start[0] !=0:
time_window_start.append(0)
time_window_end.append(self.O_start[0])
time_window_start.extend(self.O_end[:-1]) #因为使用时间窗的结束点就是空时间窗的开始点
time_window_end.extend(self.O_start[1:])
if time_window_end is not None:
len_time_window=[time_window_end[i]-time_window_start[i] for i in range(len(time_window_end))]
return time_window_start,time_window_end,len_time_window
def Machine_Burden(self):
if len(self.O_start)==0:
burden=0
else:
processing_time=[self.O_end[i]-self.O_start[i] for i in range(len(self.O_start))]
burden=sum(processing_time)
return burden
def _Input(self,Job,M_Ealiest,P_t,O_num):
if self.O_end!=[]:
if self.O_start[-1]>M_Ealiest:
for i in range(len(self.O_end)):
if self.O_start[i]>=M_Ealiest:
self.assigned_task.insert(i,[Job + 1, O_num + 1])
break
else:
self.assigned_task.append([Job+1,O_num+1])
else:
self.assigned_task.append([Job+1,O_num+1])
self.O_start.append(M_Ealiest)
self.O_start.sort()
self.O_end.append(M_Ealiest+P_t)
self.O_end.sort()
self.End_time=self.O_end[-1]测例(8*8):
import numpy as np
Processing_time=[[[5, 3, 5, 3, 3, 9999, 10, 9],
[10, 9999, 5, 8, 3, 9, 9, 6],
[9999, 10, 9999, 5, 6, 2, 4, 5]],
[[5, 7, 3, 9, 8, 9999, 9, 9999],
[9999, 8, 5, 2, 6, 7, 10, 9],
[9999, 10, 9999, 5, 6, 4, 1, 7],
[10, 8, 9, 6, 4, 7, 9999, 9999]],
[[10, 9999, 9999, 7, 6, 5, 2, 4],
[9999, 10, 6, 4, 8, 9, 10, 9999],
[1, 4, 5, 6, 9999, 10, 9999, 7]],
[[3, 1, 6, 5, 9, 7, 8, 4],
[12, 11, 7, 8, 10, 5, 6, 9],
[4, 6, 2, 10, 3, 9, 5, 7]],
[[3, 6, 7, 8, 9, 9999, 10, 9999],
[10, 9999, 7, 4, 9, 8, 6, 9999],
[9999, 9, 8, 7, 4, 2, 7, 9999],
[11, 9, 9999, 6, 7, 5, 3, 6]],
[[6, 7, 1, 4, 6, 9, 9999, 10],
[11, 9999, 9, 9, 9, 7, 8, 4],
[10, 5, 9, 10, 11, 9999, 10, 9999]],
[[5, 4, 2, 6, 7, 9999, 10, 9999],
[9999, 9, 9999, 9, 11, 9, 10, 5],
[9999, 8, 9, 3, 8, 6, 9999, 10]],
[[2, 8, 5, 9, 9999, 4, 9999, 10],
[7, 4, 7, 8, 9, 9999, 10, 9999],
[9, 9, 9999, 8, 5, 6, 7, 1],
[9, 9999, 3, 7, 1, 5, 8, 9999]]]
J={1:3,2:4,3:3,4:3,5:4,6:3,7:3,8:4}
M_num=8
O_Max_len=4
J_num=8
O_num=27
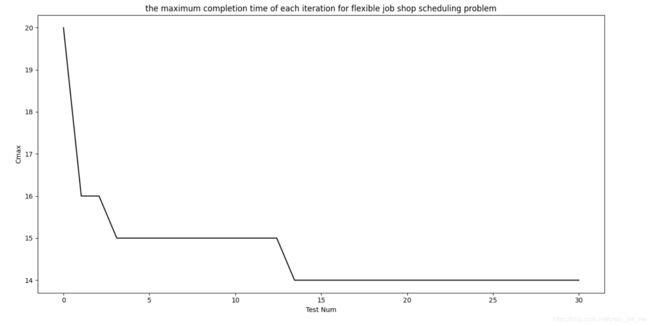
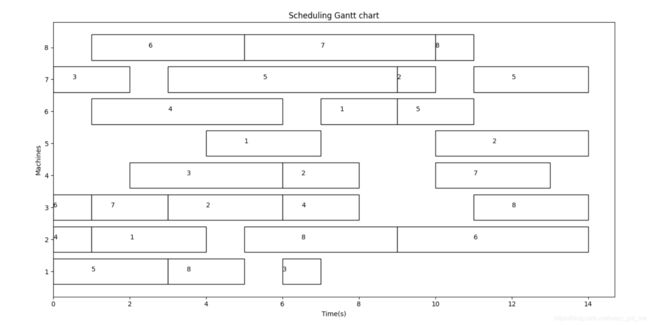
(8*8)测例结果
测例mk01:
Processing_time=[[[5, 9999, 4, 9999, 9999, 9999],
[9999, 1, 5, 9999, 3, 9999],
[9999, 9999, 4, 9999, 9999, 2],
[1, 6, 9999, 9999, 9999, 5],
[9999, 9999, 1, 9999, 9999, 9999],
[9999, 9999, 6, 3, 9999, 6]],
[[9999, 6, 9999, 9999, 9999, 9999],
[9999, 9999, 1, 9999, 9999, 9999],
[2, 9999, 9999, 9999, 9999, 9999],
[9999, 6, 9999, 6, 9999, 9999],
[1, 6, 9999, 9999, 9999, 5]],
[[9999, 6, 9999, 9999, 9999, 9999],
[9999, 9999, 4, 9999, 9999, 2],
[1, 6, 9999, 9999, 9999, 5],
[9999, 6, 4, 9999, 9999, 6],
[1, 9999, 9999, 9999, 5, 9999]],
[[1, 6, 9999, 9999, 9999, 5],
[9999, 6, 9999, 9999, 9999, 9999],
[9999, 9999, 1, 9999, 9999, 9999],
[9999, 1, 5, 9999, 3, 9999],
[9999, 9999, 4, 9999, 9999, 2]],
[[9999, 1, 5, 9999, 3, 9999],
[1, 6, 9999, 9999, 9999, 5],
[9999, 6, 9999, 9999, 9999, 9999],
[5, 9999, 4, 9999, 9999, 9999],
[9999, 6, 9999, 6, 9999, 9999],
[9999, 6, 4, 9999, 9999, 6]],
[[9999, 9999, 4, 9999, 9999, 2],
[2, 9999, 9999, 9999, 9999, 9999],
[9999, 6, 4, 9999, 9999, 6],
[9999, 6, 9999, 9999, 9999, 9999],
[1, 6, 9999, 9999, 9999, 5],
[3, 9999, 9999, 2, 9999, 9999]],
[[9999, 9999, 9999, 9999, 9999, 1],
[3, 9999, 9999, 2, 9999, 9999],
[9999, 6, 4, 9999, 9999, 6],
[6, 6, 9999, 9999, 1, 9999],
[9999, 9999, 1, 9999, 9999, 9999]],
[[9999, 9999, 4, 9999, 9999, 2],
[9999, 6, 4, 9999, 9999, 6],
[1, 6, 9999, 9999, 9999, 5],
[9999, 6, 9999, 9999, 9999, 9999],
[9999, 6, 9999, 6, 9999, 9999]],
[[9999, 9999, 9999, 9999, 9999, 1],
[1, 9999, 9999, 9999, 5, 9999],
[9999, 9999, 6, 3, 9999, 6],
[2, 9999, 9999, 9999, 9999, 9999],
[9999, 6, 4, 9999, 9999, 6],
[9999, 6, 9999, 6, 9999, 9999]],
[[9999, 9999, 4, 9999, 9999, 2],
[9999, 6, 4, 9999, 9999, 6],
[9999, 1, 5, 9999, 3, 9999],
[9999, 9999, 9999, 9999, 9999, 1],
[9999, 6, 9999, 6, 9999, 9999],
[3, 9999, 9999, 2, 9999, 9999]]]
L=0
O_num=55
M_num=6
J_num=10
J={1:6,2:5,3:5,4:5,5:6,6:6,7:5,8:5,9:6,10:6}
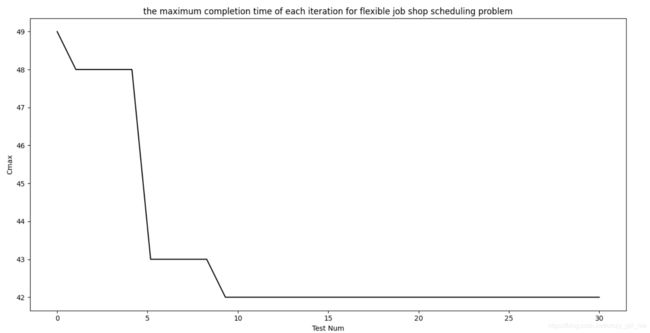
mk01结果: