根据PyTorch学习CONV1D

新手刚学习卷积，不知道理解的有没有问题，如果有问题劳烦大家指出。

1. PyTorch中的torch.nn.Conv1d()函数

官方文档链接

torch.nn.Conv1d(in_channels, 
				out_channels, 
				kernel_size, 
				stride=1, 
				padding=0, 
				dilation=1, 
				groups=1, 
				bias=True, 
				padding_mode='zeros')

作用是Applies a 1D convolution over an input signal composed of several input planes.
首先要明确CONV1D和一维卷积（1D convolution）并不是一个概念。

参数：

• in_channels (int) – 输入图片的通道数量。在文本分类中，即为词向量的维度
• out_channels (int) – 卷积产生的通道。有多少个out_channels，就需要多少个1维卷积
• kernel_size (int or tuple) – 卷积核的尺寸，卷积核的大小为(k,)，第二个维度是由in_channels来决定的，所以实际上卷积核大小为kernel_size*in_channels
• stride (int or tuple, optional) – 卷积步长， Default: 1
• padding (int or tuple, optional) – 输入的每一条边补充0的层数，Default: 0
• padding_mode (string, optional) – ‘zeros’, ‘reflect’, ‘replicate’ or ‘circular’. Default: ‘zeros’
• dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1
• groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1
  groups参数控制输入和输出的连接。
  当groups = 2时，这个操作相当于有两个conv层并排，每个conv层看到一半的输入通道，产生一半的输出通道，然后两者concate起来。
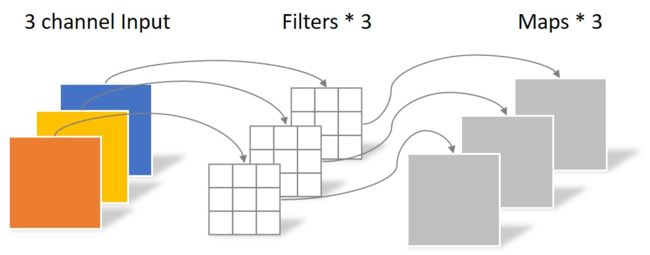
  当groups = in_channels 并且out_channels = K * in_channels, K是一个正整数, 就得到了 “depthwise convolution”.
  下图是一个图像的depthwise convolution的示例
  详见：卷积神经网络中的Separable Convolution
  
• bias (bool, optional) – If True, adds a learnable bias to the output. Default: True

在最简单的情况下，输入维度为$(N,C_{in},L_{in})$，输出维度为$(N,C_{out},L_{out})$

• N:batch size
• C表示通道数量
• L是信号序列的长度
• ⋆ 表示做互相关函数（cross-correlation）计算

这个公式看着非常的抽象，暂且放在一边。
先来观察输入输出，不考虑代表batch size的N
那么输入为一个$(C_{in},L_{in})$大小的矩阵，输出为$(C_{out},L_{out})$大小的矩阵
其中$L_{out}$的大小可以根据输入大小和卷积核的参数来确定。

通俗地说，$L_{out}$代表一个filter能在输入中滑动多少次。
再看一下weight的维度

out_channels应该表示有out_channels个的卷积核，暂且设groups为1，即一个卷积核要处理输入的所有通道。那么卷积核的尺寸为$(C_{in},kerne{l}_{s}ize)$
再来看离散信号的互相关函数计算公式：

看了Weight的size和互相关函数的公式，再回头去看公式，就能大致了解了。
然后我将CONV1D的计算画成了一张图：

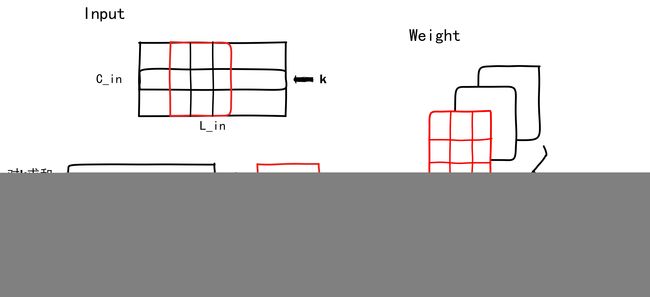
下面来对上图做一些说明，暂时不考虑batch size，先设batch size = 1
Weight中存放了$C_{out}$个卷积核，对应了$C_{out}$个输出的feature map
每一个卷积核的kernel_size是我们定义的，卷积核的另一个维度为输入通道数$C_{in}$
我们先来看一个输出的feature map如何计算

• 先取一个卷积核Weight[j,:,:]，让其在输入数据中“滑动”，它能“滑动”多少次，决定了输出的序列长度。
• 输入矩阵的第k行和卷积核的第k行做互相关的计算，这个计算，就好似卷积核不断移动，与输入对应位置的元素做对应元素逐个相乘并求和。
• 最后要纵向看，输入的每一个通道与卷积核的相应行卷积出的向量（序列）要加在一起，也就是公式中对k做的求和。

代码示例

import torch
import torch.nn as nn

# 输入通道大小为16， 输出通道大小为33， kernel_size为3， 步长为2
m = nn.Conv1d(16, 33, 3, stride=2)
# 输入数据，假设batch_size为20， 输入通道数为16， 序列长度为50
input = torch.randn(20, 16, 50)
# 根据公式可计算出输出序列长度（50-1x(3-1)-1)/2 + 1 = 24
output = m(input) # 20, 33, 24

2. 使用Conv1d()对文本进行卷积

下面这个例子来自斯坦福cs224n 2019年的课件
CS224N Winter 2019

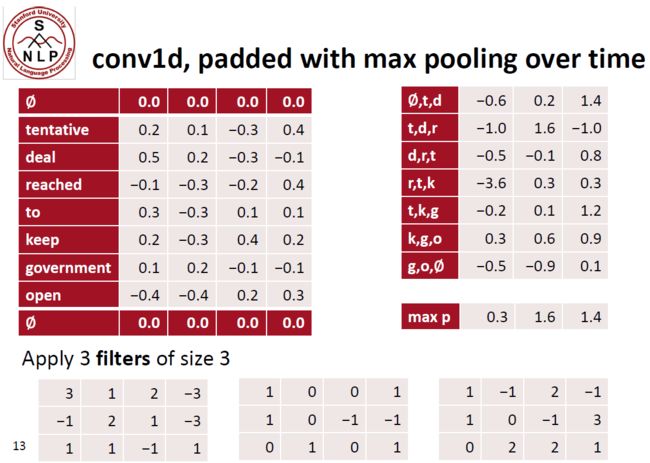
PyTorch实现

import torch
import torch.nn as nn

batch_size = 16
word_embed_size = 4     # embedding维度，对应输入通道数量
seq_len = 7    			# 句子长度，对应输入序列长度

input = torch.randn(batch_size, word_embed_size, seq_len)
conv1 =  torch.nn.Conv1d(in_channels=word_embed_size,
					     out_channels=3,
						 kernel_size=3,
					 	 padding = 1)
hidden1 = conv1(input)   #torch.Size([16, 3, 7])
# max pooling
hidden2 = torch.max(hidden1, dim=2)