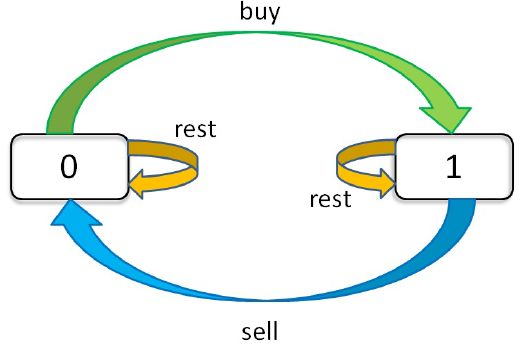
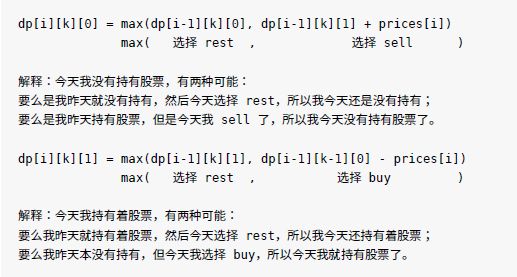
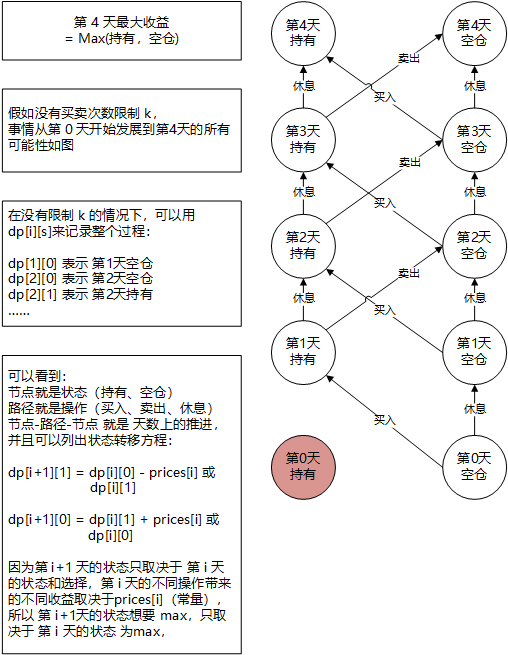
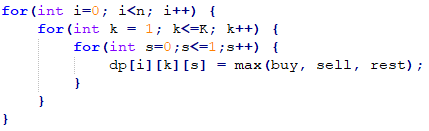用状态机的技巧(不要害怕,其实就是DP table)来解决股票买卖问题,可以全部提交通过。
leetcode 买卖股票的最佳时机的 6 道题是有共性的,看下 IV 题,是最泛化的形式,其他的问题都是这个形式的简化:
第 I 题是只进行一次交易, 相当于 k = 1;
第 II 题是不限交易次数,相当于 k = +INF;
第 III 题是只进行2次交易,相当于 k = 2;
剩下两道题也是不限次数,但是加了交易 「冷冻期」和「⼿续费」的额外条件,其实就是第二题的变种,都很容易处理。
一、穷举框架
如何穷举?穷举和递归的思想不太一样。递归其实是符合我们思考的逻辑的:一步步推进,遇到无法解决的就丢给递归,一不小心就做出来,可读性还很好。缺点就是一旦出错,也不容易找到错误出现的原因。
这里我们利用「状态」进⾏穷举。具体到每一天,看看总共有几种可能的「状态」,再找出每个「状态」对应的选择,穷举的目的是根据对应的「选择」更新状态。
比如这个问题,每天都有三种「选择」:买入(buy)、卖出(sell)、无操作(rest)。但这三种选择不是相互独立的:sell 必须在 buy 之后。并且操作还应该分两种状态,一种是未持有(0)的操作,一种是已持有(1)后的操作。并且,剩余可交易次数 k 还限制 buy 只能在 k>0 的前提下操作。
这个问题的「状态」有三个: 第⼀个是天数;第⼆个是允许交易的最⼤次数;第三个是当前的持有状态( 1 表⽰持有,0 表⽰空仓),然后我们用一个三维数组就可以 装下下面这几种状态的全部组合:
dp[3][2][1] 的含义:今天是第三天,现在手上持有股票,最多允许2次交易。
我们想求的最终答案是dp[n-1][K][0],即最后一天,最多允许K次交易,最多获得多少利润。[0] 表示最终不持有股票,当然比持有股票利润更大。
二、状态转移框架
我们已经完成了「状态」的穷举,现在思考每种「状态」有哪些「选择」,应该如何更新「状态」。
如果 buy,就要从利润中减去 prices[i],如果 sell,就要给利润增加 prices[i]。并且注意 k 的限制,我们在选择 buy 的时候,把 k 减小 1,相当于剩下可用的交易次数少 1。
(如果 k 代表当前允许交易次数的话,随着买入操作,k应该减小,是买入导致了k减小,所以应该是 dp[i][k-1][l] = dp[i-1][k][0] - prices[i];而此处 k 代表当前已进行的交易次数,所以随着买入操作,k会增大。两种理解都可以,就是状态转移方程和base case 里面涉及k的对应修改一下。作者这里的解释和他给的状态转移方程对不上,读者不必纠结,按这两种k的理解写出自己的状态转移方程和base case 即可)
这里需要做出更详细的解释。假设 i = 5,那么我们着手画出它的状态转移图:
好吧,画不下去了。
原因是:第4天到底是卖出、买入还是休息,取决于目前是否已经持有股票,所以这里分化出了两棵树:一棵是当前持有,一棵是当前空仓。
而第4天是否持有股票又取决于第3天的持有状态及操作。
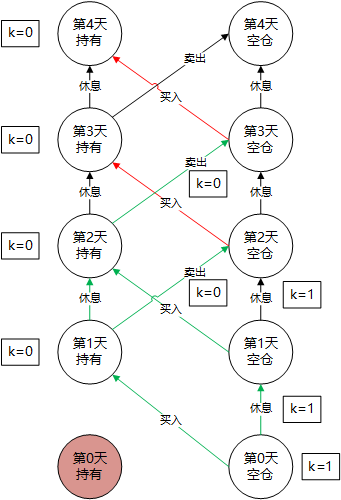
当没有买卖次数的限制条件时,上图的每条路径都可以走,但当有了买卖次数限制条件 k 时,每做 1 次买卖(假设买时记 k-1,卖时k不变),k 将减少 1,直到 k=0 时,允许的可买卖次数用尽,后面的买路径就不能再走了,如下图所示,假如走了绿色的路径,那红色的路径就因为k=0不能再买入而走不通了:
(注意,这里的 k 表示当前允许的最大买卖次数)
那么 k 的加入相当于帮我们剪掉了某些路径,一旦 k = 0,就不能再进行买入操作。所以我们每次操作选择后,还需要维护 k 的状态,但选择不同的路径,会获得不同的 k 值,也就是 :
dp[0][0] 第0天,空仓,对应一个 k值为1,
dp[1][0] 第1天,空仓,对应一个k值为1,
dp[1][1] 第1天,持有,对应一个k值为0,
dp[2][0] 第2天,空仓,这里就有两种可能,
如果dp[2][0] = dp[1][1] + prices[1],说明第一天持有并卖出,k = 0
如果dp[2][0] = dp[1][0],说明第一天空仓并休息,k=1
所以 k 与 dp[i][s] 是多对一关系,且范围在 [0,k] 波动,所以这些可能性需要新开一个维度来记录,现在dp[i][s] 扩展到了 dp[i][k][s],那么 dp[i][0][s] 代表 k=0时的dp[i][s]值,而 dp[i][1][s] 代表 k=1时的值。这里不太容易理解,也就是数组下标对应了 k 的取值,刚好数组下标不能小于0。
现在,我们已经完成了动态规划中最困难的一步:状态转移方程。下面就要定义base case了:
(作者这里的解释不对, k=0意味着不允许交易,但不是利润为0的原因,虽然不允许交易,但可以继承前面几天的利润对吧?这里利润为0是因为,他定义的 k=0 其实是当前已交易次数,最大交易次数是1,已交易次数为0,说明没有交易过 ,利润当然是0;而dp[i][0][1] = -infinity 也不是因为不允许交易的情况下不可能持有股票,因为可以继承过去买入的股票,虽然不能买入但一直没有卖出,也是持有股票的对吧?作者定义的 k=0其实是当前已交易次数,当前已交易次数为0说明不可能已经买入,所以不可能持有。)
把上面的状态转移方程总结一下:
三、题目实战
1. 第 I 题,k = 1
k=1 即只允许买卖一次,状态转移方程如下(注意作者的 k 表示当前已交易次数):
(第 i 天,空仓)的状态,可以从(第 i-1 天,空仓,第 i 天休息)、(第 i-1天,持有,第i 天卖出)这两种途径达到。
(第 i 天,持有)的状态,可以从(第i-1天,持有,第 i 天休息)、(第 i-1 天,空仓,第 i 天买入)这两种途径达到。
化简后发现 k 都是 1,即对状态转移方程没有影响,可以进一步简化:
写出代码:
dp[n-1][0] 就是最后一天,空仓时的总收益。
但 i=0 时, dp[i-1] 是越界的,所以还要对base case 进行处理。
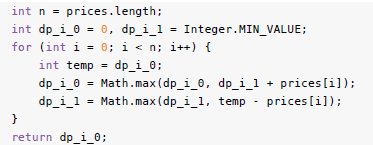
注意今天的状态只依赖于昨天的状态,所以用不上整个dp 数组,只需要两个变量来更新每天的持有、空仓两个状态即可。
2. 第 II 题,k = +INF
·如果 k 为正无穷,可以认为 k 和 k-1是一样的,可以这样改写状态转移方程:
代码如下:
3. 最佳买卖股票时机含冷冻期 ,k = + INF with cooldown
每次卖出后,要等一天才能继续交易,只要把这个特点融入上一题的状态转移方程即可:
代码:
4. 最佳买卖股票时机含手续费,k = + INF with fee
每次交易要支付手续费,只要把手续费从利润中减去即可。
代码:
5. 第 III 题,k = 2
由于没有消除 k的影响,所以必须对 k 进行穷举(循环):
其实这里有点问题,max_k 不一定 小于 n,假如只有2天,max_k = 3,这样会产生非常多的无效计算:
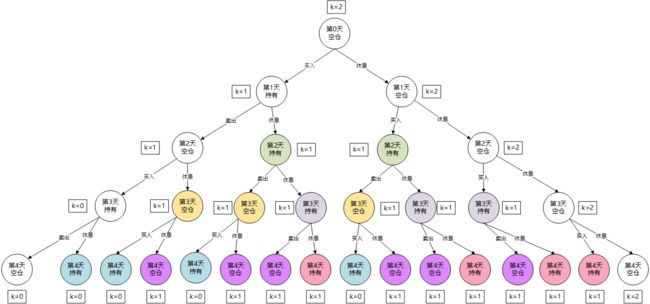
当然这种穷举不是每个 dp[i][k][s] 都有意义,比如 dp[0][1][s] 代表第0天只允许再交易1次,但这样的节点是不可能存在的,一开始允许的交易最大次数是2次;再者,dp[1][0][s] 也是不可能存在的,因为刚过去一天,不可能交易次数就减少了2。(如下图示 i、k与作者的设定不同,i =0 表示还未开始,i=1才表示第一天,k=2表示还未买入,k=0表示已买过2次,允许购买次数为0)
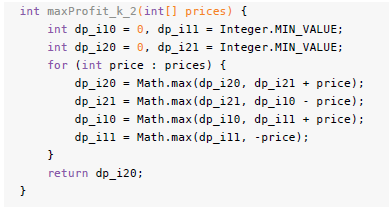
由于 k 的取值范围比较小,这里还可以直接把 k=1和 k=2的情况全部列出来:
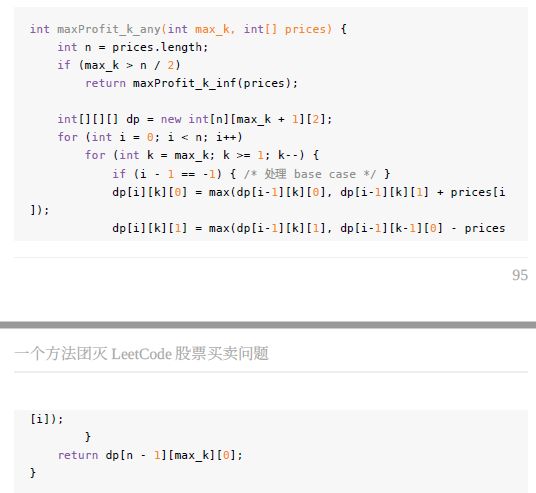
6. 第 IV 题,K = 给定
有了 K=2 的铺垫,这题解法应该和上一题没什么区别,但会超内存。其实有效的 K 不应该超过 n/2,更进一步地,在穷举过程中,如果 k 表示已交易次数, k应该 不大于 i/2,因为每两天最多交易一次;如果 k表示当前最大可交易数,K - k < i/2。
这里代码只处理了宏观的情况,即给定的 K 不应超过 n/2 的情况,直接当成K=INF 来调用了前面的代码:
四、总结
用一个状态转移方程完成了 6 道股票买卖问题,其实不难,但这已经属于动态规划问题中较困难的了,我们发现了三个状态,使用了一个三维数组,可以说是三维DP问题了,但解法无非还是穷举 + 更新。
关键就在于列出所有可能的「状态」,然后想想怎么穷举更新这些「状态」。一般用一个多维 dp 数组存储这些状态,从 base case 开始向后推进,推进道最后的状态,就是我们想要的答案。
作者这part写得不是很好,他的思路和如下差不多,但没写清楚,有疑惑的朋友可以看下面的(leetcode @千万利器莫过于信念):