数据元素: 既对象,如用户,商品
数据项: 描述数据元素的维度,如id,name
数据对象: 数据元素的集合
一:数据
1.逻辑结构
指数据元素之间的关系.
- 集合结构: 描述数据元素之间的共同性,等同于数学上的集合.
- 线性结构: 描述数据元素之间具有唯一性的一对一关系,线形的.
- 树形结构: 描述元素之间的层级关系.
- 图形结构: 描述元素之间的不唯一的一对一关系,网状的.
2.物理结构
指元素在内存中的物理地址之间的关系.
- 顺序存储: 数据对象的元素存储在一段连续的物理地址中,数据结构直接映射到物理地址.
- 链式存储: 数据结构映射到一组指针上,数据元素可任意存储在其他位置.
3.数据类型
- 原子类型: 不可分割的基础数据类型,比如整形,实数型,字符型,布尔型等
- 结构类型: 由多个原子型自定义组合成的类型,比如结构体,集合等
- 抽象类型: 不仅仅可以是原子或者结构类型,甚至可以是非数学的,可以是复杂的结构,用来描述对象,比如定义一个向量,有长度和方向;或者定义一只猫的行为,跑,睡,吃等.
二:算法
1.特性
- 输入和输出: 输入是可选的,但是算法一定有输出.
- 有穷性: 算法必须能够在合适的时间内自动结束,一定能走到末尾不能无限循环.
- 确定性: 算法的每一步都必须有唯一的目的,相同的输入需要有相同的目标结果(这个结果并一定指输出的值,而是要符合设计的结果,因为可能有随机的过程存在)
- 可行性: 算法要能在指定的机器上运行.
2.目标
算法是解决问题的方法,并且不是唯一的,因此就有优劣之分;
因此好的算法追求正确性、可读性、健壮性、高效率;
3.算法的效率
预估一个算法的效率,最基础的就是判断这个算法中计算机基本操作的执行次数.
但是除此之外还得考虑输入规模,随着输入规模的增大,基本操作的执行次数(操作规模)的增大幅度越小,算法效率越高.
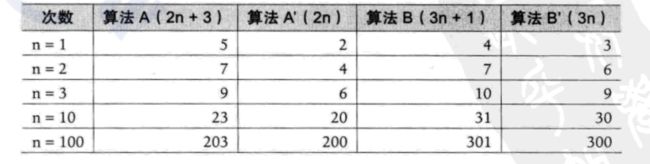
忽略定义,打印等其他操作,当输入规模是n时,算法一的操作规模是n,所以f(n) = n;而算法二的操作规模仍然是1,因此f(n) = 1.
对于这个函数f(n),放几个图感受一下:
当然了,具体情况具体考虑,算法还是需要考虑输入规模的,但是多数情况下,随着输入规模的增长,操作规模的增长总是指数>倍数>常数.
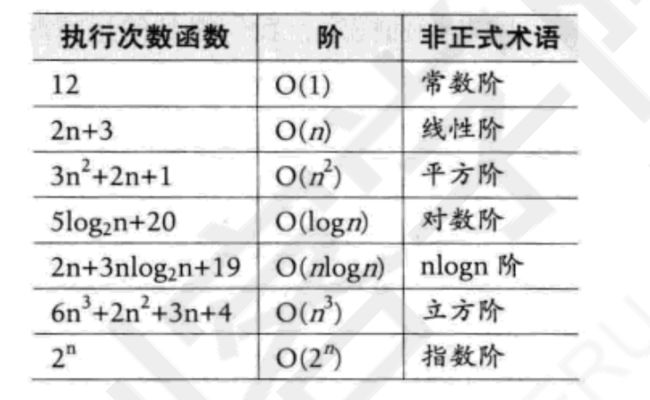
4.时间复杂度
不管输入规模是多少,总是执行固定次数的部分,叫做常数阶;相同速度增长的叫做线性阶,以此类推还可以有平方阶等等;
使用O来表示时间复杂度,流程如下
- 先看有没有最高阶,如果有,只保留最高阶,并且去掉最高阶的系数.
-
如果没有高阶,常数阶不管执行多少次,固定写作1;
也就是说,没有O(2),O(2n),O(n+1),O(n^2+3n)等等这些表示.
看几个例子:
这个循环的次数不是n,每次循环count都是x2,因此当2的x次方时,大于n,循环结束,x = log2n,时间复杂度为O(logn)
时间复杂度O(n^2),如果是j 执行函数是n + (n-1) + (n-2) + ... + 1 = n^2 / 2 + n / 2; 保留最高阶,去掉系数,最终时间复杂度是O(n^2) 以上算法都有循环,经常用在查找案例上,并且是按照循环全走完的情况来计算时间复杂度,也就是说最后一个才是要找到对象,这种叫做最坏时间复杂度,除此之外还有平均时间复杂度. 做几个题: 简化为i2 = n,要执行i=根号n次,复杂度为O(√n) 假设第x次结束,则2x = n,则x=log2n,这个2是系数,不管是2还是345都不影响复杂度,因此复杂度为O(logn) 第一层循环n次,第二层最多循环n次,第三层也一样,直接就O(n^3) 循环n+(n-2)+(n-4)+...+0 = ((n/2 + 1)*(n+0))2次,结果是O(n^2) 5.算法的空间复杂度
i只能等于1,2,4,...2n,同时i就等于内层循环的次数,因此f(N) = 1+2+4+...+2
n,可以认为最终i=N,也就是2n=N,则n=log2N,那么f(N) = 1(1-2^(log2N)) / (1-2) = N-1;因此复杂度为O(n)
指算法执行过程中占用的存储资源.
例如计算一个公元元年到公元2050年之间的年份是否为闰年,可以先存好这2050个结果,0或者1,之后这个问题就变成了获取数组指定位置的元素.
空间复杂度的计算方法是S(n) = O(f(n)),n是问题规模,f(n)是空间占用函数.