【MATLAB】极坐标绘图 ( Polar Chart 极坐标图 | MATLAB 绘图问题 1 )
文章目录
- 一、Polar Chart 极坐标图问题
- 二、Polar Chart 极坐标图
一、Polar Chart 极坐标图问题
应一位博客粉丝提出的问题 , 给出 MATLAB 绘图方案 ;
绘图样式 :
二、Polar Chart 极坐标图
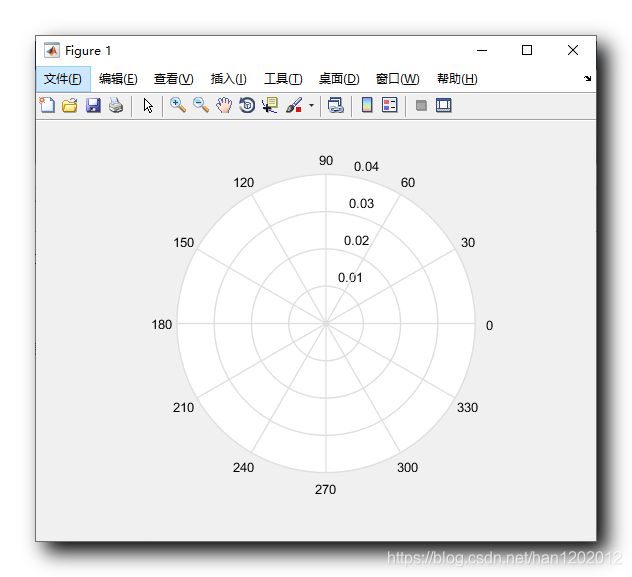
首先极坐标范围是 0 0 0 ~ 0.04 0.04 0.04 , 绘制的第一个曲线 , 先标定范围 , 用于限定最大值 ;
% 绘制极坐标图, 设置极坐标的最大值范围
polar(0, 0.04);
当前绘制效果 : 仅用于限定坐标系范围
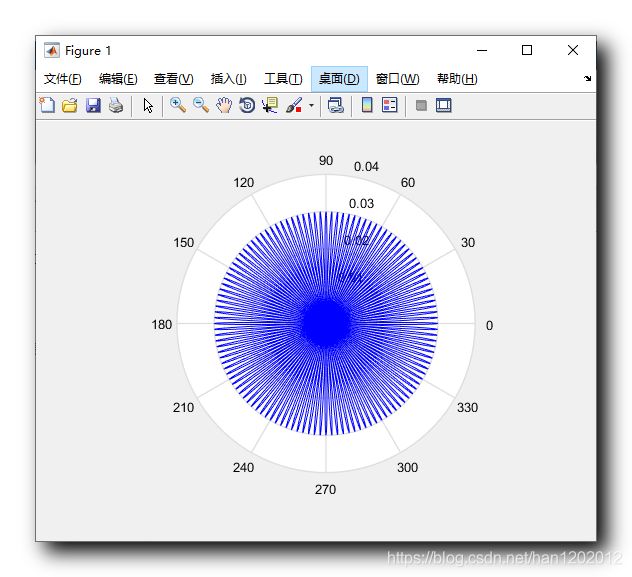
绘制内层稀疏曲线 :
为了使曲线看起来更加平滑 , 这里设置角度采样的个数 100000 100000 100000 , 样本个数越多 , 曲线越平滑 ,
半径向量值直接图中是 0.03 0.03 0.03 , 直接使用该向量值 ;
将两个曲线绘制在一个极坐标系中 , 这样需要在两个 polar 函数之间使用
hold on;
代码 ;
设置曲线绘制颜色在 polar 函数中 , 第三个参数使用 'b' 指定 , 绘制曲线是蓝色的 ;
polar(theta, r, 'b');
当前阶段代码 :
% 角度值向量
theta = linspace(0, 2 * pi, 100000);
% 半径值向量
r = 0.03 * cos(60 * theta);
% 绘制极坐标图, 设置极坐标的最大值范围
polar(0, 0.04);
hold on;
% 绘制内层图像
polar(theta, r, 'b');
当前绘制效果 :
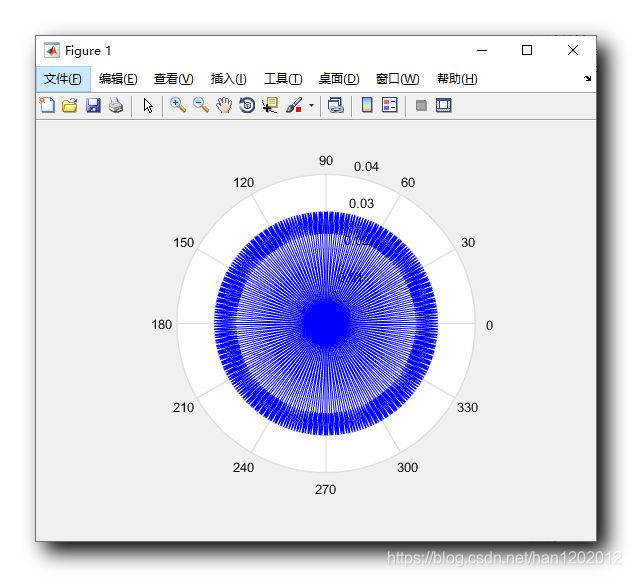
绘制外层密集曲线 :
外层曲线的角度值范围也是 0 0 0 ~ 2 π 2 \pi 2π ,
只是半径的向量在 0.027 0.027 0.027 ~ 0.03 0.03 0.03 之间 , 这里直接使用 0.027 + 0.03 × cos ( 250 ∗ t h e t a 1 ) 0.027 + 0.03 \times \cos(250 * \rm theta1) 0.027+0.03×cos(250∗theta1) 获得 , 设置 250 250 250 是因为需要获得更加密集的曲线坐标点 ;
% 角度值向量
theta1 = linspace(0, 2 * pi, 100000);
% 半径值向量
r1 = 0.027+ 0.003 * cos(250 * theta1);
将两个曲线绘制在一个极坐标系中 , 这样需要在两个 polar 函数之间使用
hold on;
代码 ;
设置曲线绘制颜色在 polar 函数中 , 第三个参数使用 'b' 指定 , 绘制曲线是蓝色的 ;
polar(theta1, r1, 'b');
完整绘图代码 :
% 角度值向量
theta = linspace(0, 2 * pi, 100000);
% 半径值向量
r = 0.03 * cos(60 * theta);
% 角度值向量
theta1 = linspace(0, 2 * pi, 100000);
% 半径值向量
r1 = 0.027+ 0.003 * cos(250 * theta1);
% 绘制极坐标图, 设置极坐标的最大值范围
polar(0, 0.04);
hold on;
% 绘制内层图像
polar(theta, r, 'b');
hold on;
% 绘制外层图像
polar(theta1, r1, 'b');
如果要求改绘图的曲线密度 , 修改
% 半径值向量
r = 0.03 * cos(60 * theta);
和
% 半径值向量
r1 = 0.027+ 0.003 * cos(250 * theta1);
中 cos \cos cos 函数内的值 , 即 60 60 60 和 250 250 250 这两个值 ;